Kapitel
- Algebraische Ausdrücke
- Monome
- Rechenoperationen mit Monomen
- Produkt aus einer Zahl und einem Monom
- Polynome
- Grad eines Polynoms
- Vollständiges Polynom
- Geordnetes Polynom
- Gleiche Polynome
- Zahlenwert eines Polynoms
- Rechenoperationen mit Polynomen
- Division von Polynomen
- Horner-Schema
- Binomische Formeln
- Faktorisierung eines Polynoms
- Methoden zur Faktorisierung eines Polynoms
- Bruchterme
- Äquivalente Bruchterme
- Rechnen mit Bruchtermen
Algebraische Ausdrücke
In der Algebra geht es um den Umgang mit numerischen Relationen, bei denen eine oder mehrere Größen unbekannt sind. Diese Größen heißen Variablen oder Unbekannte und werden als Buchstaben dargestellt.
Ein algebraischer Ausdruck ist eine Kombination aus Buchstaben und Zahlen mit entsprechenden Zeichen der durchzuführenden Rechenoperationen: Addition, Subtraktion, Multiplikation, Division und Potenzierung.
Zahlenwert
Der Zahlenwert eines algebraischen Ausdrucks ist die Zahl, die man erhält, wenn man die gleichen Buchstaben durch bestimme Zahlen ersetzt und die gegebenen Rechenoperationen durchführt.
Monome
Ein Monom ist ein algebraischer Ausdruck, bei dem die einzigen Rechenoperationen, die zwischen den Variablen auftauchen, das Produkt und die Potenz des natürlichen Exponenten sind.
Der Koeffizient des Monoms ist die Zahl, die mit den Variablen multipliziert wird.
Die Variable besteht aus Buchstaben und deren Exponenten.
Der Grad des Monoms ist die Summe aller Exponenten der Buchstaben oder Variablen.
Zwei Monome sind gleichartig, wenn sie die gleiche Variable haben.
Rechenoperationen mit Monomen
Summe von Monomen
Wir können nur gleichartige Monome addieren.
Die Summe der Monome ist ein weiteres Monom, das die gleiche Variable hat und dessen Koeffizient die Summe der Koeffizienten ist.
Produkt aus einer Zahl und einem Monom
Das Produkt aus einer Zahl und einem Monom ist ein weiteres gleichartiges Monom, dessen Koeffizient das Produkt aus dem Koeffizienten und der Zahl ist.
Produkte aus Monomen
Das Produkt aus Monomen ist ein weiteres Produkt, dessen Koeffizient das Produkt aus den Koeffizienten ist und dessen Variable man erhält, indem man die Potenzen mit der gleichen Basis addiert.
Quotient aus Monomen
Der Quotient aus Monomen ist ein weiteres Monom, dessen Koeffizient der Quotient aus den Koeffizienten ist und dessen Variable man erhält, indem man die Potenzen mit der gleichen Basis subtrahiert.
Polynome
Ein Polynom ist ein algebraischer Ausdruck der folgenden Form:
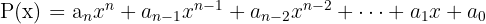
Da 
Zahlen sind, nennt man sie Koeffizienten.
ist eine natürliche Zahl.
ist die Variable oder Unbekannte.
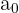ist das konstante Glied.
Grad eines Polynoms
Der Grad eines Polynoms 
ist der höchste Exponent der Variablen ..
Vollständiges Polynom
Ein vollständiges Polynom hat alle Glieder, vom konstanten Glied bis zum Term mit dem höchsten Grad
Geordnetes Polynom
Ein Polynom ist geordnet, wenn die Monome, aus denen das Polynom besteht, nach absteigendem Grad sortiert sind.
Gleiche Polynome
Zwei Polynome sind gleich, wenn:
Sie haben den gleichen Grad.
Die Koeffizienten der Terme mit dem gleichen Grad sind gleich.
Zahlenwert eines Polynoms
Ist das Ergebnis, das wir erhalten, wenn wir die Variable latex]x[/latex] durch irgendeine Zahl ersetzen.
Rechenoperationen mit Polynomen
Summe von Polynomen
Um zwei Polynome zu addieren, werden die Koeffizienten der Terme mit dem gleichen Grad addiert.
Der Unterschied besteht darin, das Gegenteil des Subtrahenden zu addieren.
Multiplikation von Monomen
Produkt aus einer Zahl und einem Polynom
Das Ergebnis ist ein weiteres Polynom, das den gleichen Grad wie das Polynom hat und dessen Koeffizient das Produkt aus den Koeffizienten des Polynoms und der Zahl ist.
Produkt aus einem Monom und einem Polynom
Das Monom wird mit jedem einzelnen Monom, aus dem das Polynom besteht, multipliziert.
Produkt aus Polynomen
1 Jedes Monom des ersten Polynoms wird mit allen Elementen des zweiten Polynoms multipliziert.
2 Monome vom gleichen Grad werden zusammengefasst.
Division von Polynomen
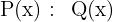
Auf der linken Seite steht der Dividend. Falls das Polynom nicht vollständig ist, lassen wir an den entsprechenden Stellen eine Lücke.
Der Divisor steht in einer Klammer auf der rechten Seite.
Wir dividieren das erste Monom des Dividenden durch das erste Monom des Divisors.
Wir multiplizieren jeden Term des Polynoms des Divisors durch das vorher erhaltene Ergebnis und subtrahieren es vom Polynom des Dividenden:
Wir dividieren noch einmal das erste Polynom des Dividenden durch das erste Monom des Divisors. Das Ergebnis multiplizieren wir mit dem Divisor und subtrahieren es vom Dividenden.
Diese Vorgehensweise wiederholen wir so lange, bis der Grad der Differenz niedriger als der Grad des Divisors ist. Danach können wir auch nicht weiter dividieren.
Um zu sehen, ob wir richtig gerechnet haben, überprüfen wir wie folgt:
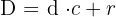
Horner-Schema
Wenn der Divisor eines Polynoms in der Form x — a auftaucht, können wir eine vereinfachte Methode für die Division anwenden: das Horner-Schema.
1 Wenn das Polynom nicht vollständig ist, vervollständigen wir es, indem wir für die fehlenden Terme 0 einsetzen.
2 Wir schreiben die Koeffizienten in eine Zeile.
3 Eine Zeile darunter schreiben wir nach links das konstante Glied des Divisors mit umgekehrtem Vorzeichen.
4 Wir ziehen einen Strich und schreiben den ersten Koeffizienten darunter.
5 Wir multiplizieren diesen Koeffizienten mit dem Divisor und schreiben ihn unter den darauffolgenden Term.
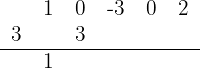
6 Wir addieren die beiden Koeffizienten.
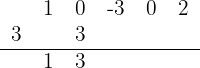
7 Wir wiederholen die Schritte 5 und 6 so oft wie nötig.
8 Die letzte Zahl, die wir erhalten, ist der Rest.
9 Der Quotient ist ein Polynom, dessen Grad um 1 niedriger ist als der des Dividenden. Die Koeffizienten sind die, die wir erhalten haben.
Binomische Formeln
Ein Binom zum Quadrat
Summe mal Differenz
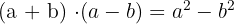
Ein Binom zum Kubik
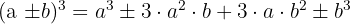
Faktorisierung eines Polynoms
Restsatz
Der Rest, der bei der Division eines Polynoms , durch ein Polynom der Form 
bleibt, ist der Zahlenwert des besagten Polynoms für den Wert: 
.
Faktorsatz
Das Polynom ist teilbar durch ein Polynom der Form , aber nur wenn gilt: 
.
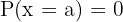Der Wert für heißt Nullstelle von .
Beobachtungen
1 Die Nullstellen sind Teiler des konstanten Glieds des Polynoms.
2 Zu jeder Nullstelle vom Typ gehört ein Binom vom Typ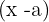 
.
3 Wir können ein Polynom faktorisieren, indem wir es als Produkt aus allen Binomen der Form schreiben. Für die zu berechnenden Nullstellen gilt .
4 Die Summe der Exponenten der Binome muss dem Grad der Polynome entsprechen.
5 Jedes Polynom ohne konstantes Glied hat eine Nullstelle bei 
oder als Faktor, was das Gleiche ist.
6 Ein Polynom heißt irreduzibel, wenn es nicht in Faktoren zerlegt werden kann.
Methoden zur Faktorisierung eines Polynoms
Den gemeinsamen Faktor ausklammern
Anwendung des Distributivgesetzes.
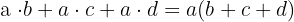
Subtraktion von quadratischen Ausdrücken
Die Subtraktion von quadratischen Ausdrücken entspricht dem Produkt aus Summe und Differenz.
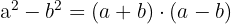
Perfektes quadratisches Trinom
Ein perfektes quadratisches Trinom ist ein Binom zum Quadrat.
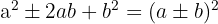
Trinom zweiten Grades
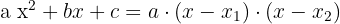
Polynom mit einem höheren Grad als zwei.
Wir wenden den Restsatz und das Horner-Schema an.
1 Wir nehmen die Teiler des konstanten Glieds: 
.
2 Durch die Anwendung des Restsatzes wissen wir, für welche Werte bei der Division kein Rest bleibt.
3 Dividieren mit dem Horner-Schema.
4 Da die Division aufgeht, gilt 
5 Wir führen die gleichen Rechenschritte beim zweiten Faktor durch, solange bis wir den Grad 1 erhalten oder nicht weiter in reelle Faktoren zerlegen können.
Bruchterme
Ein Bruchterm ist der Quotient zweier Polynome und wird wie folgt dargestellt:
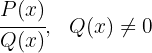
ist der Zähler und
ist der Nenner.
Äquivalente Bruchterme
Zwei Bruchterme
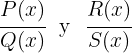
sind äquivalent und werden wie folgt dargestellt:
wenn gilt: 
.
Gegeben ist ein Bruchterm. Wenn wir den Zähler und den Nenner mit dem selben Polynom, das größer als 0 ist, multiplizieren, ist der resultierende Bruchterm äquivalent zum gegebenen Bruchterm.
Vereinfachung von Bruchtermen
Um Bruchterme zu vereinfachen, teilt man den Zähler und den Nenner des Bruchterms durch ein Polynom, das ein gemeinsamer Faktor von beiden ist.
Bruchterme mit gemeinsamem Nenner kürzen
Gegeben sind zwei Bruchterme. Um beide auf einen gemeinsamen Nenner zu bringen, muss man zwei äquivalente Bruchterme mit demselben Nenner finden.
1 Wir zerlegen die Nenner in Faktoren, um das kleinste gemeinsame Vielfache der Nenner zu bestimmen. Dies ist dann der gemeinsame Nenner.
2 Wir teilen den gemeinsamen Nenner durch die Nenner der gegebenen Bruchterme und multiplizieren das Ergebnis mit dem entsprechenden Zähler.
Rechnen mit Bruchtermen
Addition und Subtraktion von Bruchtermen
Bruchterme mit gleichem Nenner
Die Summe von Bruchtermen mit dem gleichen Nenner ist ein weiterer Bruchterm mit dem gleichen Nenner und dessen Zähler die Summe der Zähler ist.
Bruchterme mit unterschiedlichem Nenner
Als Erstes werden die Bruchterme auf einen gemeinsamen Nenner gebracht. Danach werden die Zähler addiert.
Produkt aus Bruchtermen
Das Produkt aus zwei Bruchtermen ist ein weiterer Bruchterm, bei dem der Zähler das Produkt aus den Zählern und der Nenner das Produkt aus den Nennern ist.
Quotient aus Bruchtermen
Der Quotient aus zwei Bruchtermen ist ein weiterer Bruchterm. Der Zähler ist hierbei das Produkt aus dem Zähler des ersten Bruchterms und dem Nenner des zweiten Bruchterms. Der Nenner ist hierbei das Produkt aus dem Nenner des Ersten und dem Zähler des Zweiten.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
