Kapitel

Faktorregel
Eine Polynomfunktion  ist nur dann durch ein Polynom der Form
ist nur dann durch ein Polynom der Form 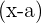 teilbar , wenn
teilbar , wenn  gleich Null oder die Wurzel von
gleich Null oder die Wurzel von  ist.
ist.
Wurzeln einer Polynomfunktion
Die Wurzeln (oder Nullstellen) eines Polynoms sind die Werte, durch die sich das Polynom aufheben lässt, daher ist ihr Wert gleich Null, d.h.  ist eine Nullstelle von
ist eine Nullstelle von  , wenn
, wenn  .
.
Beispiel:
Überprüfe, ob 2 und 3 Nullstellen der Polynomfunktion 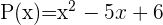 sind.
sind.
1 Setze 2 und 3 in die Funktion  ein und ermittle, ob das Ergebnis gleich Null ist.
ein und ermittle, ob das Ergebnis gleich Null ist.
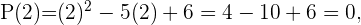

2 Daraus lässt sich schließen, dass 2 und 3 Nullstellen der Polynomfunktion  sind.
sind.
Eigenschaften von Nullstellen und Faktoren einer Polynomfunktion
1Die Nullstellen (oder Wurzeln) einer Polynomfunktion sind Teiler des konstanten Glieds des Polynoms.
Beispiel:
Die möglichen Nullstellen der Funktion [Latex]{P(x) = x^2-6x + 8}[/latex] sind Teiler von 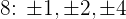 und
und 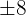 .
.
Durch Einsetzen der möglichen Nullstellen in die Funktion erkennt man, dass 2 und 4 die einzigen Werte sind, die Null als Ergebnis liefern
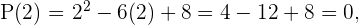
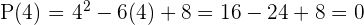
Daraus lösst sich schließen, dass 2 und 4 die Nullstellen der Polynomfunktion  sind.
sind.
2Jeder Nullstelle der Form  entspricht ein Binom der Form
entspricht ein Binom der Form 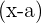 .
.
Beispiel:
Für  ist das entsprechende Binom
ist das entsprechende Binom 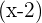 .
.
Für 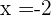 ist das entsprechende Binom
ist das entsprechende Binom  .
.
3Eine Polynomfunktion kann durch Faktoren ausgedrückt werden, und zwar als Produkt aller Binome der Form 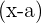 für die möglichen Nullstellen
für die möglichen Nullstellen  .
.
Beispiel

4Der Grad einer Polynomfunktion entspricht immer der Summe aller Exponenten.
Beispiele:

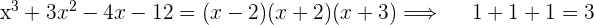
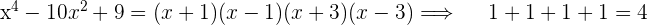
5Polynomfunktionen, die kein konstantes Glied enthalten, haben als Nullstelle  , bzw. können mit Faktor
, bzw. können mit Faktor  ausgedrückt werden.
ausgedrückt werden.
Beispiel
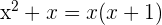
Wurzeln:  y
y 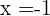
6Ein Polynom wird als irreduzibel (oder Primpolynom) bezeichnet, wenn es sich nicht in Faktoren zerlegen lässt.
Beispiel:

Die möglichen Nullstellen ergeben sich aus den Teilern des konstanten Glieds: 

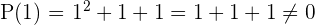
Berechnung von Nullstellen und Polynomfaktoren
Basierend auf den Teilern des konstanten Glieds wenden wir das Resttheorem an, um herauszufinden, für welche Werte die Division lösbar ist.
Beispiel:
Ermittle die Nullstellen der Polynomfunktion 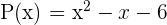 .
.
1 Zuerst werden die Teiler des konstanten Glieds ermittelt. Diese sind 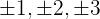 .
.
2 Setze die Teiler in die Funktion ein.
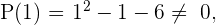


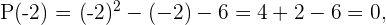
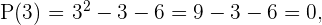
Da ein Polynom zweiten Grades vorliegt, besitzt die Funktion höchstens zwei Nullstellen.
3 Die Nullstellen sind 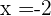 und
und  .
.
4 Die Faktorschreibweise lautet 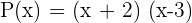
Beispiel:
Ermittle die Nullstellen der Polynomfunktion 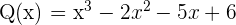
1 Zuerst werden die Teiler des konstanten Glieds ermittelt. Diese sind 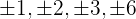 .
.
2 Setze die Teiler in die Funktion ein.

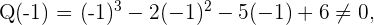

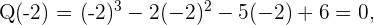
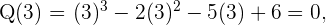
Da ein Polynom dritten Grades vorliegt, besitzt die Funktion höchstens drei Nullstellen.
3 Die Nullstellen sind 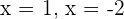 y
y  .
.
4 Die Faktorschreibweise lautet

Beispiel:
Ermittle die Nullstellen der Polynomfunktion 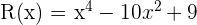
1 Ermittle zuerst die Teiler des konstanten Glieds. Diese sind 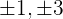 .
.
2 Setze die Teiler in die Funktion ein.

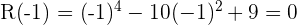
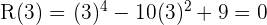
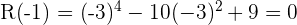
Da ein Polynom vierten Grades vorliegt, besitzt die Funktion höchstens vier Nullstellen.
3 Die Nullstellen sind 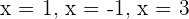 y
y 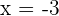 .
.
4 Die Faktorschreibweise lautet 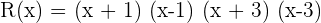
Mit KI zusammenfassen:













