Kapitel
- Entscheide, ob die folgenden mathematischen Ausdrücke Polynome sind oder nicht
- Schreibe in mathematischen Ausdrücken
- Gegeben sind die Polynome P,Q,R,S,T,U:
- Gegeben sind die Polynome P,Q,R:
- Multipliziere folgende Ausdrücke
- Dividiere folgende Ausdrücke
- Dividiere mithilfe des Horner Schemas
- Bestimme den Rest der folgenden Rechenoperationen, ohne die Divisionen durchzuführen
- Zeige, welche Divisionen vollständig aufgehen
- Überprüfe, ob folgende Polynome die angegebenen Faktoren haben
- Berechne die angegebenen Werte
- Berechne die angegebenen Koeffizienten
- Berechne den Wert für k
- Berechne den Wert für m
- Finde das Polynom, das folgende Bedingungen erfüllt
- Berechne den Wert für a
Übungsaufgaben mit Lösungen zu Polynomen mit konstantem Glied unterschiedlichen Grades, geordneten Polynomen, Summe und Differenz von Polynomen, Multiplikation von Polynomen, Division von Polynomen, das Horner Schema, Restsatz, Rest eines Polynoms und Faktorisierung.

Entscheide, ob die folgenden mathematischen Ausdrücke Polynome sind oder nicht
Entscheide, ob die folgenden mathematischen Ausdrücke Polynome sind oder nicht.
Falls ja, gib den Grad des Polynoms und das konstante Glied an.
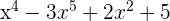
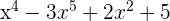
Grad:  , konstantes Glied:
, konstantes Glied:  .
.
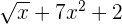
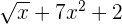
Hierbei handelt es sich nicht um ein Polynom, da die Variable des ersten Monoms in einer Wurzel steht.
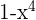
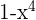
Grad:  , konstantes Glied:
, konstantes Glied:  .
.
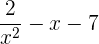
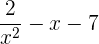
Hierbei handelt es nicht nicht um ein Polynom, da der Exponent  des ersten Monoms keine natürliche Zahl ist.
des ersten Monoms keine natürliche Zahl ist.


Grad:  , konstantes Glied:
, konstantes Glied: .
.


Hierbei handelt es sich nicht um ein Polynom, da der Exponent des zweiten Monoms keine natürliche Zahl ist.
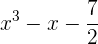
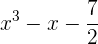
Grad:  , konstantes Glied:
, konstantes Glied: 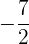 .
.
Schreibe in mathematischen Ausdrücken
Ein geordnetes Polynom ohne konstantes Glied.
Ein geordnetes Polynom ohne konstantes Glied.
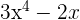
Ein nicht geordnetes und vollständiges Polynom.
Ein nicht geordnetes und vollständiges Polynom.
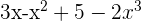
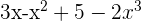
Ein vollständiges Polynom ohne konstantes Glied.
Ein vollständiges Polynom ohne konstantes Glied.
Nicht möglich
Ein Polynom vom Grad  , vollständig und mit ungeraden Koeffizienten.
, vollständig und mit ungeraden Koeffizienten.
Ein Polynom vom Grad  , vollständig und mit ungeraden Koeffizienten.
, vollständig und mit ungeraden Koeffizienten.

Gegeben sind die Polynome P,Q,R,S,T,U:
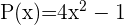
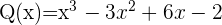
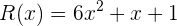
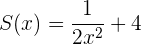
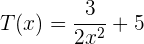
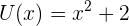
Wir berechnen:


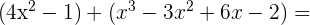
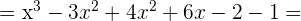
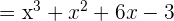


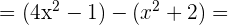




= 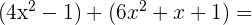
= 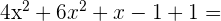
= 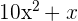
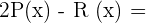
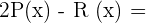
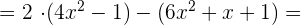


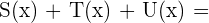
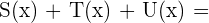
= 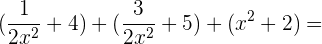
= 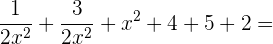
= 
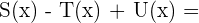
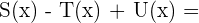
= 
= 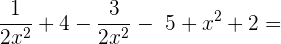
= 
Gegeben sind die Polynome P,Q,R:
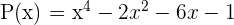


Wir berechnen:
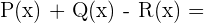
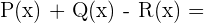

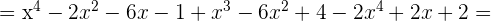


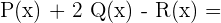
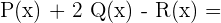
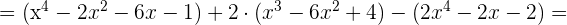

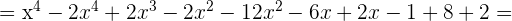
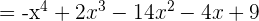

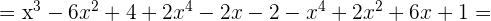
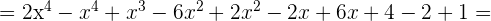
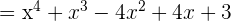
Multipliziere folgende Ausdrücke
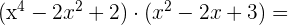
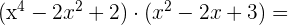
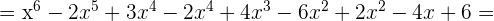
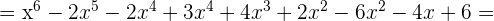
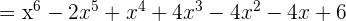
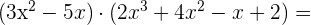
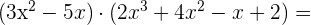
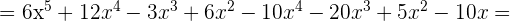
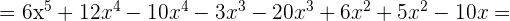

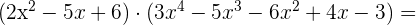
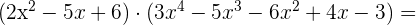
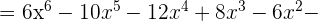
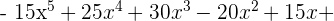
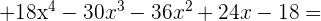

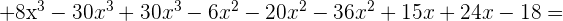
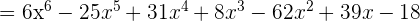
Dividiere folgende Ausdrücke
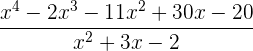
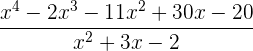
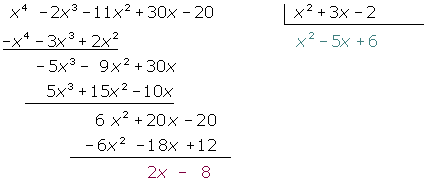
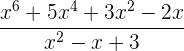
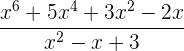
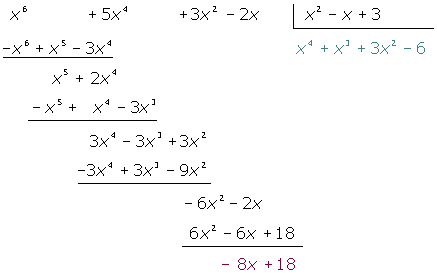
Gegeben sind folgende Polynome:
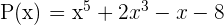

Wir lösen
 :
:
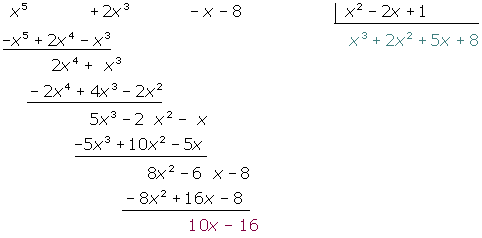
Dividiere mithilfe des Horner Schemas
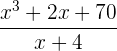
Horner Schema:
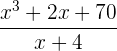
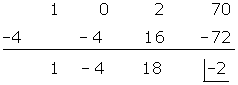
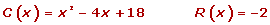

Horner Schema:

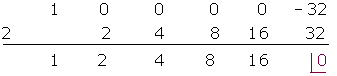
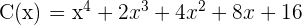
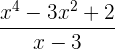
Horner Schema:
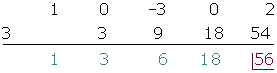
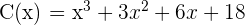
Bestimme den Rest der folgenden Rechenoperationen, ohne die Divisionen durchzuführen
Bestimme bei den folgenden Rechenoperationen, ohne dabei die Divisionen durchzuführen, welcher Rest bleibt:
Um den Rest zu bestimmen, wenden wir den Restsatz an. Dieser besagt, dass der Rest der Division eines Polynoms  durch ein Polynom der Form
durch ein Polynom der Form  der numerische Wert des besagten Polynoms für den Wert von
der numerische Wert des besagten Polynoms für den Wert von  ist
ist
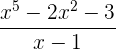
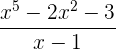
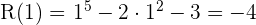
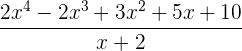
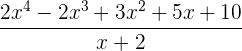
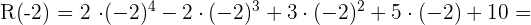
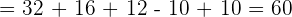
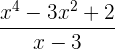
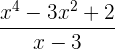

Zeige, welche Divisionen vollständig aufgehen
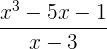
Wir wenden den Restsatz an. Falls der Rest 0 ist, geht die Division exakt auf.
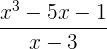

Bei dieser Division bleibt ein Rest.
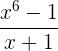
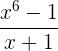
Division geht ohne Rest auf.
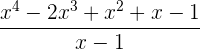
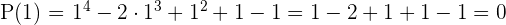
Division geht ohne Rest auf.
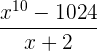
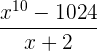
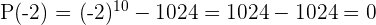
Division geht ohne Rest auf.
Überprüfe, ob folgende Polynome die angegebenen Faktoren haben
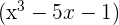 hat als Faktor
hat als Faktor 
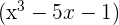 hat als Faktor
hat als Faktor 
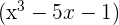 ist teilbar durch
ist teilbar durch  , aber nur dann, wenn gilt
, aber nur dann, wenn gilt  .
.

 ist kein Faktor.
ist kein Faktor.
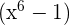 hat als Faktor
hat als Faktor 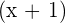
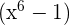 hat als Faktor
hat als Faktor 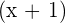
 ist teilbar durch
ist teilbar durch 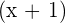 , aber nur dann, wenn gilt
, aber nur dann, wenn gilt  .
.
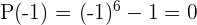
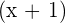 ist kein Faktor.
ist kein Faktor.
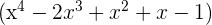 hat als Faktor
hat als Faktor 
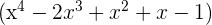 hat als Faktor
hat als Faktor 
 .
.
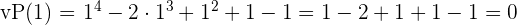
 ist kein Faktor.
ist kein Faktor.
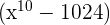 hat als Faktor
hat als Faktor 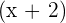
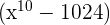 hat als Faktor
hat als Faktor 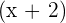
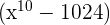 ist teilbar durch
ist teilbar durch 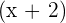 , aber nur dann, wenn gilt
, aber nur dann, wenn gilt  .
.
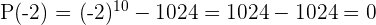
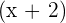 ist ein Faktor.
ist ein Faktor.
Berechne die angegebenen Werte
Bestimme  und
und  , sodass das Polynom
, sodass das Polynom 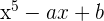 teilbar durch
teilbar durch 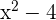 ist.
ist.
Bestimme  und
und  , sodass das Polynom
, sodass das Polynom 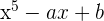 teilbar durch
teilbar durch 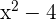 ist.
ist.
Wir zerlegen in Faktoren
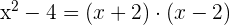
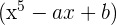 ist teilbar durch
ist teilbar durch  , aber nur dann, wenn gilt
, aber nur dann, wenn gilt  und
und 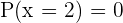
Durch den Restsatz wissen wir, dass der Rest 0 ist
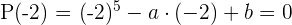
Wir führen aus


Durch den Restsatz wissen wir, dass der Rest 0 ist
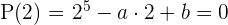
Wir berechnen
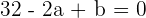

Wir erhalten zwei Gleichungen mit zwei Unbekannten. Wir lösen das Gleichungssystem mithilfe des Additionsverfahrens
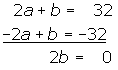

Berechne die angegebenen Koeffizienten
Bestimme die Koeffizienten  und
und  , sodass das Polynom
, sodass das Polynom 
teilbar durch 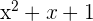 ist.
ist.
Bestimme die Koeffizienten  und
und  , sodass das Polynom
, sodass das Polynom 
teilbar durch 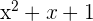 ist.
ist.
Wir dividieren
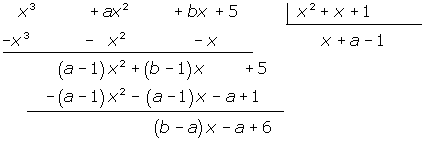
Damit die Division teilbar ist, muss sie vollständig aufgehen. Das heißt,
es darf kein Rest bleiben.
Damit der Rest null ist, muss der Koeffizient von  und der Koeffizient
und der Koeffizient
des konstanten Glieds null sein
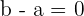
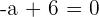


Berechne den Wert für k
Den Wert für  bestimmen, damit beim Dividieren von
bestimmen, damit beim Dividieren von 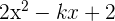 durch
durch 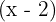 als Rest
als Rest  bleibt.
bleibt.
Den Wert für  finden, damit beim Dividieren von
finden, damit beim Dividieren von 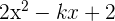 durch
durch 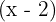 als Rest
als Rest  bleibt.
bleibt.
Wir wenden den Restsatz an und finden heraus, dass Rest  bleibt
bleibt
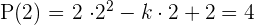
Wir führen durch
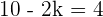
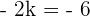

Berechne den Wert für m
Den Wert für m bestimmen, sodass bei 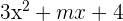
 eine der Nullstellen ist.
eine der Nullstellen ist.
Den Wert für  bestimmen, sodass bei
bestimmen, sodass bei 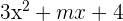
 eine der Nullstellen ist.
eine der Nullstellen ist.
Wenn  eine Nullstelle des Polynoms ist, muss der numerische Wert des Polynoms für diesen Wert null sein
eine Nullstelle des Polynoms ist, muss der numerische Wert des Polynoms für diesen Wert null sein
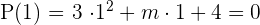
Wir führen aus


Finde das Polynom, das folgende Bedingungen erfüllt
Bestimme ein Polynom vierten Grades, das teilbar durch 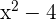 ist
ist
und für  und
und  null wird.
null wird.
Ein Polynom vierten Grades bestimmen, das teilbar durch 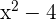 ist
ist
und für  und
und  null wird.
null wird.
Wenn es für  und
und  null wird, sind
null wird, sind  und
und 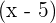 somit Faktoren des
somit Faktoren des
des gesuchten Polynoms
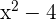 ist ein weiterer Faktor, da das Polynom teilbar durch
ist ein weiterer Faktor, da das Polynom teilbar durch 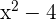 ist
ist
Wir multiplizieren die Faktoren:
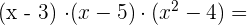
Wir multiplizieren als Erstes die ersten beiden
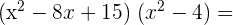
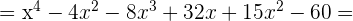
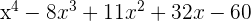
Berechne den Wert für a
Den Wert für a berechnen, sodass das Polynom 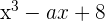 die Nullstelle
die Nullstelle  hat
hat
und die weiteren Nullstellen berechnen.
Den Wert für a berechnen, sodass das Polynom 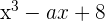 die Nullstelle
die Nullstelle  hat
hat
und die weiteren Nullstellen berechnen
Wir berechnen den Wert für  . Wir wissen, dass der numerischen Wert des Polynoms
. Wir wissen, dass der numerischen Wert des Polynoms
für
 null sein muss
null sein muss
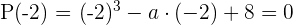

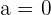
Wir faktorisieren mit dem Horner Schema
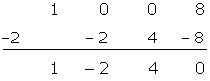

Wir setzen den zweiten Faktor gleich null und lösen die Gleichung zweiten Grades
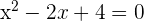
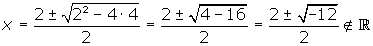
Mit KI zusammenfassen:













