Kapitel

Methoden zur Faktorisierung und Ermittlung von Nullstellen
In einer Gleichung der Form 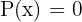 , kann das Polynom
, kann das Polynom  in Faktoren ersten und zweiten Grades zerlegt werden. Dafür wendet man den Divisionssatz und das Horner-Schema an. Außerdem zieht man die allgemeine Formel zur Hilfe heran.
in Faktoren ersten und zweiten Grades zerlegt werden. Dafür wendet man den Divisionssatz und das Horner-Schema an. Außerdem zieht man die allgemeine Formel zur Hilfe heran.
Welcher Zusammenhang besteht zwischen den Nullstellen eines Polynoms und ihrer Faktorisierung?
Bei einem Polynom der Form 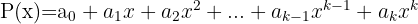 des Grades
des Grades  mit den Nullstellen
mit den Nullstellen 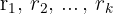 faktorisiert man wie folgt
faktorisiert man wie folgt
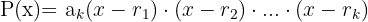
Aufgaben zur Lösung von Gleichungen nach Horner-Schema und Divisionssatz
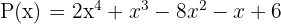
Finde die Teiler des konstanten Glieds: 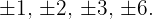
Wende den Divisionssatz an und du erhältst die Werte, für welche die Division exakt ist. Beginne mit

Da das Ergebnis Null ist, ist die Division von  durch
durch 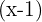 exakt, das heißt man kann nun das Horner-Schema anwenden.
exakt, das heißt man kann nun das Horner-Schema anwenden.
Anwendung des Horner-Schemas.
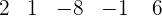
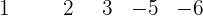

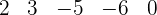
Da die Division exakt ist, ist D = d · c, das heißt
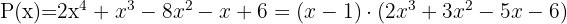
Daraus lässt sich schließen, dass  eine Nullstelle des Polynoms
eine Nullstelle des Polynoms  ist.
ist.
Führe nun dieselben Schritte für den zweiten Faktor durch.
Prüfe erneut mit 1, da der erste Faktor eine Quadratzahl sein könnte. Verwende dafür den Quotienten, der sich aus dem Horner-Schema ergibt 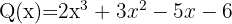
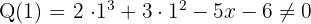
Da das Ergebnis nicht Null ist, prüfe mit einem anderen Teiler, z.B. mit -1
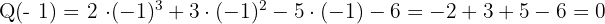
Da das Ergebnis gleich Null ist, berechne die Division von  durch
durch 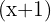 nach dem Horner-Schema.
nach dem Horner-Schema.
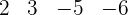
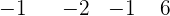

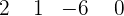
Man kommt zu folgendem Schluss:
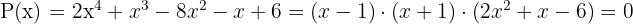
Eine weitere Nullstelle ist  .
.
Da nun nur noch die Nullstellen von 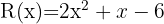 verbleiben und es sich um ein Polynom zweiten Grades handelt, kann die allgemeine Formel angewendet werden. Man könnte auch die vorhergehenden Schritte wiederholen, jedoch hätte diese Vorgehensweise zur Folge, dass nur ganze Nullstellen gefunden werden können und von Nachteil, wenn das Polynom nicht ganze Nullstellen hätte.
verbleiben und es sich um ein Polynom zweiten Grades handelt, kann die allgemeine Formel angewendet werden. Man könnte auch die vorhergehenden Schritte wiederholen, jedoch hätte diese Vorgehensweise zur Folge, dass nur ganze Nullstellen gefunden werden können und von Nachteil, wenn das Polynom nicht ganze Nullstellen hätte.
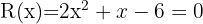
Anhand der allgemeinen Formel ergibt sich
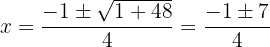
Das heißt
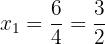
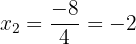
Die Lösungen sind:  ,
,  ,
,  y
y 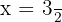
Daraus lässt sich schlussfolgern, dass das Polynom  wie folgt faktorisiert wird
wie folgt faktorisiert wird
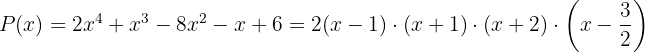

Finde die Teiler des konstanten Glieds: 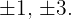
Wende den Divisionssatz an und du erhältst die Werte, für welche die Division exakt ist. Beginne mit 1.
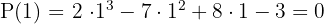
Da das Ergebnis Null ist, ist die Division von  durch
durch 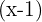 exakt, das heißt man kann nun das Horner-Schema anwenden.
exakt, das heißt man kann nun das Horner-Schema anwenden.

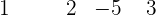


Folglich ist

Daraus lässt sich schließen, dass  eine Nullstelle des Polynoms
eine Nullstelle des Polynoms  ist.
ist.
Führe nun dieselben Schritte für den zweiten Faktor durch.
Prüfe erneut mit 1, da sich diese Nullstelle wiederholen könnte, das heißt, der erste Faktor könnte eine Quadratzahl sein. Verwende dafür den Quotienten, der sich aus dem Horner-Schema ergibt 
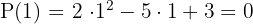
Da das Ergebnis gleich Null ist, berechne die Division von  durch
durch 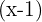 nach dem Horner-Schema.
nach dem Horner-Schema.
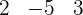
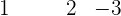

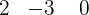

Die Lösungen sind folglich:  y
y 
Daraus lässt sich schlussfolgern, dass das Polynom  wie folgt faktorisiert wird
wie folgt faktorisiert wird
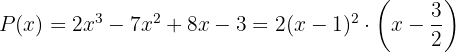
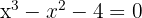
Finde die Teiler des konstanten Glieds: 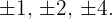
Wende den Divisionssatz an und du erhältst die Werte, für welche die Division exakt ist
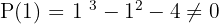

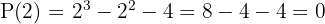
Da das Ergebnis gleich Null ist, ist die Division von  durch
durch 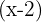 exakt, das heißt man kann nun das Horner-Schema anwenden.
exakt, das heißt man kann nun das Horner-Schema anwenden.

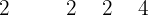


Folglich ist

Da nun nur noch die Nullstellen von  ermittelt werden müssen und es sich hier um eine Gleichung zweiten Grades handelt, verwendet man die allgemeine Formel
ermittelt werden müssen und es sich hier um eine Gleichung zweiten Grades handelt, verwendet man die allgemeine Formel

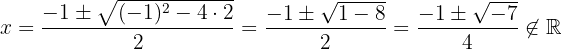
Da sich keine reelle Zahl ergibt, kann das Polynom zweiten Grades nicht weiter zerlegt werden, das heißt, das Polynom wird wie folgt faktorisiert
wird wie folgt faktorisiert
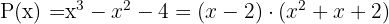
und besitzt als einzige Nullstelle: 

Finde die Teiler des konstanten Glieds:  Wende den Divisionssatz an und du erhältst die Werte, für welche die Division exakt ist.
Wende den Divisionssatz an und du erhältst die Werte, für welche die Division exakt ist.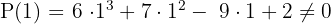
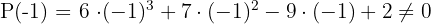
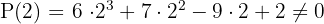

Da das Ergebnis im letzten Fall Null ist, ist die Division von  durch
durch  exakt, das heißt man kann nun das Horner-Schema anwenden.
exakt, das heißt man kann nun das Horner-Schema anwenden.
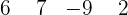
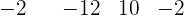


Folglich ist
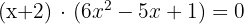
Da nun nur noch die Nullstellen von 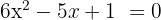 ermittelt werden müssen und es sich hier um eine Gleichung zweiten Grades handelt, verwendet man die allgemeine Formel
ermittelt werden müssen und es sich hier um eine Gleichung zweiten Grades handelt, verwendet man die allgemeine Formel
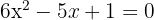
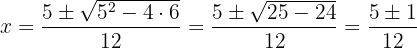
Folglich ist

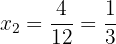
Las soluciones son: 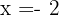 ,
,  y
y 
Daraus lässt sich schlussfolgern, dass das Polynom  wie folgt faktorisiert wird
wie folgt faktorisiert wird
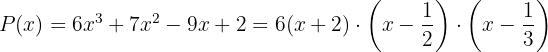
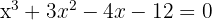
Finde die Teiler des konstanten Glieds:  Wende den Divisionssatz an und du erhältst die Werte, für welche die Division exakt ist.
Wende den Divisionssatz an und du erhältst die Werte, für welche die Division exakt ist.
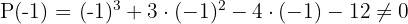

Da das Ergebnis gleich Null ist, ist die Division von  durch
durch 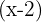 exakt, das heißt, man kann nun das Horner-Schema anwenden.
exakt, das heißt, man kann nun das Horner-Schema anwenden.
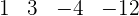



Folglich ist
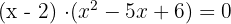
Da nun nur noch die Nullstellen des zweiten Faktors ermittelt werden müssen 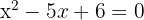 und dieser ein Polynom zweiten Grades ist, kann die allgemeine Formel angewendet werden
und dieser ein Polynom zweiten Grades ist, kann die allgemeine Formel angewendet werden
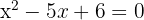

Folglich ist


Die Lösungen sind:  ,
,  ,
, 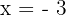 .
.
Daraus lässt sich schlussfolgern, dass das Polynom  wie folgt faktorisiert wird
wie folgt faktorisiert wird

Mit KI zusammenfassen:













