Kapitel
Im Folgenden lösen wir Aufgaben zu den Thematiken:
- Faktorisierung eines Binoms
- Faktorisierung eines perfekten quadratischen Trinoms
- Faktorisierung eines quadratischen Trinoms
- Faktorisierung eines Trinoms zweiten Grades
- Faktorisierung eines Polynoms vierten Grades
- Faktorisierung eines unvollständigen Polynoms dritten Grades
- Faktorisierung durch Anpassung des Gleichungsgrads

Polynomfaktorisierung und Ermittlung von Nullstellen: Aufgaben
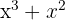
span class="sa">1 Um 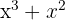 zu faktorisieren, beachte, dass
zu faktorisieren, beachte, dass  ein gemeinsamer Faktor beider Terme ist
ein gemeinsamer Faktor beider Terme ist
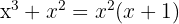
span class="sa">2 Um die Wurzel (=Nullstelle) herauszufinden, muss der Wert von  so gewählt sein, dass die Gleichung Null ergibt. Für
so gewählt sein, dass die Gleichung Null ergibt. Für 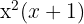 trifft dies in zwei Fällen zu: wenn
trifft dies in zwei Fällen zu: wenn  ist und wenn
ist und wenn  ist
ist
Folglich sind die Wurzeln  und
und 
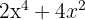
span class="sa">1 Um 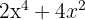 zu faktorisieren, beachte, dass
zu faktorisieren, beachte, dass 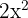 ein gemeinsamer Faktor beider Terme ist
ein gemeinsamer Faktor beider Terme ist
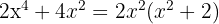
span class="sa">2 In diesem Fall ist  die einzige Nullstelle, da das Polynom
die einzige Nullstelle, da das Polynom  keine Wurzeln hat, d.h. es gibt keine reelle Zahl
keine Wurzeln hat, d.h. es gibt keine reelle Zahl  für die
für die 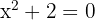 wäre
wäre

span class="sa">1 Wende die Quadratdifferenz an
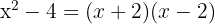
span class="sa">2 Die Wurzeln, mit denen jeder Faktor Null ergibt, sind
 und
und 
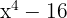
span class="sa">1 Wende die Quadratdifferenz an

span class="sa">2 Wende die Quadratdifferenz erneut beim zweiten Faktor an

span class="sa">3 Die Wurzeln, mit denen jeder Faktor Null ergibt, sind
 y
y 
Beachte, dass der Faktor  keine reelle Wurzel besitzt
keine reelle Wurzel besitzt
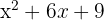
span class="sa">1 Hier liegt ein perfektes quadratisches Trinom vor, das auch als quadratisches Binom geschrieben werden kann. Stelle die folgenden Fragen:
Welche Zahl zum Quadrat ergibt  ? Und welche Zahl zum Quadrat ergibt
? Und welche Zahl zum Quadrat ergibt  ?
?
Prüfe, wann das doppelte Lösungsprodukt gleich  ist
ist
span class="sa">2 Dies ist für  und
und  der Fall, d.h. die Faktorisierung muss wie folgt aussehen
der Fall, d.h. die Faktorisierung muss wie folgt aussehen

span class="sa">3 Die Wurzel, mit denen jeder Faktor Null ergibt, ist
 . Man nennt sie auch doppelte Nullstelle
. Man nennt sie auch doppelte Nullstelle

span class="sa">1 Wende in diesem Fall die allgemeine Formel für Gleichungen zweiten Gradesan. Dafür muss die Gleichung gleich Null gesetzt werden, das heißt  . Ermittle die Werte von
. Ermittle die Werte von  (Nullstellen der Gleichung) mithilfe der allgemeinen Formel
(Nullstellen der Gleichung) mithilfe der allgemeinen Formel
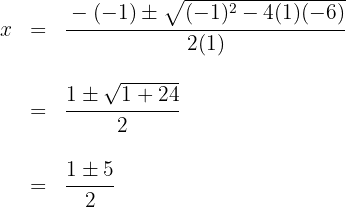
Löse auf und du erhältst die Nullstellen 
span class="sa">2 In diesem Fall sind die Faktoren der Gleichung
 .
.

span class="sa">1 Setze das Polynom gleich Null und führe einen Variablentausch durch 
Durch Einsetzen der neuen Variable erhältst du 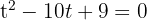
span class="sa">2 Löse die Gleichung zweiten Grades auf
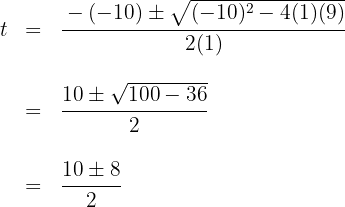
Du erhältst die Nullstellen 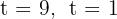
span class="sa">3 Durch Variablentausch erhältst du  ; löse auf und du erhältst die Nullstellen
; löse auf und du erhältst die Nullstellen

span class="sa">4 In diesem Fall sind die Faktoren der Gleichung
 .
.
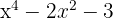
span class="sa">1 Setze das Polynom gleich Null und führe einen Variablentausch durch 
Durch Einsetzen der neuen Variable erhältst du 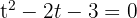
span class="sa">2 Löse die Gleichung zweiten Grades auf

Du erhältst die Nullstellen 
span class="sa">3 Durch Variablentausch erhältst du  ; löse auf und du erhältst die Nullstellen
; löse auf und du erhältst die Nullstellen
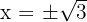 ; beachte, dass
; beachte, dass 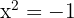 keine Lösungen besitzt
keine Lösungen besitzt
span class="sa">4 In diesem Fall sind die Faktoren der Gleichung
 .
.
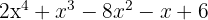
span class="sa">1 Finde die Teiler des konstanten Glieds. Diese sind  .
.
span class="sa">2 Durch Anwendung des Divisionssatzes kannst du ermitteln für welche Werte die Division exakt ist.

span class="sa">3 Führe eine Division nach dem Horner-Schema durch
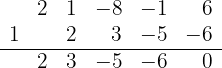
Da die Division exakt ist, ist  eine Nullstelle und das entsprechende Polynom ist
eine Nullstelle und das entsprechende Polynom ist

span class="sa">4 Wende die gleiche Vorgehensweise beim zweiten Faktor an. Prüfe mit  , da der erste Faktor eine Quadratzahl sein könnte.
, da der erste Faktor eine Quadratzahl sein könnte.

 ist also keine Nullstelle des zweiten Faktors. Prüfe mit
ist also keine Nullstelle des zweiten Faktors. Prüfe mit 
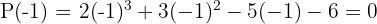
span class="sa">5 Führe eine Division nach dem Horner-Schema durch
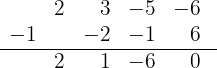
Da die Division exakt ist, ist  eine Nullstelle und das entsprechende Polynom ist
eine Nullstelle und das entsprechende Polynom ist
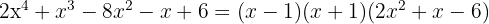
span class="sa">6 Ermittle nun mithilfe der Gleichung zweiten Grades den dritten Faktor oder auf die gleiche Weise wie gerade, wobei dann der Nachteil ist, dass man nur ganze Nullstellen finden kann.
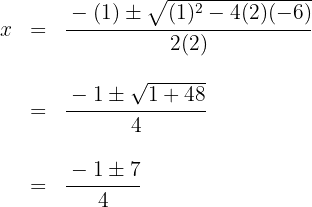
Die Nullstellen sind 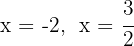 und das entsprechende Polynom ist
und das entsprechende Polynom ist
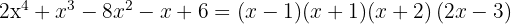

span class="sa">1 Finde die Teiler des konstanten Glieds. Diese sind 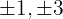 .
.
span class="sa">2 Durch Anwendung des Divisionssatzes kannst du ermitteln für welche Werte die Division exakt ist.
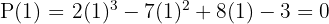
span class="sa">3 Führe eine Division nach dem Horner-Schema durch
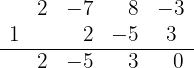
Da die Division exakt ist, ist  eine Nullstelle und das entsprechende Polynom ist
eine Nullstelle und das entsprechende Polynom ist

span class="sa">4 Wende die gleiche Vorgehensweise beim zweiten Faktor an. Prüfe mit  , da der erste Faktor eine Quadratzahl sein könnte.
, da der erste Faktor eine Quadratzahl sein könnte.

span class="sa">5 Führe eine Division nach dem Horner-Schema durch

Da die Division exakt ist, ist  ine Nullstelle und das entsprechende Polynom ist
ine Nullstelle und das entsprechende Polynom ist
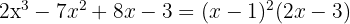
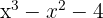
span class="sa">1 Finde die Teiler des konstanten Glieds. Diese sind 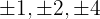 .
.
span class="sa">2 Durch Anwendung des Divisionssatzes kannst du ermitteln für welche Werte die Division exakt ist.
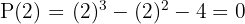
span class="sa">3 Führe eine Division nach dem Horner-Schema durch
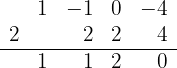
Da die Division exakt ist, ist  eine Nullstelle und das entsprechende Polynom ist
eine Nullstelle und das entsprechende Polynom ist
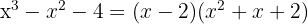
span class="sa">4 Ermittle nun mithilfe der Gleichung zweiten Grades den zweiten Faktor oder auf die gleiche Weise wie gerade, wobei dann der Nachteil ist, dass man nur ganze Nullstellen finden kann.
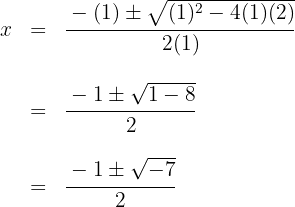
Da die Diskriminante negativ ist, besitzt das Polynom keine reellen Nullstellen. Daher ist die einzige Nullstelle  und das entsprechende Polynom ist
und das entsprechende Polynom ist
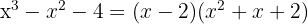
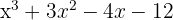
span class="sa">1 Finde die Teiler des konstanten Glieds. Diese sind 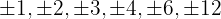 .
.
span class="sa">2 Durch Anwendung des Divisionssatzes kannst du ermitteln für welche Werte die Division exakt ist.

span class="sa">3 Führe eine Division nach dem Horner-Schema durch
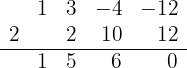
Da die Division exakt ist, ist  eine Nullstelle und das entsprechende Polynom ist
eine Nullstelle und das entsprechende Polynom ist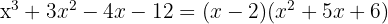
span class="sa">4 Ermittle nun mithilfe der Gleichung zweiten Grades den zweiten Faktor oder auf die gleiche Weise wie gerade, wobei dann der Nachteil ist, dass man nur ganze Nullstellen finden kann.
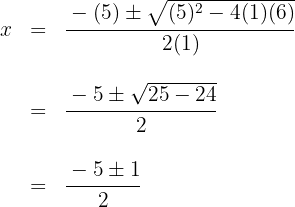
Die Nullstellen des zweiten Faktors sind 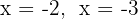 und das entsprechende Polynom ist
und das entsprechende Polynom ist
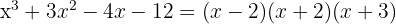
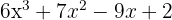
span class="sa">1 Finde die Teiler des konstanten Glieds. Diese sind  .
.
span class="sa">2 Durch Anwendung des Divisionssatzes kannst du ermitteln für welche Werte die Division exakt ist.
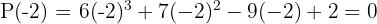
span class="sa">3 Führe eine Division nach dem Horner-Schema durch

Da die Division exakt ist, ist  eine Nullstelle und das entsprechende Polynom ist
eine Nullstelle und das entsprechende Polynom ist

span class="sa">4 Ermittle nun mithilfe der Gleichung zweiten Grades den zweiten Faktor oder auf die gleiche Weise wie gerade, wobei dann der Nachteil ist, dass man nur ganze Nullstellen finden kann.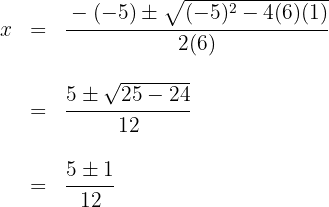
Die Nullstellen des zweiten Faktors sind  und das entsprechende Polynom ist
und das entsprechende Polynom ist

Polynomfaktorisierung: Aufgaben


Klammere den gemeinsamen Faktor  aus
aus
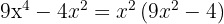
Schreibe die quadratische Differenz als Summe mal Differenz aus
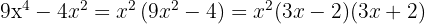
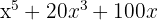
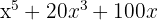
Klammere den gemeinsamen Faktor  aus
aus

Du erhältst ein perfektes quadratisches Trinom, das man auch als Binom zum Quadrat darstellen kann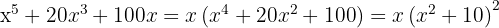
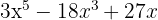
Klammere den gemeinsamen Faktor  aus
aus
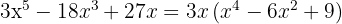
Du erhältst ein perfektes quadratisches Trinom, das man auch als Binom zum Quadrat darstellen kann

Schreibe die quadratische Differenz als Summe mal Differenz aus
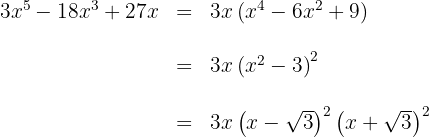
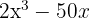
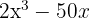
Klammere den gemeinsamen Faktor  aus
aus
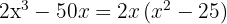
Schreibe die quadratische Differenz als Summe mal Differenz aus

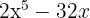
Klammere den gemeinsamen Faktor  aus
aus

Schreibe die quadratische Differenz als Summe mal Differenz aus
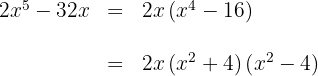
Der zweite Faktor ist ein irreduzibles Polynom oder Primpolynom
Der dritte Faktor ist eine Quadratdifferenz, die als Summe mal Differenz dargestellt wird
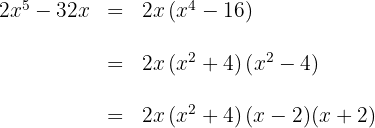
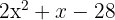
Setze das Trinom zweiten Grades gleich Null und löse die Gleichung auf

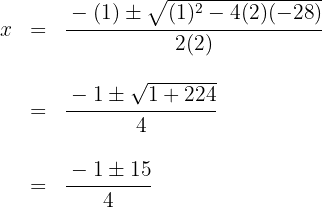
Die Nullstellen sind 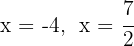 und das entsprechende Polynom ist
und das entsprechende Polynom ist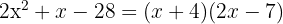
Linearfaktorzerlegung: Aufgaben

Bei dieser Aufgabe kann zweimal ein gemeinsamer Faktor ausgeklammert werden. Klammere bei den ersten beiden Summanden  aus und bei den zweiten beiden
aus und bei den zweiten beiden 

Klammere den gemeinsamen Faktor 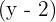 aus
aus



ist eine quadratische Differenz
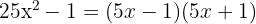
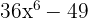
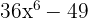
Schreibe die quadratische Differenz als Summe mal Differenz aus
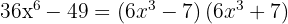

Du erhältst ein perfektes quadratisches Trinom, das man auch als Binom zum Quadrat darstellen kann
Das Quadrat von  ist
ist  , das Quadrat von
, das Quadrat von  ist
ist  und das Doppelte von
und das Doppelte von  mal
mal  ist
ist 

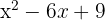
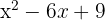
Du erhältst ein perfektes quadratisches Trinom, das man auch als Binom zum Quadrat darstellen kann
Das Quadrat von  ist
ist  , das Quadrat von
, das Quadrat von  ist
ist  und das Doppelte von
und das Doppelte von  mal
mal  ist
ist 
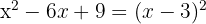

Du erhältst ein perfektes quadratisches Trinom, das man auch als Binom zum Quadrat darstellen kann
Das Quadrat von  ist
ist  , das Quadrat von
, das Quadrat von  ist
ist  und das Doppelte von
und das Doppelte von  mal
mal  ist
ist 
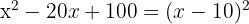


Du erhältst ein perfektes quadratisches Trinom, das man auch als Binom zum Quadrat darstellen kann
Das Quadrat von  ist
ist  , das Quadrat von
, das Quadrat von  ist
ist  und das Doppelte von
und das Doppelte von  mal
mal  ist
ist 

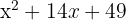
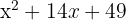
Du erhältst ein perfektes quadratisches Trinom, das man auch als Binom zum Quadrat darstellen kann
Das Quadrat von  ist
ist  , das Quadrat von
, das Quadrat von  ist
ist  und das Doppelte von
und das Doppelte von  mal
mal  ist
ist 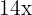
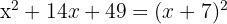
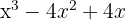
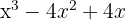
Klammere den gemeinsamen Faktor aus

Du erhältst ein weiteres perfektes quadratisches Trinom
Das Quadrat von  ist
ist  , das Quadrat von
, das Quadrat von  ist
ist  und das Doppelte von
und das Doppelte von  mal
mal  ist
ist 
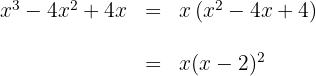


Klammere den gemeinsamen Faktor aus
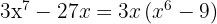
Schreibe die quadratische Differenz als Summe mal Differenz aus

Wende die Würfelsumme und -differenz an
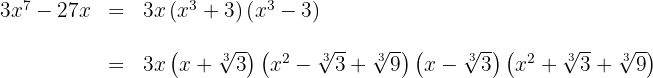
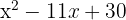
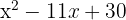
Setze das Polynom gleich Null
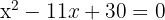
Löse die Gleichung zweiten Grades auf
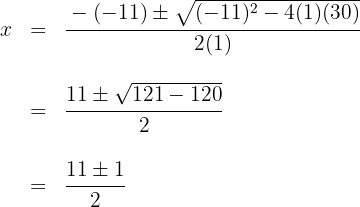
Die Nullstellen sind 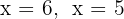 und das entsprechende Polynom ist
und das entsprechende Polynom ist



Löse die Gleichung zweiten Grades auf

Die Nullstellen sind 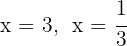 und das entsprechende Polynom ist
und das entsprechende Polynom ist
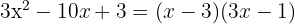
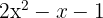
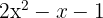
Löse die Gleichung zweiten Grades auf
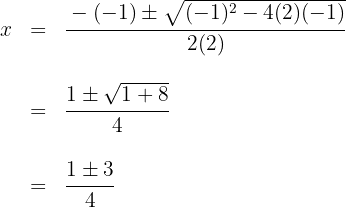
Die Nullstellen sind 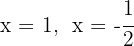 und das entsprechende Polynom ist
und das entsprechende Polynom ist

Mit KI zusammenfassen:













