Kapitel
Was besagt der Satz?
Wie wir wissen, erhalten wir bei der Division eines Polynoms 
durch 
einen Quotienten 
und einen Rest 
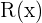
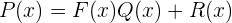
wobei der Grad von 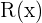niedriger als der Grad von sein muss. Die Division kann auch wie folgt dargestellt werden:
Der Polynomrestsatz hilft uns dabei, den Rest 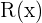zu bestimmen, der bleibt, wenn man durch ein Polynom der Form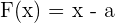 
teilt. Der Satz besagt Folgendes:
Satz: Gegeben ist ein Polynom . Somit entspricht der Rest, der bei der Division von durch 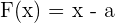bleibt, dem Ergebnis, das man erhält, wenn man das Polynom von 
berechnet. Das heißt:
Beispiel: Gegeben sind die Polynome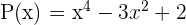 
und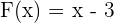 
. Wir setzen ein
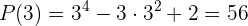
Deshalb muss der Rest, der bei der Division von durch bleibt, 56 sein. Um dies zu überprüfen, wenden wir das Horner-Schema an. Wir schreiben alle Koeffizienten des Polynoms in die erste Zeile unserer Übersicht und stellen die 3 etwas weiter nach links:
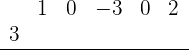
Danach schreiben wir die 1 (der erste Koeffizient von ) unter die horizontale Linie:
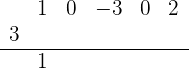
Wir multiplizieren die 1 unter der Linie mit 3 (das Ergebnis ist 3) und schreiben das Ergebnis unter den nächsten Koeffizienten von :
Dann subtrahieren wir die Zahlen, die in der Spalte des zweiten Koeffizienten (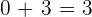
) stehen und notieren das Ergebnis unterhalb der Linie:
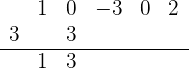
Wir wiederholen die vorhergehenden Schritte. Wir multiplizieren die Zahl, die unterhalb der Linie steht mit 3 (das Ergebnis ist 9) und schreiben das Ergebnis unter den zweiten Koeffizienten von . Schließlich addieren wir die Zahlen:
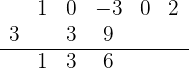
Wir wiederholen die Schritte, dieses Mal mit der Zahl 6:
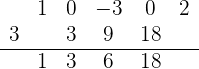
Wir wiederholen die Schritte noch einmal, dieses Mal mit der Zahl 18:
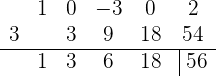
Nun sehen wir, dass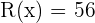 
und somit unser gewünschtes Ergebnis ist.
Bemerkung: Wie wir am vorhergehenden Beispiel sehen, ermittlen wir mit dem Restsatz nur den Rest, der bei der Division eines Polynoms bleibt. Wenn wir den Quotienten herausfinden möchten, müssen wir die vollständige Division durchführen.
Bemerkung: Der Satz besagt, dass wir durch ein Polynom der Form 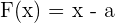dividieren. Wenn wir ein Polynom der Form 
haben, schreiben wir
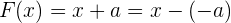
Um also den Rest herauszufinden, werten wir einfach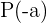 
aus. Mit anderen Worten, wir nehmen das konstante Glied von , aber mit umgedrehtem Vorzeichen.
Bemerkung: Dieser Satz ist sehr wichtig, doch er besagt uns nicht, ob ein Polynom ein Faktor von ist. Wir wissen, dass 
ein Faktor von ist, wenn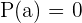 
. Dieser Satz ist bekannt als Faktorsatz.
Übungsaufgaben
Berechne mit dem Restsatz den Rest der Division von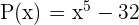 
geteilt durch 
. Überprüfe später mithilfe des Horner-Schemas.
1 Wir wenden zunächst den Restsatz an. Wir werten das Polynomy für 
aus:
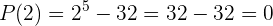
Da der Rest 0 ist, stellen wir fest, dass ein Faktor von ist.
1 Nun überprüfen wir mithilfe des Horner-Schemas. Zuerst schreiben wir die Koeffizienten des Polynoms in die erste Zeile (wir denken daran, alle Koeffizienten aufzuschreiben, auch die der Terme 
, 
usw.); danach schreiben wir die 2 leicht nach links versetzt und ziehen den ersten Koeffizienten des Polynoms nach unten:
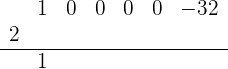
Wir multiplizieren die Zahl, die unter der horizontalen Linie steht, mit 2 und schreiben sie unter den Koeffizienten des zweiten Terms. Danach addieren wir die Terme dieser Spalte:
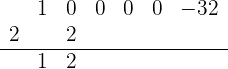
Wir wiederholen den Vorgang für die folgende Zahl, die unterhalb der horizontalen Linie steht:
Wir wiederholen:
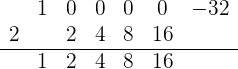
und erhalten schließlich:
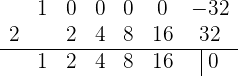
Wir sehen wir nun, dass der Rest der Division 0 ist.
Gegeben ist das Polynom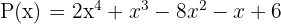 
. Bestimme den Rest, der bei der Division bleibt. Geteilt durch:
a 
b 
c 
d
Wir wenden bei allen Fällen den Restsatz an:
a
Um den Rest zu bestimmen, reicht es, für 
zu berechnen. Nämlich
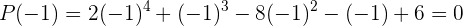
Somit ist der Rest 0.
b
In diesem Fall berechnen wir für 
wie folgt:
Somit ist der Rest hier auch 0.
c
Nun berechnen wir für 
. Das heißt,
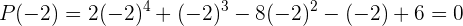
Deshalb ist der Rest 0.
d
Schließlich berechnen wir für , um den Rest zu bestimmen. Somit gilt
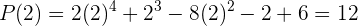
Hier ist der Rest 12.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
