Finde heraus, bei welchen der folgenden Terme es sich um Monome handelt. Gib auch den Grad und Koeffizienten des jeweiligen Monoms an.
a 
b 
c 
d 
e 
f 
g 
Zur Erinnerung: Monome sind immer ein Produkt und eine Potenz mit einer natürlichen Zahl als Exponent. Die Koeffizienten können sich aus jeder beliebigen Rechenoperation zusammensetzen.
a
Es handelt sich um ein Monom mit Koeffizient 3 und Grad 3.
b
Hier liegt kein Monom vor, da 
eine negative Potenz hat (keine natürliche Zahl).
c
Hier liegt kein Monom vor, da der Term eine Summe enthält.
d
Es handelt sich um ein Monom: die Wurzel kann im Koeffizient erscheinen. Der Koeffizient des Monoms ist 
und der Grad 1.
e
Auch hier liegt ein Monom vor, obwohl eine Division vorliegt, da diese den Koeffizienten betrifft. Der Koeffizient ist 
und der Grad 4.
f
Hier liegt kein Monom vor, da ein Bruch vorliegt, der sich auf die Variable bezieht.
g
Hier liegt kein Monom vor, da die Variable mit der Wurzel zusammenhängt. Ebenso könnte man damit argumentieren, dass die Variable die Division (1/2) in der Potenz enthält, also keine natürliche Zahl.
Finde heraus, ob es sich bei den folgenden Termen um Polynome handelt. Wenn ja, gib den Grad und das konstante Glied des Polynoms an.
a 
b 
c 
d 
e 
f 
g 
Zur Erinnerung: ein Polynom ist eine Summe aus Monomen. Der Grad des Polynoms ist der des Monoms der höchsten Ordnung.
a
Hier liegt ein Polynom fünften Grades vor. Das konstante Glied ist ebenso 5.
b
Hier liegt kein Polynom vor, da eine Quadratwurzel im Term enthalten ist.
c
Hier liegt ein Polynom vierten Grades vor. Das konstante Glied ist 1.
d
Das ist kein Polynom, da der Term 
einen negativen Exponenten enthält.
e
Hier liegt ein Polynom fünften Grades vor. Das konstante Glied ist 0.
f
Das ist kein Polynom, da der Term 
einen negativen Exponenten enthält.
g
Hier liegt ein Polynom dritten Grades vor. Das konstante Glied ist 
Schreibe:
a Ein geordnetes Polynom ohne konstantes Glied.
b Ein vollständiges ungeordnetes Polynom.
c Ein vollständiges Polynom ohne konstantes Glied.
d Ein vollständiges Polynom vierten Grades mit ungleichen Koeffizienten.
Dies ist eine offene Aufgabe, das heißt, es gibt viele richtige Lösungen. Hier führen wir einige mögliche Lösungen auf.
a Ein geordnetes Polynom ohne konstantes Glied.
Jedes der folgenden Polynome ist korrekt:
b Ein vollständiges ungeordnetes Polynom.
Jedes der folgenden Polynome ist korrekt:
c Ein vollständiges Polynom ohne konstantes Glied.
Ein solches Polynom existiert nicht. Damit ein Polynom vollständig ist, muss es ein konstantes Glied enthalten.
d Ein vollständiges Polynom vierten Grades mit ungleichen Koeffizienten.
Jedes der folgenden Polynome ist korrekt:
Berechnung von Polynomen
Finde den numerischen Wert des Polynoms 
für die Werte
a 
b 
c 
Um das Polynom zu lösen, setzt man die jeweiligen Werte von in 
ein:
a
Der Wert ist:
b
Ermittle jetzt das Ergebnis für -1:
c
Ermittle als letztes das Ergebnis für 2
Löse die folgenden Rechenaufgaben mit Monomen:
a 
b 
c 
d 
e 
f 
g 
h 
i 
j 
k 
a
Zur Erinnerung: beim Addieren von Monomen werden die Koeffizienten addiert, deren Variablen denselben Exponenten haben:
b
Dieser Fall ist so ähnlich wie der vorherige:
c
Beim Multiplizieren von Monomen werden die Koeffizienten miteinander multipliziert und die Potenzen addiert:
d
Beachte, dass bei dieser Multiplikation von Monomen nur die Potenzen miteinander multipliziert werden, die gleich sind.:
e
Im Gegensatz zur Multiplikation werden bei der Division die Koeffizienten geteilt und die Exponenten voneinander abgezogen:
f
Hier liegt eine Division mit mehreren Variablen vor:
g
Bei Potenzfunktionen werden die Koeffizienten mit der jeweiligen Hochzahl berechnet und die Potenzen der Variablen mit den jeweiligen Potenzen außerhalb der Klammer multipliziert:
h
Löse die Potenzfunktion auf:
i
Löse die Summe aus Monomen:
j
Löse den Bruch:
k
Bei dieser Aufgabe werden unterschiedliche Lösungswege in Kombination benötigt. Wir bemerken, dass die Monome des Nenners nicht addiert werden können, da sie nicht denselben Grad aufweisen. Wir können jeden von ihnen dennoch durch den gemeinsamen Nenner teilen
Gegeben seien die Polynome
Bestimme
a 
b 
c 
d 
e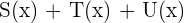 
f 
Hier soll die Summe der Polynome berechnet werden. Zur Erinnerung: die Summe wird gebildet, indem die Koeffizienten der Monome mit dem jeweils selben Grad addiert werden.
a
Man erhält
b
Der Lösungsweg ist
c
Man erhält
d
In diesem Fall müssen zuerst die Koeffizienten von 
mit 2 multipliziert werden:
e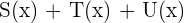
Der Lösungsweg entspricht dem der vorherigen Aufgabe, mit der Besonderheit, dass
f
Berechne die folgenden Polynomprodukte:
a 
b
c 
Finde heraus, um welche Art von binomischen Produkten es sich im Folgenden handelt:
a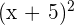 
b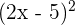 
c 
d 
Es handelt sich um Binome zum Quadrat und konjugierte Binome. Daher kann einfach die binomische Formel angewandt werden.
a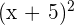
Zur Erinnerung: ein Binom zum Quadrat wird mit der 1. binomischen Formel berechnet
Die Rechenaufgabe löst man also wie folgt:
b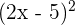
Wie im vorherigen Beispiel handelt es sich hier um ein konjugiertes Binom
c
Hier liegen konjugierte Binome vor, welche anhand der 3. binomischen Formel gelöst werden können:
Löse daher die Aufgabe wie folgt:
d
Dies sind erneut konjugierte Binome, das heißt, man löst sie wie folgt:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
