Übungsaufgaben zu Bruchtermen

Wir klammern den gemeinsamen Faktor jeweils im Nenner und Zähler aus und erhalten somit

Nun kürzen wir den gemeinsamen Faktor und erhalten folgende Vereinfachung

Wir klammern den gemeinsamen Faktor im Zähler aus

Wir multiplizieren den Zähler und den Nenner mit und erhalten so einen äquivalenten Bruchterm

Wir lösen die Klammer im Nenner auf und erhalten

Wir kürzen den gemeinsamen Faktor im Nenner und im Zähler und erhalten

Wir wenden folgendes Schema an:

Wir dividieren Zähler und Nenner nach dem Horner Schema

Bei der Division bleibt kein Rest, deshalb gilt und wir erhalten

Wir vereinfachen den Bruchterm, indem wir den gemeinsamen Faktor des Zählers und des Nenners kürzen

Wir stellen fest, dass der Nenner ist, allerdings befindet sich keiner der Faktoren im Zähler. Deshalb können wir nicht weiter kürzen oder vereinfachen. Aber wir können den Ausdruck wie folgt schreiben

beide Ausdrücke sind korrekt und gültig.

Wir wenden die abc-Formel an und erhalten so die Nullstellen des Polynoms des Zählers und des Polynoms des Nenners. Dies hilft uns, die Polynome als Produkt von Binomen auszudrücken, die durch ihre Nullstellen definiert sind

Wir faktorisieren:

Wir vereinfachen

Wir wenden die abc-Formel an und erhalten so die Nullstellen des Polynoms des Zählers und des Polynoms des Nenners. Dies hilft uns, die Polynome als Produkt von Binomen auszudrücken, die durch ihre Nullstellen definiert sind

Wir faktorisieren:

Wir vereinfachen

Im Zähler wenden wir den Restsatz und das Horner Schema an, um die Nullstellen zu bestimmen

Die Divisoren von sind: {}

Wir dividieren nach dem Horner Schema

Der Zähler entspricht

Das Trinom können wir weiter faktorisieren oder aber die abc-Formel anwenden

Im Nenner klammern wir den gemeinsamen Faktor aus

Um das Trinom zu faktorisieren, wenden wir die abc-Formel an

Addiere die Bruchterme:

Nun müssen wir den gemeinsamen Nenner finden. Dazu müssen wir das kgV der Nenner bestimmen. Wir erhalten

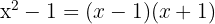
Deshalb gilt

Wir teilen den gemeinsamen Nenner durch die Nenner der Bruchterme und das Ergebnis multiplizieren wir mit dem entsprechenden Zähler

Wir klammern den gemeinsamen Faktor aus

Wir vereinfachen

Subtraktion von Bruchtermen:

Wir müssen die Bruchterme auf einen gemeinsamen Nenner bringen. Dazu müssen wir das kgV der Nenner bestimmen. Wir stellen fest, dass

Deshalb gilt

Wir dividieren den gemeinsamen Nenner durch die Nenner der Bruchterme und das Ergebnis multiplizieren wir mit dem entsprechenden Zähler.

Außerdem müssen wir umformen und erhalten somit

Wir vereinfachen

Das Produkt der zwei Bruchterme ist ein weiterer Bruchterm, dessen Zähler das Produkt aus den Zählern und dessen Nenner das Produkt aus den Nennern ist

Um zu vereinfachen, zerlegen wir in Faktoren

Wir klammern den gemeinsamen Faktor [/latex] aus dem ersten Faktor des Zählers aus. Der zweite Faktor ist ein perfektes quadratisches Trinom, das wir in ein Binom zum Quadrat umwandeln könnnen. Wir erhalten somit

und

Wir faktorisieren das Trinom des Nenners mithilfe der abc-Formel

Somit gilt

Wir formen weiter um

Wir setzen alles in unsere Multiplikation ein und erhalten

Wir vereinfachen

Wir multiplizieren die Nenner und Zähler und erhalten dadurch

Das erste Trinom des Zähler ist ein perfektes quadratisches Trinom. Es entspricht einem Binom zum Quadrat.

Das zweite Trinom faktorisieren wir mithilfe der abc-Formel.

Im ersten Binom des Nenners haben wir unterschiedliche Hochzahlen. Wir faktorisieren.

Wir klammern den gemeinsamen Faktor aus dem zweiten Binom aus. Schließlich sieht unsere Multiplikation wie folgt aus

Wir vereinfachen

Die Division von zwei Bruchtermen ist ein weiterer Bruchterm, dessen Zähler das Produkt aus dem Zähler des ersten Bruchterms und dem Nenner des zweiten Bruchterms ist. Der Nenner ist das Produkt aus dem Nenner des ersten Bruchterms und dem Zähler des zweiten Bruchterms.

Das zweite Binom ist eine Summe hoch 3:

Das Trinom des Nenners ist ein perfektes quadratisches Trinom. Das Binom hat unterschiedliche Hochzahlen und wir faktorisieren deshalb.

Wir vereinfachen

oder auch

Durch die Divison erhalten wir

Der erste Faktor kann mithilfe des Restsatzes und des Horner Schemas zerlegt werden.

Wir klammern den gemeinsamen Faktor aus und es bleibt ein perfektes quadratisches Trinom, das wir auch als Binom zum Quadrat schreiben können.

Der erste Faktor des Nenners ist ein Trinom zweiten Grades, das wir mithilfe der allgemeinen Formel faktorisieren können.

Wir klammern den gemeinsamen Faktor aus. Unser ursprünglicher Ausdruck sieht nun wie folgt aus

wir vereinfachen

Wir multiplizieren Nenner und Zähler mit und erhalten somit einen äquivalenten Bruchterm

Wir vereinfachen

Löse:

Wir haben das Produkt aus einer Summe und einer Differenz. Dies drücken wir als eine Differenz zum Quadrat aus. Wir erhalten

Wir bringen auf einen gemeinsamen Nenner

Wir klammern den gemeinsamen Faktor aus und fahren fort

Wir multiplizieren

Führe aus:

Wir bringen auf einen gemeinsamen Nenner

Die Division der zwei Bruchterme ergibt einen weiteren Bruchterm. Dessen Zähler ist das Produkt aus dem Zähler des ersten Bruchterms und dem Nenner des zweiten Bruchterms. Der Nenner ist das Produkt aus dem Nenner des ersten Bruchterms und dem Zähler des zweiten Bruchterms.

Wir vereinfachen

Führe aus:

Als Erstes addieren wir und nehmen den Kehrwert des Ergebnisses. Dies wiederholen wir so lange, bis wir unser Ergebnis erhalten.