Kapitel
In diesem Abschnitt befassen wir uns mit der Definition des Monoms, seinen Eigenschaften, den dazugehörigen Regeln und einigen Rechenoperationen.

Was ist ein Monom?
Ein Monom ist in der Algebra ein eingliedriger Term, der sich aus dem Produkt von unbekannten Variablen, deren Exponenten ganze, nicht negative Zahlen sind, und einer Zahl, dem Koeffizienten, zusammensetzt. Jedes Polynom ist eine Summe von Monomen. Deshalb können wir ein Monom wie ein Polynom, dass nur einen Term hat, behandeln.
Der Grad des Monoms ist immer die höchste Potenz der Variablen.
Beispiele für Monome sind 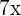 . Die Unbekannte ist
. Die Unbekannte ist  , der Koeffizient ist
, der Koeffizient ist  und der Grad des Monoms ist
und der Grad des Monoms ist  . Ein weiteres Beispiel ist
. Ein weiteres Beispiel ist 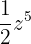 . Die Unbekannte ist
. Die Unbekannte ist  , der Koeffizient ist
, der Koeffizient ist  und der Grad des Monoms ist
und der Grad des Monoms ist  . Ein letztes Beispiel ist
. Ein letztes Beispiel ist 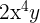 mit den Variablen
mit den Variablen  und
und  . Der Koeffizient ist
. Der Koeffizient ist  und der Grad des Monoms ist
und der Grad des Monoms ist  .
. 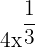 hingegen ist kein Monom, da sein Exponent ein Bruch ist. Dies gilt auch für
hingegen ist kein Monom, da sein Exponent ein Bruch ist. Dies gilt auch für 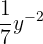 , da der Exponent negativ ist.
, da der Exponent negativ ist.
Bestimme, welche der folgenden algebraischen Ausdrücke Monome sind. Bestimme auch den Grad und den jeweiligen Koeffizienten.
1 
2 
3 
4 
5 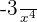
6 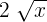
Wir analysieren, ob die Ausdrücke der Definition entsprechen und bestimmen so den Grad und den Koeffizienten.
1 
Hierbei handelt es sich um ein Monom. Da es außerdem nur eine Variable gibt und ihre Potenz  ist, ist der Grad des Monoms
ist, ist der Grad des Monoms  und der Koeffizient ist auch
und der Koeffizient ist auch  .
.
2 
Die Potenz der Variablen  ist
ist  , deswegen trifft die Definition eines Monoms hier nicht zu, da keine negativen Potenzen enthalten sein dürfen.
, deswegen trifft die Definition eines Monoms hier nicht zu, da keine negativen Potenzen enthalten sein dürfen.
3 
Hierbei handelt es sich nicht um ein Monom, da sich ein Monom aus nur einem Term zusammensetzt. Hier haben wir aber zwei Terme,  und
und  . Somit handelt es sich hier um ein Binom.
. Somit handelt es sich hier um ein Binom.
4 
Hierbei handelt es sich um ein Monom. Der Grad ist  , da der Exponent von
, da der Exponent von 
 ist. Der Koeffizient ist
ist. Der Koeffizient ist  .
.
5 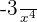
Hierbei handelt es sich nicht um ein Monom, da der Ausdruck 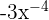 entspricht, dessen Exponent negativ ist.
entspricht, dessen Exponent negativ ist.
6 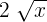
Hierbei handelt es sich nicht um ein Monom, da der Ausdruck 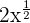 entspricht, dessen Exponent keine ganze Zahl ist. Wir erinnern uns daran, dass der Exponent eine ganze Zahl sein muss und nicht negativ sein darf.
entspricht, dessen Exponent keine ganze Zahl ist. Wir erinnern uns daran, dass der Exponent eine ganze Zahl sein muss und nicht negativ sein darf.
Grundlegende Rechenoperationen bei Monomen
Summe und Differenz
Um zwei Monome zu addieren oder zu subtrahieren und die Terme zusammenzufassen, müssen die vorkommenden Variablen gleich sein und die gleichen Potenzen haben. Das Ergebnis der Summe oder Differenz ist ein Monom, dessen Koeffizient die Summe oder Differenz der Koeffizienten ist, die durch Multiplikation der Unbekannten mit den jeweiligen Potenzen addiert oder subtrahiert werden. Zum Beispiel kann die Summe 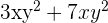 vereinfacht werden, da die Variablen gleich sind,
vereinfacht werden, da die Variablen gleich sind,  und
und  . Außerdem haben diese die gleichen Potenzen,
. Außerdem haben diese die gleichen Potenzen,  hat die Potenz
hat die Potenz  und
und  Potenz
Potenz  bei beiden Monomen. Deshalb entpricht die Summe
bei beiden Monomen. Deshalb entpricht die Summe
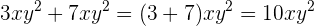
Andererseits kann die Summe  nicht vereinfacht werden, da die Potenzen der Variablen
nicht vereinfacht werden, da die Potenzen der Variablen  nicht gleich sind. Deshalb können wir die Summe nur als
nicht gleich sind. Deshalb können wir die Summe nur als  ausdrücken. Die Variable
ausdrücken. Die Variable  der Monome können wir bestimmen. Allerdings behandeln wir dieses Thema nicht in diesem Artikel.
der Monome können wir bestimmen. Allerdings behandeln wir dieses Thema nicht in diesem Artikel.
Multiplikation und Division
Wir wissen bereits, dass, wenn wir zwei Terme mit der gleichen Basis multiplizieren, wir als Ergebnis die Basis hoch die Summe der Potenzen erhalten. Anders formuliert, das Produkt aus den Ausdrücken  und
und  mit der gleichen Basis ist
mit der gleichen Basis ist
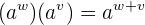
So ist, zum Beispiel, das Produkt von  und
und 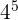
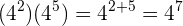
Mit Monomen verhält es sich nun ganz ähnlich. Wenn man zwei Monome multipliziert, ist der daraus resultierende Koeffizient das Produkt der jeweiligen Koeffizienten. Bei den Variablen fassen wir diejenigen mit gleicher Basis zusammen und multiplizieren dementsprechend. Falls es Variablen gibt, die nur in einem Monom auftauchen, aber nicht im anderen, gehen wir wie im folgenden Beispiel vor. Das Produkt der Monome  und
und 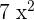 ist
ist

Analog dazu wissen wir, dass, wenn wir zwei Terme mit gleicher Basis dividieren, wir als Ergebnis die Basis hoch die Differenz der Potenzen (die Potenz des Zählers minus die Potenz des Nenners) erhalten. Anders formuliert, die Division der Ausdrücke mit der gleichen Basis  und
und  ist
ist
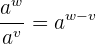
So ist zum Beispiel das Produkt aus  und
und 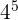

Mit Monomen verhält es sich ganz ähnlich. Wenn man zwei Monome dividiert, ist der resultierende Koeffizient die Division der jeweiligen Koeffizienten. Bei den Variablen fassen wir diejenigen mit gleicher Basis zusammen und dividieren entsprechend. Wenn es Variablen gibt, die im Zähler stehen, aber nicht im Nenner, schreiben wir sie direkt neben den Bruch. Wenn es jedoch Variablen gibt, die im Nenner stehen, aber nicht im Zähler, schreiben wir sie neben den Bruch, müssen aber das Vorzeichen der Potenz umdrehen. Zum Beispiel die Monome  und
und 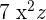 , deren Division ist
, deren Division ist
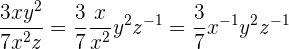
Monome potenzieren
Die Potenzen von Monomen sind einfach. Beim Potenzieren von Monomen wird jeder Faktor separat potenziert und die Exponenten der Variablen werden mit dem Exponenten multipliziert. Selbstverständlich müssen die Regeln für Exponenten eingehalten werden. Wenn wir also zum Beispiel das Monom  auf die Potenz
auf die Potenz  bringen möchten, müssen wir
bringen möchten, müssen wir

Übungsaufgaben zum Rechnen mit Monomen
Übungsaufgaben zu Summen und Differenzen
Übungsaufgaben zu Summen und Differenzen
1 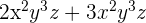
2 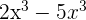
3 
4 
Um diese Aufgaben zu lösen, wenden wir die Regeln zum Umgang mit Summen und Differenzen bei Monomen an, die wir vorher schon behandelt haben.
1 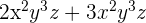
Da beide Monome die gleichen Variablen mit der selben Potenz haben, können wir direkt vereinfachen
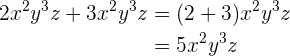
2 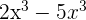
Da beide Monome die gleichen Variablen mit den gleichen Potenzen haben, können wir direkt vereinfachen
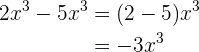
3 
Uns fällt auf, dass alle Monome die gleichen Variablen haben. Allerdings haben nur zwei Monome Variablen mit den gleichen Potenzen. Deshalb können nur diese beiden vereinfacht werden
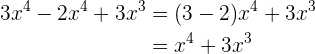
4 
Wir stellen fest, dass alle Monome die gleichen Variablen haben. Allerdings haben sie nicht alle die gleiche Potenz. Wir fassen die Monome mit den gleichen Variablen und Potenzen zusammen und vereinfachen somit
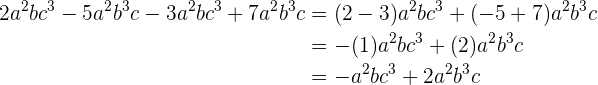
Übungsaufgaben zum Produkt von Monomen
1 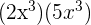
2 
3 
4 
5 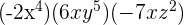
Um diese Aufgaben zu lösen, wenden wir die Regeln für das Produkt von Monomen an, die wir vorher behandelt haben. Wir fassen gleiche Variablen und Koeffizienten zusammen.
1 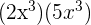
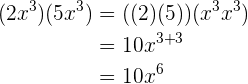
2 
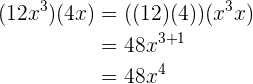
3 
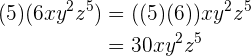
4 
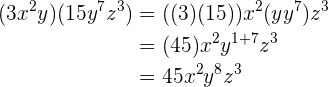
5 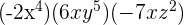
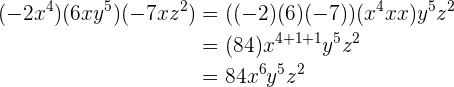
Übungsaufgaben zur Division von Monomen
1 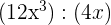
2 
3 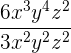
4 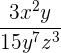
5 
Um diese Aufgaben zu lösen, wenden wir die Regel für die Division von Monomen an. Wir fassen gleiche Variablen und Koeffizienten zusammen.
1 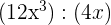
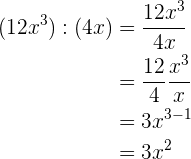
2 
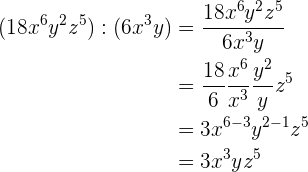
3 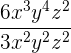
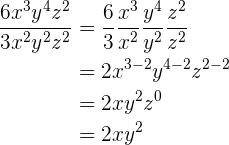
4 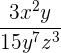
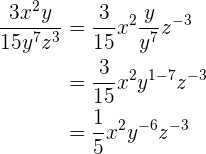
5 
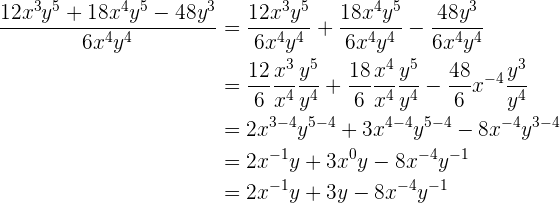
Übungsaufgaben zu Potenzen von Monomen
1 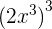 <
<
2 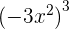
3 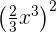
Um diese Aufgaben zu lösen, wenden wir die Regel für das Potenzieren von Monomen an, die wir bereits behandelt haben. Variablen und Koeffizienten müssen entsprechend potenziert werden.
1
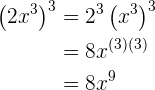
2
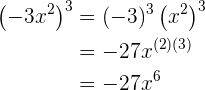
3
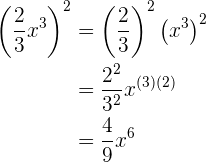
Mit KI zusammenfassen:













