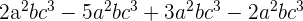
Die Monome, aus denen sich der mathematische Ausdruck zusammensetzt, sind äquivalent. Das heißt, sie haben dieselben Variablen mit den jeweiligen Exponenten. Deshalb erhält man das Ergebnis, indem man die Koeffizienten zusammenfasst und die Variablen mit den jeweiligen Exponenten beibehält
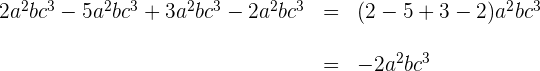

Um zwei Monome zu dividieren, dividieren wir deren Koeffizenten und wenden die Regeln für die Exponenten bei den Variablen an: Um zwei Elemente mit der gleichen Basis zu dividieren, behält man die Basis bei und subtrahiert die Exponenten
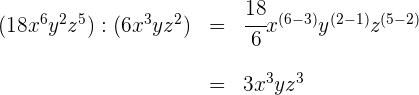
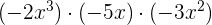
Um Monome miteinander zu multiplizieren, multiplizieren wir deren Koeffizienten und wenden die Regeln für die Exponenten der Variablen an: Um Elemente mit der gleichen Basis zu multiplizieren, behält man die Basis bei und addiert die Exponenten


Um zwei Monome zu dividieren, dividieren wir deren Koeffizienten und wenden die Regel für die Exponenten der Variablen an: Um zwei Elemente mit der gleichen Basis zu dividieren, behält man die Basis bei und subtrahiert die Exponenten
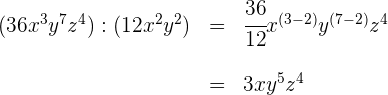

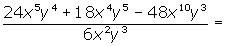
1
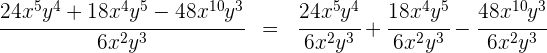
2
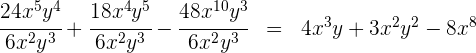
Folgende Polynome sind gegeben:
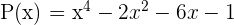

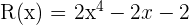
Wir berechnen:
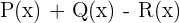
1
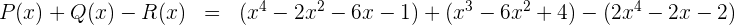
2

3
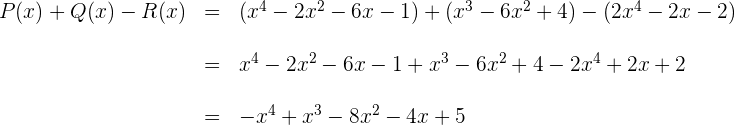
Folgende Polynome sind gegeben:
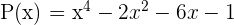

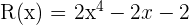
Wir berechnen:

1
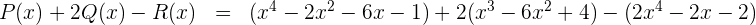
2

3
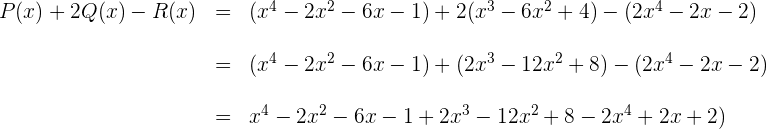
4
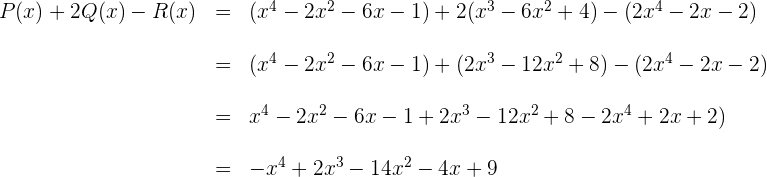
Folgende Polynome sind gegeben:
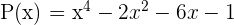

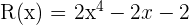
Wir berechnen:

1

2
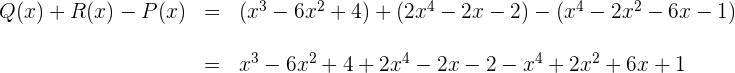
3

Berechne den Wert für  , damit die Gleichung stimmt:
, damit die Gleichung stimmt:

1
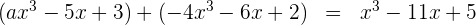
2
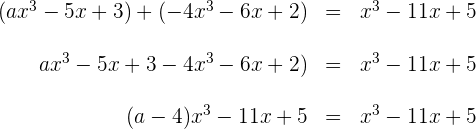
3
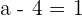 ,
, 
Multiplikation 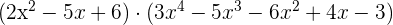
1
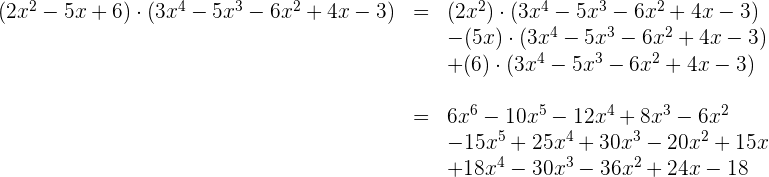
2

Den numerischen Wert des Polynoms 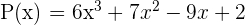 finden, für:
finden, für: 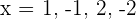
1
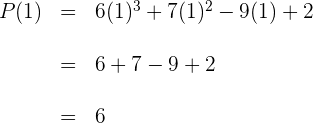
2
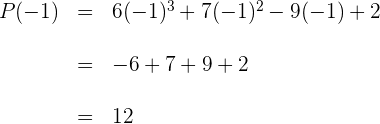
3
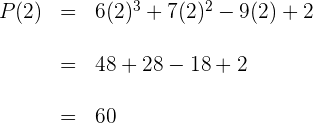
4

Berechne:
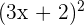
1

2

Berechne:
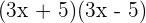
1
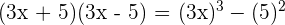
2
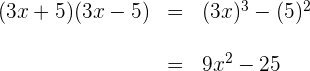
Mit KI zusammenfassen:



