Kapitel
Ein Bruchterm ist der Quotient zweier Polynome und sieht wie folgt aus:
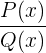
Hierbei gilt:
 ist der Zähler,
ist der Zähler,
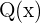 ist der Nenner,
ist der Nenner,
Es muss gelten 
Beispiele:
1 
2 
3 

Äquivalente Bruchterme
Zwei Bruchterme

sind äquivalent und können wie folgt dargestellt werden:
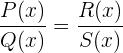
wenn gilt
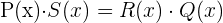
Beispiel:
Überprüfen, ob die Bruchterme äquivalent sind
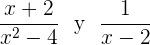
Wir überprüfen, ob wir auf beiden Seiten das gleiche Ergebnis erhalten
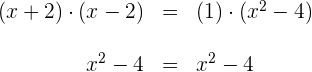
Beide Produkte sind gleich, deshalb sind die Bruchterme äquivalent
Aufbau von äquivalenten Bruchtermen
Wir haben einen Bruchterm. Wenn wir dessen Zähler und Nenner mit einem gleichen Polynom, das nicht null ist, multiplizieren, ist der resulitierende Bruchterm äquivalent zu dem gegebenen Bruchterm.
Beispiel:
Wenn wir den Zähler und den Nenner des Bruchterms

mit 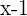 multiplizieren, erhalten wir einen äquivalenten Bruchterm
multiplizieren, erhalten wir einen äquivalenten Bruchterm
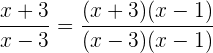
Um zu überprüfen, ob sie äquivalent sind, multiplizieren wir wie folgt
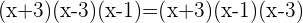
Da auf beiden Seiten die gleichen Faktoren stehen, ist die Gleichung allgemein gültig. Das heißt, die beiden Bruchterme sind äquivalent.
Bruchterme vereinfachen
Um Bruchterme zu vereinfachen, teilt man den Zähler und den Nenner des Bruchs durch ein Polynom, das von beiden ein Faktor ist.
Beispiel:
Vereinfachen 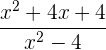
1 Wir faktorisieren den Zähler, der ein vollständiges quadratisches Trinom ist
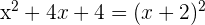
2 Wir faktorisieren den Nenner, der eine Differenz von Quadraten ist
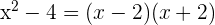
3 Durch den gemeinsamen Faktor  vereinfachen wir und erhalten
vereinfachen wir und erhalten

Beispiel:
Wir vereinfachen 
1Wir faktorisieren den Zähler, der einen gemeinsamen Faktor und eine Differenz von Quadraten enthält
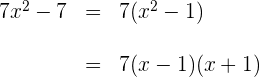
2Wir faktorisieren den Nenner, der einen gemeinsamen Faktor und eine Differenz von Kubikzahlen enthält
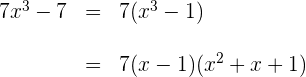
3Mit dem gemeinsamen Faktor 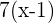 vereinfachen wir und erhalten
vereinfachen wir und erhalten

Bruchterme erweitern
Um einen Bruchterm zu erweitern, multipliziert man den Zähler und den Nenner mit einem gleichen Polynom.
Beispiel:

Mit KI zusammenfassen:













