Polynome addieren
Um eine Summe aus zwei oder mehr Polynomen zu erhalten, müssen die Koeffizienten der Terme, deren Unbekannte gleich sind, addiert werden. Das heißt, die Variablen und Exponenten der zu addierenden Terme müssen gleich sein.
Methode 1 zur Addition von Polynomen
Schritte:
1 Polynome nach absteigendem Grad ordnen.
2 Monome vom selben Grad zusammenfassen.
3 Gleichartige Monome addieren.
Beispiel 1 zur Addition von Polynomen
Polynome addieren
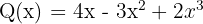
1 Wir ordnen die Polynome, falls sie es noch nicht sind.
2 Wir fassen die Monome vom selben Grad zusammen.
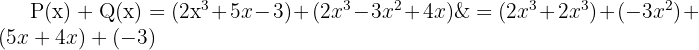
3 Wir addieren gleichartige Monome.
Methode 2 zur Addition von Polynomen
Wir können Polynome auch addieren, indem wir sie einfach untereinander schreiben. Und zwar so, dass sich die gleichartigen Monome in Spalten befinden und sich somit addieren lassen.
Beispiel für Methode 2
Addiere folgende Polynome
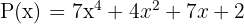
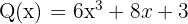
1Wir schreiben die Terme in absteigende Reihenfolge in Spalten und addieren.
Somit
2 
Polynome subtrahieren
Bei der Polynomsubtraktion wird das Gegenteil des Subtrahenden zum Minuenden addiert.
Beispiel für die Polynomsubtraktion
Subtrahiere folgende Polynome
1 Wir erhalten das Gegenteil des Subtrahenden 
.
2 Wir fassen zusammen.
3 Ergebnis der Subtraktion.
Polynome multiplizieren
1. Eine Zahl mit einem Polynom multiplizieren
Die Multiplikation einer Zahl mit einem Polynom ergibt ein weiteres Polynom. Das erhaltene Polynom hat den gleichen Grad wie das Ausgangspolynom. Die Koeffizienten des resultierenden Polynoms sind das Produkt aus den Koeffizienten des Ausgangspolynoms und der Zahl, die vor der Klammer steht. Die Variablen bleiben gleich.
Beispiele:
1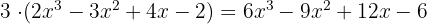 
2 
2. Ein Monom mit einem Polynom multiplizieren
Bei der Multiplikation eines Monoms mit einem Polynom wird das Monom mit jedem einzelnen Monom des Polynoms multipliziert.
Wir denken daran, dass wir zuerst immer die Vorzeichen multiplizieren müssen, bevor wir die dazugehörigen Monome multiplizieren. Dazu müssen die Koeffizienten und schließlich die Unbekannte multipliziert werden. Hierbei werden bei der Multiplikation von gleichen Variablen die Exponenten addiert.
Beispiel:
3. Polynome multiplizieren
Diese Rechenoperation kann auf unterschiedliche Arten erfolgen.
Methode 1 zur Multiplikation von Polynomen
Schritte:
1 Jedes Monom des ersten Polynoms wird mit allen Elementen des zweiten Polynoms multipliziert.
2 Monome vom selben Grad werden addiert und man erhält ein anderes Polynom, dessen Grad die Summe aus den Graden der Polynome ist, die multipliziert werden.
Beispiel:
Multipliziere folgende Polynome
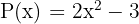
1Jedes Monom des ersten Polynoms wird mit allen Elementen des zweiten Polynoms multipliziert.
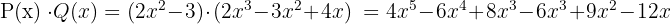
2Polynome vom selben Grad werden addiert.
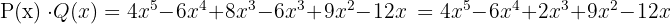
3 Wir erhalten ein anderes Polynom, dessen Grad die Summe der Grade der Polynome ist, die multipliziert werden.
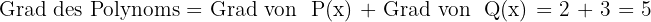
und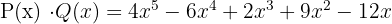
Methode 2 zur Multiplikation von Polynomen
Wir können Polynome auch multiplizieren, indem wir sie untereinander schreiben. In jeder Zeile wird jedes Monom des zweiten Polynoms mit allen Monomen des ersten Polynoms multipliziert. Gleichartige Monome werden in der gleichen Spalte zusammengefasst und schließlich werden die gleichartigen Monome addiert.
Beispiel:
Multipliziere folgende Polynome
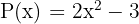
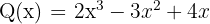
Da für die Multiplikation von Polynomen das Kommutativgesetz gilt, nehmen wir als Polynom, mit dem wir multiplizieren, das einfachste Polynom.
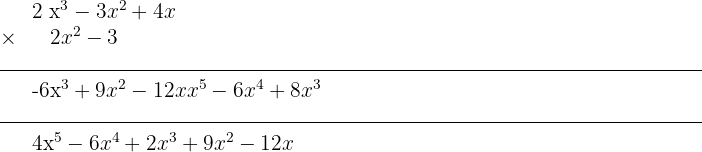
Polynome dividieren
Wir beginnen die Erklärung mit einem Beispiel.
Beispiel:
Dividiere folgende Polynome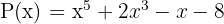
P(x) : Q(x)
1 Auf der linken Seite platzieren wir den Dividenen. Sollte das Polynom nicht vollständig sein, lassen wir an den entsprechenden Stellen eine Lücke.
2 Den Divisor schreiben wir rechts in eine Box.
3 Wir dividieren das erste Monom des Dividenden durch das erste Monom des Divisors.
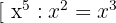
4 Wir multiplizieren jeden Term des Polynoms des Divisors durch das vorhergehende Ergebnis und subtrahieren es vom Polynom des Dividenden:
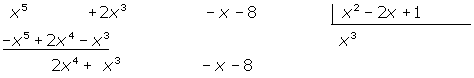
5 Wir dividieren noch einmal das erste Monom des Dividenden durch das erste Monom des Divisors. Das Ergebnis multiplizieren wir mit dem Divisor und subtrahieren es vom Dividenden.
wir erhalten
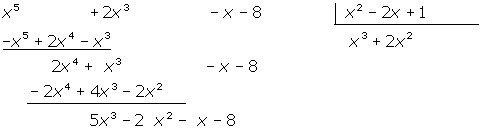
6 Wir gehen genauso vor wie zuvor. Und dieses Mal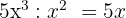 
also
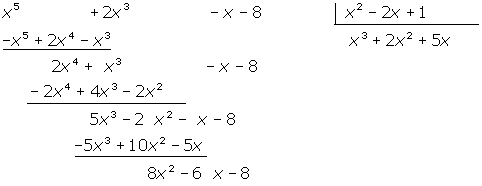
7 Wie bei den vorhergehenden Schritten dividieren wir 
durch 
und erhalten 
. Wir multiplizieren jeden Term des Divisors mit und erhalten:
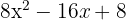
Mit dem Rest verfahren wir wie folgt:
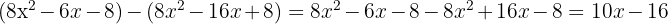
Wir stellen fest, dass 10x − 16 der Rest ist, da sein Grad niedriger ist als der des Divisors. Wir können deshalb nicht weiter dividieren. Der Quotient ist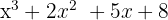 
Du brauchst Nachhilfe in Mathe ? Bei Superprof findest du Matheprofis in deiner Nähe!
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
