Kapitel

Definition der Ähnlichkeit von Dreiecken
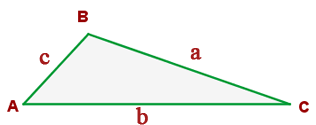
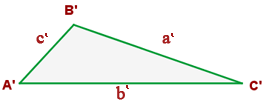
Gegeben sind die Dreiecke  und
und 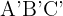 , die Seiten
, die Seiten  und
und  ,
,  und
und  ,
,  und
und  werden homologe Seiten genannt. Die homologen Winkel sind:
werden homologe Seiten genannt. Die homologen Winkel sind: 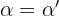 ,
,  y
y 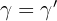 . Zwei Dreiecke sind ähnlich, wenn ihre homologen Winkel gleich und ihre homologen Seiten proportional sind. Das bedeutet folgendes:
. Zwei Dreiecke sind ähnlich, wenn ihre homologen Winkel gleich und ihre homologen Seiten proportional sind. Das bedeutet folgendes:
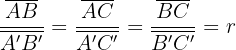
und

Das Verhältnis der Proportionen  zwischen den homologen Seiten von Dreiecken wird als Ähnlichkeitsverhältnis bezeichnet.
zwischen den homologen Seiten von Dreiecken wird als Ähnlichkeitsverhältnis bezeichnet.
Beobachtungen:
1. Das Verhältnis der Umfänge von ähnlichen Dreiecken ist gleich ihrem Ähnlichkeitsverhältnis.
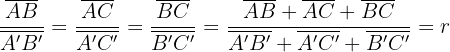
2. Das Verhältnis der Flächen ähnlicher Dreiecke ist gleich dem Quadrat ihres Ähnlichkeitsverhältnisses. Wenn also die Flächen der Dreiecke  und
und 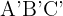 jeweils
jeweils  und
und 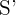 sind, dann gilt:
sind, dann gilt:
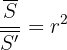
Praktische Beispiele
1 Berechne die Höhe eines Gebäudes, das einen Schatten von 6,5 m wirft, während ein 4,5 m hoher Mast zur gleichen Zeit einen Schatten von 0,90 m wirft.
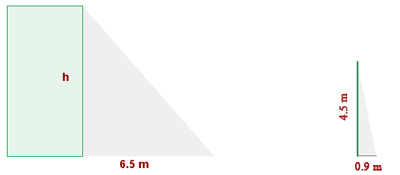
Da die Schatten zur gleichen Zeit geworfen werden, stützt du dich auf die Ähnlichkeit, um eine Lösung anzugeben. Aufgrund der Ähnlichkeit hast du also folgende Gleichheit

durch Auflösen nach  erhältst du
erhältst du
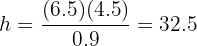
2 Die Katheten eines rechtwinkligen Dreiecks messen 24 m und 10 m. Wie lang sind die Katheten eines ähnlichen Dreiecks, dessen Hypotenuse 52 m misst?
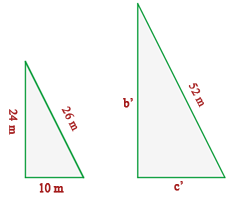
Da du die Katheten eines der rechtwinkligen Dreiecke kennst, kannst du seine Hypotenuse berechnen
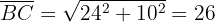
Da die Hypotenuse bereits gegeben ist und die Dreiecke ähnlich sind, kannst du die Tatsache nutzen, dass die Seiten proportional sind, um die Katheten des anderen Dreiecks zu erhalten. Berechne zunächst  .
.

nach Auflösen von  erhältst du
erhältst du
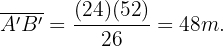
Berechne jetzt 
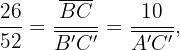
nach Auflösen von  erhältst du
erhältst du

Kriterien für Ähnlichkeit
Gleiche Winkel
Zwei Dreiecke sind ähnlich, wenn sie zwei gleiche Winkel haben.
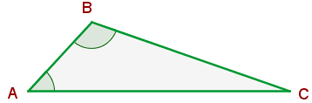
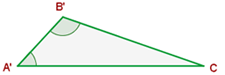

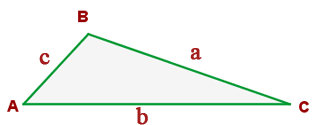
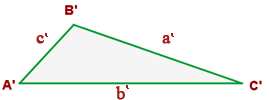
Proportionale Seiten
Zwei Dreiecke sind ähnlich, wenn ihre Seiten proportional sind.
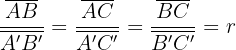
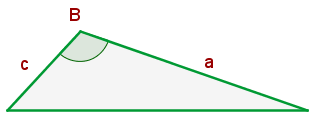
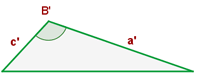
Winkel zwischen den Seiten
Zwei Dreiecke sind ähnlich, wenn sie zwei proportionale Seiten haben und die Winkel zwischen ihnen gleich sind.
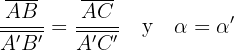
oder auch
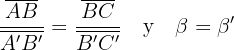
oder auch
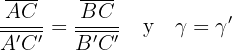
Beispiele
Zeige, dass die beiden Dreiecke ähnlich sind:
1
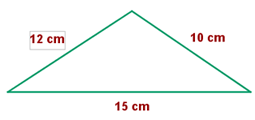
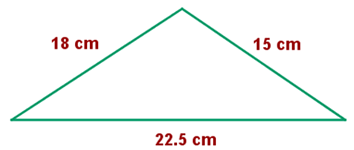
Für dieses Beispiel analysierst du, ob die Seiten proportional sind. Dafür kannst du auf mehrere Arten vorgehen. Am besten reduzierst du die Proportion jeder Seite auf ihren minimalen Wert und überprüfst, ob sie übereinstimmen. Wenn ja, hast du das Verhältnis der Proportion  gefunden. Dabei musst du beachten, dass
gefunden. Dabei musst du beachten, dass
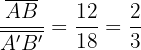 ,
,
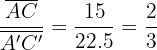 ,
,
und zuletzt
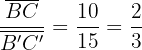 .
.
Du erhältst also

Du kannst darauf schließen, dass die Dreiecke ähnlich sind, weil ihre Seiten proportional sind.
2
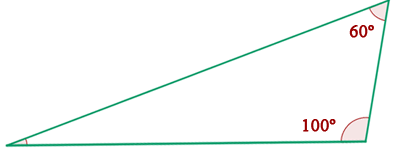
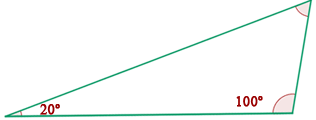
Erinnere dich, dass die Summe der Innenwinkel eines Dreiecks immer gleich  ist. Das heißt folgendes:
ist. Das heißt folgendes:
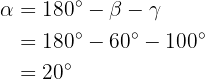
Beachte nun, dass  y
y  . Daher sind sie ähnlich, weil sie zwei gleiche Winkel haben.
. Daher sind sie ähnlich, weil sie zwei gleiche Winkel haben.
3
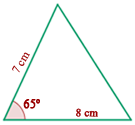
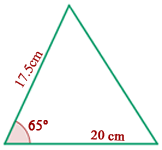
Überprüfe, ob die beiden Seiten der Dreiecke proportional und ob die Winkel zwischen ihnen gleich sind. Beachte, dass  .
.
Daher sind sie ähnlich, weil sie zwei gleiche Winkel haben. Dann musst du nur noch überprüfen, dass die Seiten proportional sind. Du stellst fest, dass
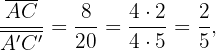
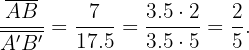
Daher musst du

Die beiden Dreiecke sind also ähnlich, weil sie zwei proportionale Seiten haben und die Winkel zwischen ihnen gleich sind.
Ähnlichkeit von rechtwinkligen Dreiecken
Winkel
Zwei rechtwinklige Dreiecke sind ähnlich, wenn sie einen Winkel (außer dem rechten Winkel) gleich haben.
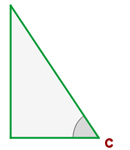
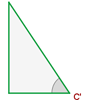
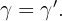
Proportionale Katheten
Zwei rechtwinklige Dreiecke sind ähnlich, wenn ihre beiden Seiten proportional sind.
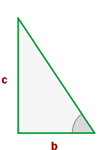
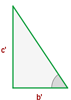

Hypotenuse und Kathete
Zwei rechtwinklige Dreiecke sind ähnlich, wenn die Hypotenuse und eine Kathete proportional sind.
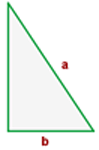
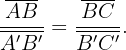
Mit KI zusammenfassen:













