Die Hypotenuse eines rechtwinkligen Dreiecks misst 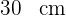 und die Abbildung einer Kathete auf sie misst
und die Abbildung einer Kathete auf sie misst 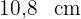 . Ermittle die Kathete
. Ermittle die Kathete  .
.
1 Wir stellen das Problem grafisch dar
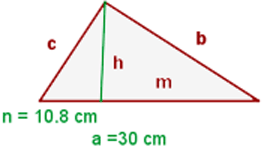
2 Wir stellen fest, dass sich zwei äquivalente Dreiecke ergeben, so dass wir Folgendes erhalten
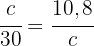
3 Wir lösen nach  auf und erhalten
auf und erhalten
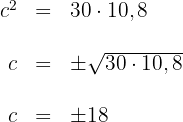
4 Da die Abstände nicht negativ sein können, ist der Wert der geforderten Kathete 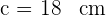
In einem rechtwinkligen Dreieck messen die Abbildungen der Schenkel auf die Hypotenuse  und
und  Meter. Berechne die relative Höhe zur Hypotenuse.
Meter. Berechne die relative Höhe zur Hypotenuse.
1 Wir stellen das Problem grafisch dar
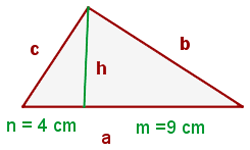
2 Wir stellen fest, dass wir zwei äquivalente Dreiecke erhalten. Somit ergibt sich
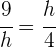
3 Wir lösen nach  auf und erhalten
auf und erhalten
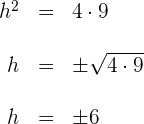
4 Da die Abstände nicht negativ sein können, ist der gesuchte Wert 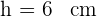
Die Hypotenuse eines rechtwinkligen Dreiecks misst 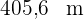 und die Abbildung einer Kathete auf sie
und die Abbildung einer Kathete auf sie  . Berechne die Katheten und die relative Höhe zur Hypotenuse.
. Berechne die Katheten und die relative Höhe zur Hypotenuse.
1 Wir stellen das Problem grafisch dar
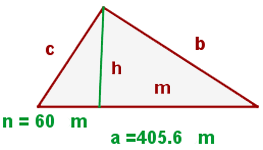
2 Wir stellen fest, dass wir zwei äquivalente Dreiecke erhalten. Da die Hypotenuse 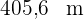 und die Abbildung einer Kathete
und die Abbildung einer Kathete  misst, haben wir
misst, haben wir
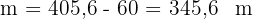
3 Für die Kathete  gilt
gilt
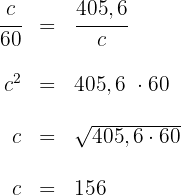
4 Für die Kathete  gilt
gilt
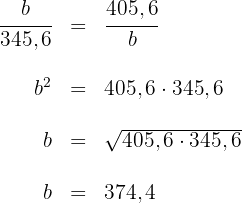
5 Für die Höhe  gilt
gilt
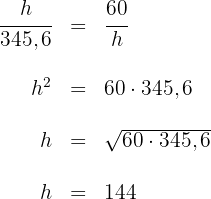
Berechne die Seiten eines rechtwinkligen Dreiecken, wenn du weißt, dass die Abbildung einer der Katheten auf die Hypotenuse  misst und die relative Höhe
misst und die relative Höhe 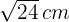 misst.
misst.
1 Wir stellen das Problem grafisch dar
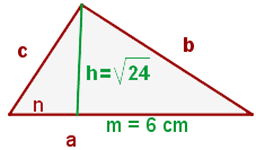
2 Wir stellen fest, dass wir zwei äquivalente Dreiecke erhalten. Somit ergibt sich
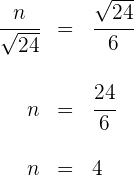
Also misst die Hypotenuse

3 Für die Kathete  gilt
gilt
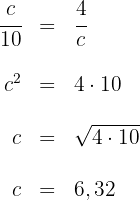
4 Für die Kathete  gilt
gilt
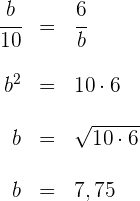
5 Somit sind die Seiten des Dreiecks: 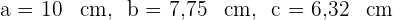
Eine Leiter mit einer Länge von  ist an eine Wand gelehnt. Der Fuß der Leiter befindet sich
ist an eine Wand gelehnt. Der Fuß der Leiter befindet sich  von der Wand entfernt. In welcher Höhe berührt die Leiter die Wand?
von der Wand entfernt. In welcher Höhe berührt die Leiter die Wand?
1 Wir stellen das Problem grafisch dar
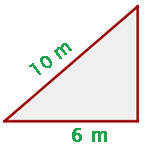
2 Wir stellen fest, dass die Höhe der Leiter an der Wand durch den Satz des Pythagoras gegeben ist
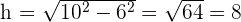
3 Somit ist die gesuchte Höhe 
Bestimme die Seite eines gleichseitigen Dreiecks, dessen Umfang gleich dem eines Quadrats mit einer Seitenlänge von 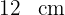 ist. Sind ihre Flächen gleich?
ist. Sind ihre Flächen gleich?
1 Wir stellen das Quadrat grafisch dar

2Sein Umfang ist  . Zur Berechnung der Fläche gehen wir wie folgt vor
. Zur Berechnung der Fläche gehen wir wie folgt vor
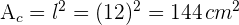
3Das gleichseitige Dreieck hat drei gleiche Seiten. Wenn also sein Umfang 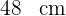 beträgt, dann misst jede seiner Seiten
beträgt, dann misst jede seiner Seiten 
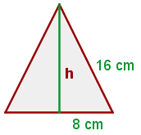
4Um die Fläche zu bestimmen, müssen wir die Höhe kennen. Dazu teilen wir das gleichseitige Dreieck in zwei rechtwinklige Dreiecke und wenden den Satz des Pythagoras an
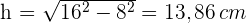
5Um die Fläche zu berechnen, gehen wir wie folgt vor
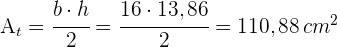
Die beiden Figuren haben also den gleichen Umfang, aber unterschiedliche Flächen.
Berechne die Fläche eines gleichseitigen Dreiecks, das in einen Kreis mit dem Radius  eingeschrieben ist.
eingeschrieben ist.
1 Wir stellen das Problem grafisch dar
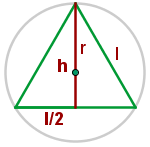
2Der Mittelpunkt des Kreises ist das Baryzentrum, weshalb 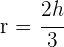 und wir erhalten
und wir erhalten

3Um den Flächeninhalt des Dreiecks zu ermitteln, müssen wir seine Grundseite kennen. Dazu zerlegen wir das gleichseitige Dreieck in zwei rechtwinklige Dreiecke und wenden den Satz des Pythagoras an
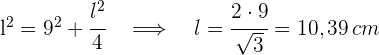
4Um die Fläche zu berechnen, gehen wir wie folgt vor
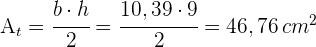
Bestimme die Fläche des Quadrats, das in einen Kreis der Länge 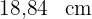 eingeschrieben ist.
eingeschrieben ist.
1 Wir stellen das Problem grafisch dar
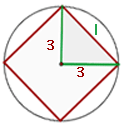
2Wir müssen eine Seite des Quadrats kennen. Dazu berechnen wir zunächst den Radius aus dem Umfang
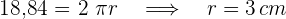
3Um die Seitenlänge des Quadrats zu bestimmen, betrachten wir das gleichschenklige rechtwinklige Dreieck, dessen gleiche Seiten die Radien des Kreisumfangs sind

4Somit ist die Fläche des Quadrats
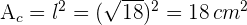
In ein Quadrat mit einer Seitenlänge von  ist ein Kreis eingeschrieben, in diesen Kreis ist ein Quadrat eingeschrieben und in dieses ein weiterer Kreis. Ermittle die Fläche zwischen dem letzten Quadrat und dem letzten Kreis.
ist ein Kreis eingeschrieben, in diesen Kreis ist ein Quadrat eingeschrieben und in dieses ein weiterer Kreis. Ermittle die Fläche zwischen dem letzten Quadrat und dem letzten Kreis.
1 Wir stellen das Problem grafisch dar
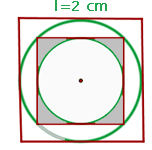
2Wir müssen die Radien der Kreise kennen; Dazu stellen wir fest, dass die Seite des Quadrats der Seitenlänge  gleich dem Durchmesser des Inkreises ist
gleich dem Durchmesser des Inkreises ist
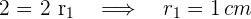
3Der Durchmesser des ersten Kreises ist gleich der Diagonale des zweiten Quadrats. Durch Anwendung des Satzes des Pythagoras erhalten wir die Seitenlänge des zweiten Quadrats

4Die Fläche des zweiten Quadrats beträgt also
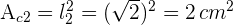
5Der Durchmesser des zweiten Kreises ist gleich der Seite des zweiten Quadrats

6Die Fläche des zweiten Kreises beträgt
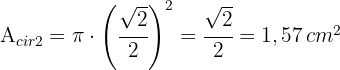
7Die gesuchte Fläche ist also
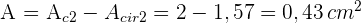
Der Umfang eines gleichschenkligen Trapezes beträgt  , die Grundseiten messen
, die Grundseiten messen  bzw.
bzw.  . Berechne die nicht parallelen Seiten und den Flächeninhalt.
. Berechne die nicht parallelen Seiten und den Flächeninhalt.
1 Wir stellen das Problem grafisch dar
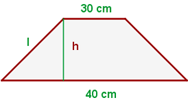
2 Da die Grundseiten sich zu  addieren, ergeben die Seiten
addieren, ergeben die Seiten  , also misst jede Seite
, also misst jede Seite  . Um die Höhe zu ermitteln, konstruieren wir ein rechtwinkliges Dreieck, wie in der Abbildung dargestellt. Nach dem Satz des Pythagoras ergibt sich
. Um die Höhe zu ermitteln, konstruieren wir ein rechtwinkliges Dreieck, wie in der Abbildung dargestellt. Nach dem Satz des Pythagoras ergibt sich
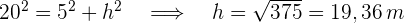
3Wir berechnen den Flächeninhalt des Trapezes
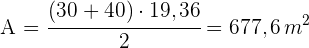
Verlängert man die nicht parallelen Seiten eines gleichschenkligen Trapezes, so entsteht ein gleichseitiges Dreieck mit einer Seitenlänge von  . Berechne den Flächeninhalt des Trapezes, wenn du weißt, dass das Trapez die Hälfte der Höhe des Dreiecks ist.
. Berechne den Flächeninhalt des Trapezes, wenn du weißt, dass das Trapez die Hälfte der Höhe des Dreiecks ist.
1 Wir stellen das Problem grafisch dar
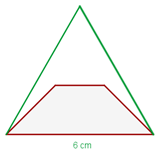
2 Um die Höhe des Dreiecks zu bestimmen, konstruieren wir ein rechtwinkliges Dreieck, dessen Grundseite die Hälfte seiner Höhe misst. Wir wenden den Satz des Pythagoras an und erhalten
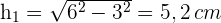
3Wir berechnen die Höhe des Trapezes 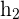
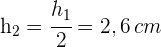
4Wir berechnen den Flächeninhalt des Trapezes
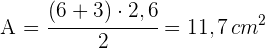
Die Fläche eines Quadrats misst 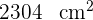 . Berechne die Fläche des regelmäßigen Sechsecks mit demselben Umfang.
. Berechne die Fläche des regelmäßigen Sechsecks mit demselben Umfang.
1 Wir stellen das Problem grafisch dar
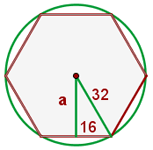
2 Um den Umfang des Quadrats zu kennen, müssen wir den Wert einer seiner Seiten berechnen
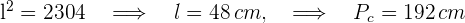
3Wir berechnen das Apothema des Sechsecks und benötigen dazu die Seite des Sechsecks 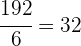
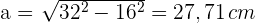
4Wir berechnen den Flächeninhalt des Sechsecks
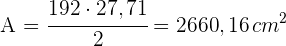
In einen Kreis mit dem Radius 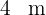 wird ein Quadrat eingeschrieben, und an den Seiten des Quadrats und nach außen werden gleichseitige Dreiecke konstruiert.
wird ein Quadrat eingeschrieben, und an den Seiten des Quadrats und nach außen werden gleichseitige Dreiecke konstruiert.
1 Wir stellen das Problem grafisch dar
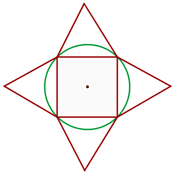
2Wir müssen die Seitenlänge des Quadrats kennen; dazu stellen wir fest, dass der Durchmesser des Kreises gleich der Diagonale des Quadrats ist. Wir wenden den Satz des Pythagoras an und erhalten

3Die Fläche des Quadrats beträgt

4Um den Flächeninhalt des gleichseitigen Dreiecks zu ermitteln, teilen wir es in zwei rechtwinklige Dreiecke und wenden den Satz des Pythagoras an, um die Höhe zu bestimmen
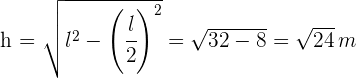
5Der Flächeninhalt des Dreiecks ist
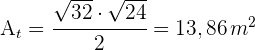
6Die Fläche des Sterns beträgt
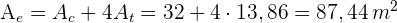
In ein regelmäßiges Sechseck mit einer Seitenlänge von  wird ein Kreis eingeschrieben und es wird von einem anderen Kreis umschrieben. Berechne die Fläche des gebildeten Kreisrings.
wird ein Kreis eingeschrieben und es wird von einem anderen Kreis umschrieben. Berechne die Fläche des gebildeten Kreisrings.
1 Wir stellen das Problem grafisch dar
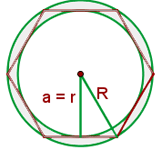
2Wir berechnen den Radius des Umkreises und stellen dazu fest, dass das Sechseck in sechs gleiche gleichseitige Dreiecke unterteilt ist, so dass

3Wir berechnen den Radius des Inkreises, der mit der Höhe des gleichseitigen Dreiecks übereinstimmt.

4Wir berechnen die Fläche des Kreisrings, die sich aus der Differenz der Flächen der Kreise ergibt.
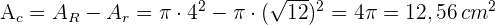
Die Sehne eines Kreises misst 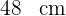 und liegt
und liegt  vom Mittelpunkt entfernt. Berechne die Fläche des Kreises.
vom Mittelpunkt entfernt. Berechne die Fläche des Kreises.
1 Wir stellen das Problem grafisch dar
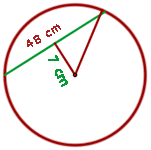
2 Consideramos el triángulo rectángulo como se muestra en la figura y empleando el teorema de Pitágoras, calculamos el radio

3Calculamos el área del círculo
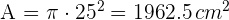
Berechne die Seitenlänge eines gleichseitigen Dreiecks, das in einen Kreis mit dem Radius 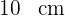 eingeschrieben ist.
eingeschrieben ist.
1 Wir stellen das Problem grafisch dar
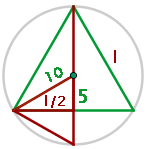
2Wir sehen uns das rechtwinklige Dreieck mit der Seitenlänge  , der Hypotenuse
, der Hypotenuse  und der verbleibenden Seite
und der verbleibenden Seite  an. Mit dem Satz des Pythagoras erhalten wir
an. Mit dem Satz des Pythagoras erhalten wir

Auf einen Kreis mit dem Radius  wird ein Mittelpunktswinkel von
wird ein Mittelpunktswinkel von  gezeichnet. Ermittle die Fläche des Kreissegments zwischen der Sehne, die die Enden der beiden Radien verbindet, und dem entsprechenden Bogen.
gezeichnet. Ermittle die Fläche des Kreissegments zwischen der Sehne, die die Enden der beiden Radien verbindet, und dem entsprechenden Bogen.
1 Wir stellen das Problem grafisch dar
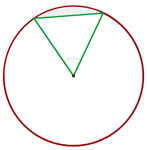
2Die Fläche des Kreissektors ist
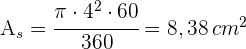
3Um die Höhe des Dreiecks zu bestimmen, wenden wir den Satz des Pythagoras an
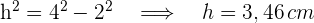
4Wir berechnen den Flächeninhalt des gleichseitigen Dreiecks
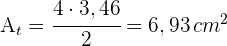
5Die Fläche des Kreissegments ist
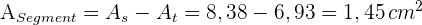
Gegeben ist ein gleichseitiges Dreieck mit einer Seitenlänge von  . Berechne die Fläche eines der Sektoren, die durch den Umkreis und die Radien durch die Eckpunkte bestimmt werden.
. Berechne die Fläche eines der Sektoren, die durch den Umkreis und die Radien durch die Eckpunkte bestimmt werden.
1 Wir stellen das Problem grafisch dar
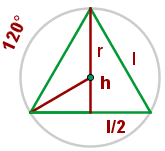
2Der Mittelpunkt des Kreises ist das Baryzentrum, also 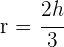
3Um die Höhe des Dreiecks zu bestimmen, wenden wir den Satz des Pythagoras an
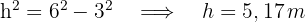
4Wir berechnen den Radius
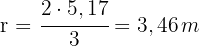
5Die Fläche eines der Sektoren, die durch den Umkreis und die durch die Eckpunkte verlaufenden Radien bestimmt wird, beträgt
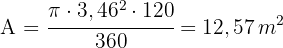
Berechne die Fläche des Kreisrings, die durch den Inkreis und den Umkreis eines Quadrats mit der Diagonale  bestimmt wird.
bestimmt wird.
1 Wir stellen das Problem grafisch dar
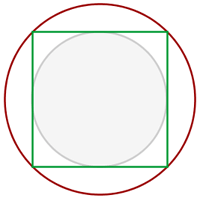
2Wir müssen die Radien der Kreise kennen; dazu stellen wir fest, dass der Durchmesser des Umkreises gleich der Diagonale des Quadrats ist

3Der Durchmesser des Inkreises ist gleich der Seite des Quadrats, und nach dem Satz des Pythagoras erhalten wir

4Die Fläche des Kreisrings ist
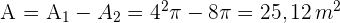
Mit KI zusammenfassen:


