Umfang eines Dreicks
Der UmfangeinesDreiecks entspricht der Summe seiner drei Seiten.
| Gleichseitiges Dreieck | Gleichschenkliges Dreieck | Unregelmäßiges Dreieck |
 |  |  |
 |  |  |
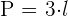Fläche eines Dreiecks
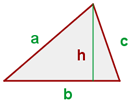
Die Fläche eines Dreiecks lässt sich durch Multiplikation von Grundseite mal Höhegeteilt durch 
berechnen.
Die Höhe ist die senkrechte Gerade, die von einem Eckpunkt zur gegenüberliegendenSeite (oder ihrer Verlängerung) gezogen wird.
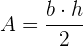
Beispiel zur Flächenberechnung
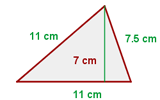
Ermittle die Fläche des folgenden Dreiecks:
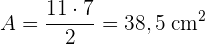
Fläche eines gleichseitigen Dreiecks
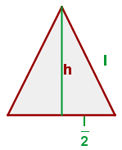
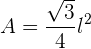
Beispiel für die Berechung der Fläche eines gleichseitigen Dreiecks
Berechne den Flächeninhalt eines gleichseitigen Dreiecks mit einer Seitenlänge von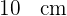 
.
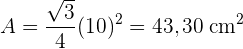
Fläche eines rechtwinkligen Dreiecks
Die Fläche eines rechtwinkligenDreicks berechnet sich durch die Multiplikation der Katheten geteilt durch .
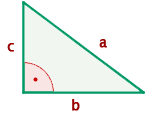
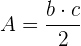
Beispiel für die Berechung der Fläche eines rechtwinkligen Dreiecks
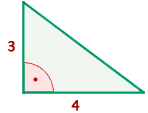
Berechne die Fläche des rechtwinkligenDreiecks, dessen Katheten 
und 
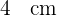lang sind.
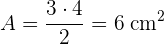
Der halbe Umfang
Der halbeUmfang eines Dreiecks ist die Summe der Seiten geteilt durch .
Die Bezeichnung lautet 
.
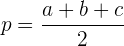
Satz des Heron
Mit dem SatzdesHeron kann man die Fläche eines Dreiecks mittels der dreiSeiten berechnen.
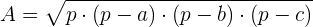
Beispielaufgabe
Berechne die Fläche des Dreiecks, dessen Seiten , 
und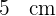 
lang sind.
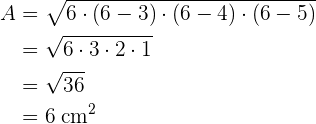
Umkreis eines Dreiecks
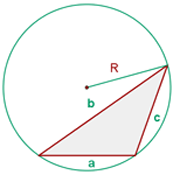
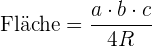
Radius des Umkreises
Inkreis eines Dreiecks
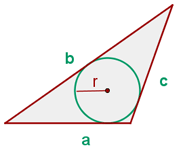
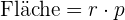
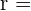Radius des Inkreises
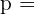halber Umfang
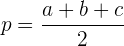
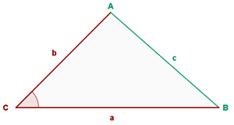
Zwei Seiten und der Winkel, den diese bilden, sind bekannt:
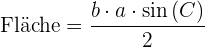
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
