Willkommen in unserem Bereich, der sich mit Problemstellungen zu Flächen befasst. Hier findest du detaillierte Lösungen zu Problemen, die sich auf die Berechnung von Flächen bekannter geometrischer Figuren beziehen. Wir untersuchen die Verwendung spezifischer Formeln und Methoden zur Bestimmung der Flächen von Dreiecken, Quadraten, Kreisen und anderen Figuren.
Jedes gelöste Problem enthält eine schrittweise Beschreibung der angewandten Strategie, von der Ermittlung der entsprechenden Werte bis zur Anwendung der entsprechenden Formel. Diese praktischen Beispiele werden dir helfen, solide Fähigkeiten in der Flächenberechnung zu entwickeln und die Bedeutung dieser Größen in realen Kontexten zu verstehen.
Komm mit auf diese lehrreiche Reise, auf der du deine Kenntnisse in der Flächenberechnung vertiefen und die nötige Sicherheit gewinnen wirst, um geometrische Probleme erfolgreich zu lösen.
Bestimme die Diagonale, den Umfang und den Flächeninhalt des Quadrats:
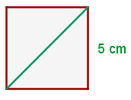
1 Wir berechnen die Diagonale mithilfe des Satzes des Pythagoras
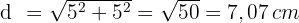
2 Wir berechnen den Umfang
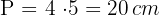
3 Wir berechnen die Fläche
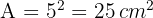
Berechne die Diagonale, den Umfang und die Fläche des Rechtecks:
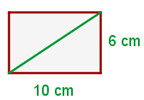
1 Wir berechnen die Diagonale mithilfe des Satzes des Pythagoras
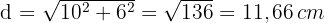
2 Wir berechnen den Umfang
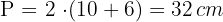
3 Wir berechnen die Fläche
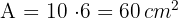
Berechne den Umfang und die Fläche der folgenden geometrischen Figur:
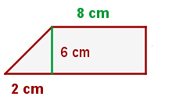
1 Wir berechnen die fehlende Seite der dreieckigen Figur mit Hilfe des Satzes des Pythagoras

2 Wir berechnen den Umfang, indem wir die Seiten der Figur addieren

3 Wir berechnen die Fläche

Berechne den Umfang und die Fläche des gleichschenkligen Trapezes:
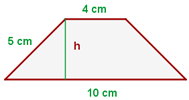
1 Wir berechnen die Höhe der Figur mit Hilfe des Satzes des Pythagoras

2 Wir berechnen den Umfang, indem wir die Seiten der Figur addieren

3 Wir berechnen die Fläche
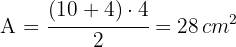
Berechne den Umfang und die Fläche des gleichseitigen Dreiecks:
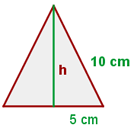
1 Wir berechnen die Höhe der Figur mithilfe des Satzes des Pythagoras

2 Wir berechnen den Umfang der Figur
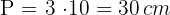
3 Wir berechnen die Fläche
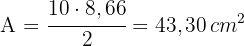
Bestimme den Umfang und die Fläche des regelmäßigen Fünfecks:
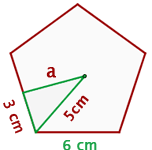
1 Wir berechnen den Wert des Apothemas mithilfe des Satzes des Pythagoras
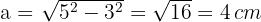
2 Wir berechnen den Umfang der Figur
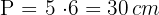
3 Wir berechnen die Fläche
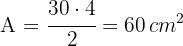
Bestimme die Fläche eines Sechsecks, das in einen Kreis mit dem Radius  cm eingeschrieben ist.
cm eingeschrieben ist.
1 Wir stellen die Figur mit den angegebenen Werten dar und stellen fest, dass wir gleichseitige Dreiecke erhalten, wenn wir Segmente vom Mittelpunkt zu den Scheitelpunkten ziehen, so dass die Seite des Sechsecks  cm beträgt
cm beträgt
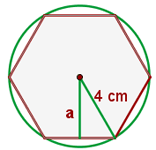
2 Wir berechnen den Wert des Apothemas mithilfe des Satzes des Pythagoras
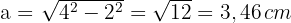
3 Wir berechnen den Umfang des Sechsecks
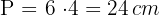
4 Wir berechnen die Fläche des Sechsecks
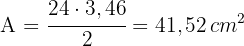
Bestimme die Fläche eines Quadrats, das in einen Kreis mit dem Radius  cm eingeschrieben ist.
cm eingeschrieben ist.
1 Wir stellen die Figur mit den angegebenen Werten dar und stellen fest, dass wir ein rechtwinkliges Dreieck erhalten, wenn wir Segmente vom Mittelpunkt zu zwei aufeinanderfolgenden Eckpunkten ziehen
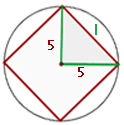
2 Wir berechnen den Wert der Seite mithilfe des Satzes des Pythagoras

3 Wir berechnen die Fläche des Quadrats
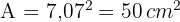
Berechne die Fläche eines gleichseitigen Dreiecks, das in einen Kreis mit dem Radius  cm eingeschrieben ist.
cm eingeschrieben ist.
1 Wir stellen die Figur mit den angegebenen Werten dar
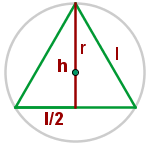
2 Der Mittelpunkt des Kreises ist das Baryzentrum. Daher
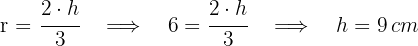
3 Wir berechnen die Seite des Dreiecks mit Hilfe des Satzes des Pythagoras

4 Wir berechnen die Fläche des Dreiecks
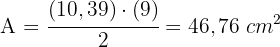
Bestimme den Flächeninhalt des Quadrats, das in einen Kreis mit dem Umfang 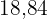 m eingeschrieben ist.
m eingeschrieben ist.
1 Wir stellen die Figur mit den gegebenen Werten dar und stellen fest, dass wir ein rechtwinkliges Dreieck mit Schenkeln, die dem Radius des Kreises entsprechen, erhalten, wenn wir Segmente vom Mittelpunkt zu zwei aufeinanderfolgenden Eckpunkten ziehen
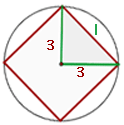
2 Wir berechnen den Radius anhand der Länge des Umfangs
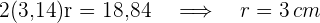
3 Die Seitenlänge des Quadrats wird mit Hilfe des Satzes des Pythagoras ermittelt
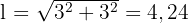
4 Wir berechnen die Fläche des Quadrats
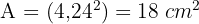
In ein Quadrat mit  cm Seitenlänge ist ein Kreis eingeschrieben, in diesen Kreis ein Quadrat und in dieses ein weiterer Kreis. Bestimme die Fläche zwischen dem letzten Quadrat und dem letzten Kreis.
cm Seitenlänge ist ein Kreis eingeschrieben, in diesen Kreis ein Quadrat und in dieses ein weiterer Kreis. Bestimme die Fläche zwischen dem letzten Quadrat und dem letzten Kreis.
1 Wir stellen die Figur mit den angegebenen Werten dar
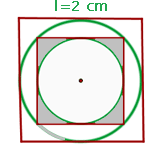
2 Der Radius des ersten Inkreises ist gleich der halben Seitenlänge des Quadrats, d.h.  . Die Diagonale des zweiten Quadrats ist gleich dem Durchmesser des ersten Kreises, d. h.
. Die Diagonale des zweiten Quadrats ist gleich dem Durchmesser des ersten Kreises, d. h.  . Wir berechnen die Seite des zweiten Quadrats mithilfe des Satzes des Pythagoras
. Wir berechnen die Seite des zweiten Quadrats mithilfe des Satzes des Pythagoras

3 Wir ermitteln die Fläche des zweiten Quadrats

4 Der Radius des zweiten Kreises ist gleich der Hälfte der Seite des zweiten Quadrats. Wir berechnen die Fläche des zweiten Kreises
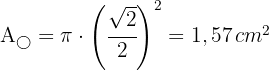
5 Die gesuchte Fläche ist

Der Umfang eines gleichschenkligen Trapezes beträgt  cm, die Grundseiten messen
cm, die Grundseiten messen  bzw.
bzw.  cm. Berechne die nicht parallelen Seiten und den Flächeninhalt.
cm. Berechne die nicht parallelen Seiten und den Flächeninhalt.
1 Wir stellen die Figur mit den angegebenen Werten dar
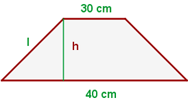
2 Berechne die nicht parallelen Seiten anhand des Umfangs
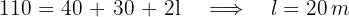
3 Wir ermitteln die Höhe mithilfe des Satzes des Pythagoras

4 Die gesuchte Fläche ist
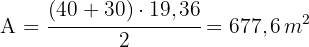
Verlängert man die nicht parallelen Seiten eines gleichschenkligen Trapezes, so entsteht ein gleichseitiges Dreieck mit einer Seitenlänge von  cm. Berechne den Flächeninhalt des Trapezes, wenn du weißt, dass das Trapez die halbe Höhe des Dreiecks hat.
cm. Berechne den Flächeninhalt des Trapezes, wenn du weißt, dass das Trapez die halbe Höhe des Dreiecks hat.
1 Aus den gegebenen Werten ergibt sich, dass die längere Grundseite  und die kürzere Grundseite
und die kürzere Grundseite 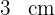 misst
misst
2 Wir berechnen die Höhe des Dreiecks mithilfe des Satzes des Pythagoras
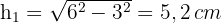
3 Wir ermitteln die Höhe des Trapezes, die die Hälfte der Höhe des Dreiecks ist

4 Die gesuchte Fläche ist
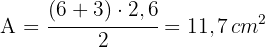
Die Fläche eines Quadrats ist  . Berechne die Fläche des regelmäßigen Sechsecks, das denselben Umfang hat.
. Berechne die Fläche des regelmäßigen Sechsecks, das denselben Umfang hat.
1 Wir berechnen den Wert der Seite des Quadrats anhand seiner Fläche
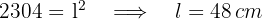
2 Berechne den Umfang des Quadrats
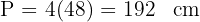
3 Der Umfang des Sechsecks beträgt  , weshalb die Seite des Sechsecks
, weshalb die Seite des Sechsecks  misst
misst
4 Wir stellen die Figur des Sechsecks mit den erhaltenen Werten dar und berechnen ihr Apothema
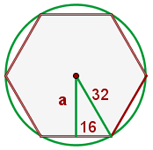
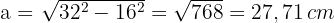
5 Wir berechnen die Fläche des Sechsecks

Ein Quadrat wird in einen Kreis mit dem Radius  cm eingeschrieben, und an den Seiten des Quadrats und nach außen hin werden gleichseitige Dreiecke konstruiert. Bestimme die Fläche des so entstandenen Sterns.
cm eingeschrieben, und an den Seiten des Quadrats und nach außen hin werden gleichseitige Dreiecke konstruiert. Bestimme die Fläche des so entstandenen Sterns.
1 Wir stellen die Figur mit den gegebenen Werten dar
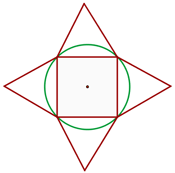
2 Wir berechnen die Seite des Quadrats und stellen fest, dass die Diagonale gleich dem Durchmesser des Umfangs ist

3 Die Höhe eines gleichseitigen Dreiecks lässt sich mithilfe des Satzes des Pythagoras bestimmen
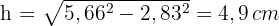
4 Die Fläche eines Dreiecks ist
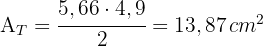
5 Die Fläche des Quadrats ist
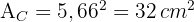
6 Die Fläche des Sterns ist
In ein regelmäßiges Sechseck mit einer Seitenlänge von  cm wird ein Kreis eingeschrieben und außerdem wird das Sechseck von einem Kreis umschrieben. Berechne die Fläche der kreisförmigen Krone, die so entsteht.
cm wird ein Kreis eingeschrieben und außerdem wird das Sechseck von einem Kreis umschrieben. Berechne die Fläche der kreisförmigen Krone, die so entsteht.
1 Wir stellen die Figur mit den gegebenen Werten dar
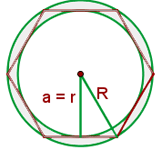
2 Der Radius des umschriebenen Kreises ist gleich der Seite des Sechsecks, d. h. 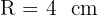 . Der Radius des Inkreises ist gleich dem Apothema, das wir mit dem Satz des Pythagoras berechnen.
. Der Radius des Inkreises ist gleich dem Apothema, das wir mit dem Satz des Pythagoras berechnen.
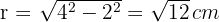
3 Die Fläche der Krone ist gleich der Differenz der Flächen der Kreise
Eine Sehne eines Kreises misst  cm und befindet sich
cm und befindet sich  cm vom Mittelpunkt entfernt. Berechne die Fläche des Kreises.
cm vom Mittelpunkt entfernt. Berechne die Fläche des Kreises.
1 Wir stellen die Figur mit den gegebenen Werten dar
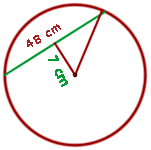
2 Der Radius des Kreises ergibt sich aus dem Satz des Pythagoras

3 Die Fläche des Kreises ist
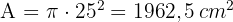
Die Schenkel eines rechtwinkligen Dreiecks, das in einen Kreis eingeschrieben ist, messen 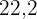 cm und
cm und 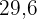 cm. Berechne den Umfang und die Fläche des Kreises.
cm. Berechne den Umfang und die Fläche des Kreises.
1 Wir stellen die Figur mit den gegebenen Werten dar
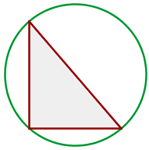
2 Die Hypotenuse des Dreiecks ist gleich dem Durchmesser des Umfangs. Wir berechnen sie mithilfe des Satzes des Pythagoras.
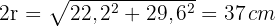
3 Der Umfang des Kreises ist
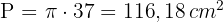
4Die Fläche des Kreises ist
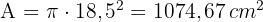
Berechne den Flächeninhalt der kreisförmigen Krone, die durch die In- und Umkreise eines Quadrats, dessen Diagonale  m misst, bestimmt wird.
m misst, bestimmt wird.
1 Wir stellen die Figur mit den gegebenen Werten dar
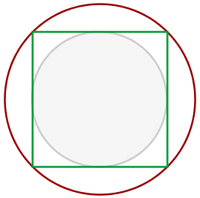
2 Der Radius des umschriebenen Kreises entspricht der halben Diagonale des Quadrats, d. h.  . Der Radius des Inkreises ist gleich der halben Seite des Quadrats, die wir mithilfe des Satzes des Pythagoras berechnen
. Der Radius des Inkreises ist gleich der halben Seite des Quadrats, die wir mithilfe des Satzes des Pythagoras berechnen
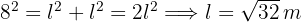
3 Die Fläche der Krone ist gleich der Differenz der Flächen der Kreise

Auf einem Kreis mit dem Radius  cm soll ein Mittelpunktswinkel von
cm soll ein Mittelpunktswinkel von 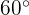 eingezeichnet werden. Berechne die Fläche des Kreissegments, das sich zwischen der Sehne, die die beiden äußersten Punkte der Radien und den entsprechenden Bogen verbindet, befindet.
eingezeichnet werden. Berechne die Fläche des Kreissegments, das sich zwischen der Sehne, die die beiden äußersten Punkte der Radien und den entsprechenden Bogen verbindet, befindet.
1 Wir stellen die Figur mit den gegebenen Werten dar
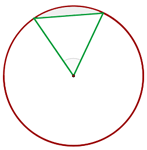
2 Wir berechnen die Fläche des Segments
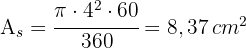
3 Das entstandene Dreieck ist gleichseitig und wir berechnen seine Höhe mithilfe des Satzes des Pythagoras
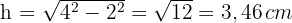
4 Wir berechnen die Fläche des Dreiecks

5 Die gesuchte Fläche ist gleich der Differenz der Flächen
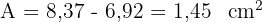
Bei einem gleichseitigen Dreieck mit der Seitenlänge  m ist die Fläche eines der Segmente zu bestimmen, die durch den umschriebenen Kreis und die Radien, die durch die Eckpunkte gehen, bestimmt werden.
m ist die Fläche eines der Segmente zu bestimmen, die durch den umschriebenen Kreis und die Radien, die durch die Eckpunkte gehen, bestimmt werden.
1 Wir stellen die Figur mit den gegebenen Werten dar
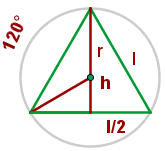
2 Wir berechnen die Höhe des gleichseitigen Dreiecks mithilfe des Satzes des Pythagoras
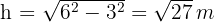
3 Der Mittelpunkt des Kreises ist das Baryzentrum. Deshalb:
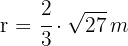
4 Wir berechnen die Fläche des Segments von 
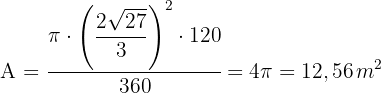
Berechne die Fläche eines konvexen Vierecks 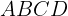 mit dem Umfang
mit dem Umfang 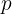 und dem Inkreis
und dem Inkreis 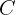 mit dem Radius
mit dem Radius  .
.
1 Wir stellen die Figur mit den gegebenen Werten dar
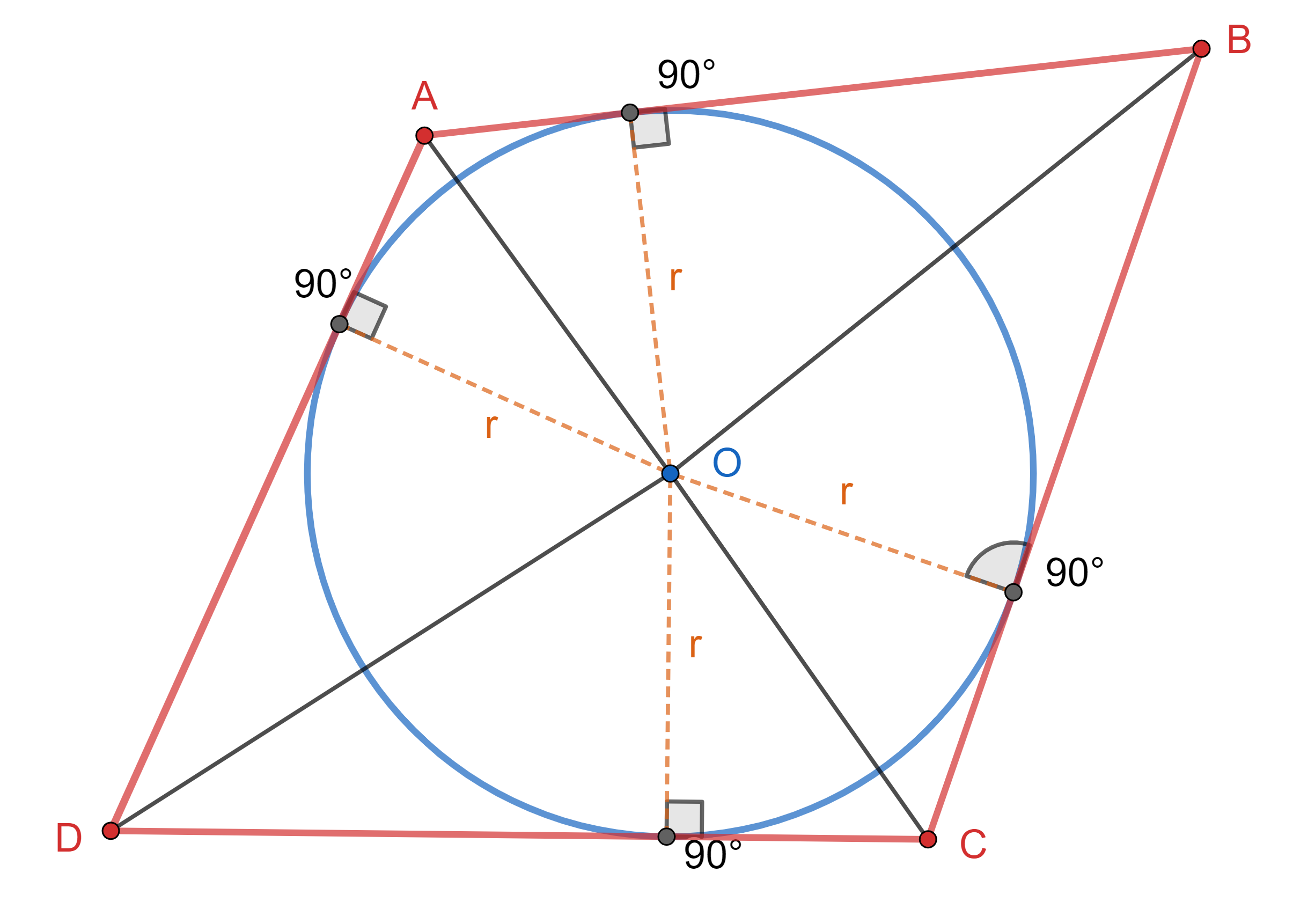
2
Nun stellen wir fest, dass die Fläche des Vierecks in 4 Dreiecke mit einem gemeinsamen Scheitelpunkt im Mittelpunkt des Kreises aufgeteilt werden kann. Jedes dieser Dreiecke hat eine Fläche, die gleich der Hälfte seiner Höhe (in diesem Fall der Radius) mal seiner Grundseite (in diesem Fall entsprechend den Seiten des Vierecks) ist. Wir haben also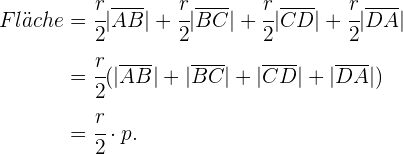
Löse folgende Problemstellungen.
1 Berechne die Fläche eines konvexen Vierecks 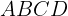 mit dem Umfang
mit dem Umfang 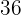 und dem Inkreis
und dem Inkreis 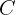 mit dem Radius
mit dem Radius 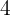 .
.
2 Berechne die Fläche eines konvexen Vierecks 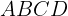 mit dem Umfang
mit dem Umfang  und dem Inkreis
und dem Inkreis 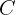 mit dem Radius
mit dem Radius 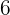 .
.
1
Wenn wir uns Aufgabe 22 ansehen, stellen wir fest, dass die Fläche mithilfe von 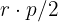 berechnet wird, wobei
berechnet wird, wobei 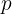 der Umfang und
der Umfang und  der Radius des Kreises ist. Entonces,
der Radius des Kreises ist. Entonces, 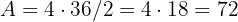 .
.
2 Wenn wir die Formel direkt anwenden, erhalten wir 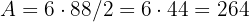 .
.
Berechne die Fläche eines konvexen Vierecks mit den Seiten  .
.
1 Wir stellen grafisch dar
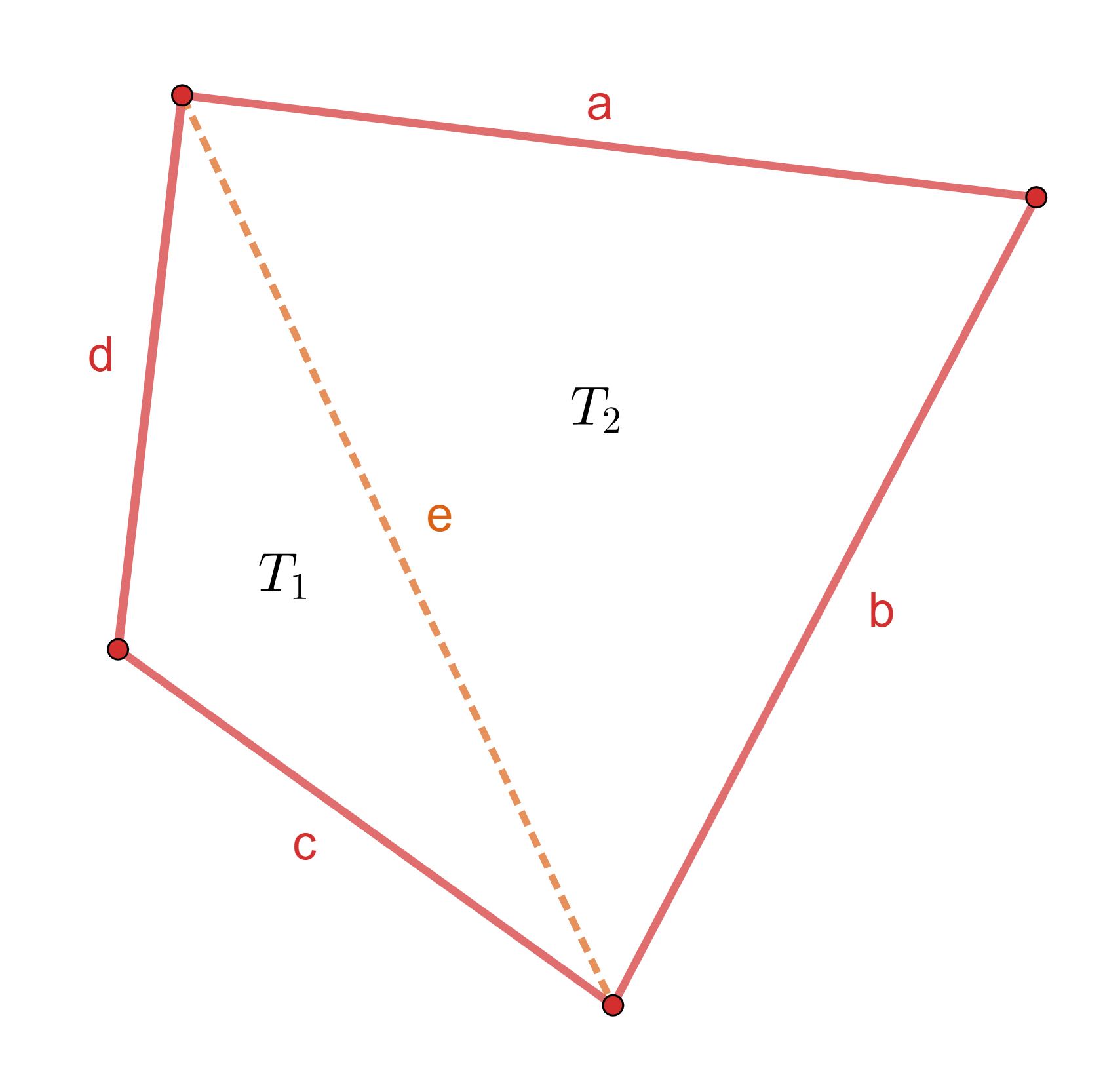
2 Wir sehen nun, dass sich die Gesamtfläche in 2 Dreiecke 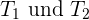 teilen lässt. Wir können für jedes der Dreiecke den Satz des Heron anwenden. Der halbe Umfang ist
teilen lässt. Wir können für jedes der Dreiecke den Satz des Heron anwenden. Der halbe Umfang ist

Die Flächen sind also

und daher ergibt ihre Summe die Fläche des Vierecks:
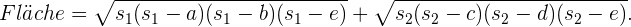
Berechne die Fläche der folgenden geometrischen Figur:
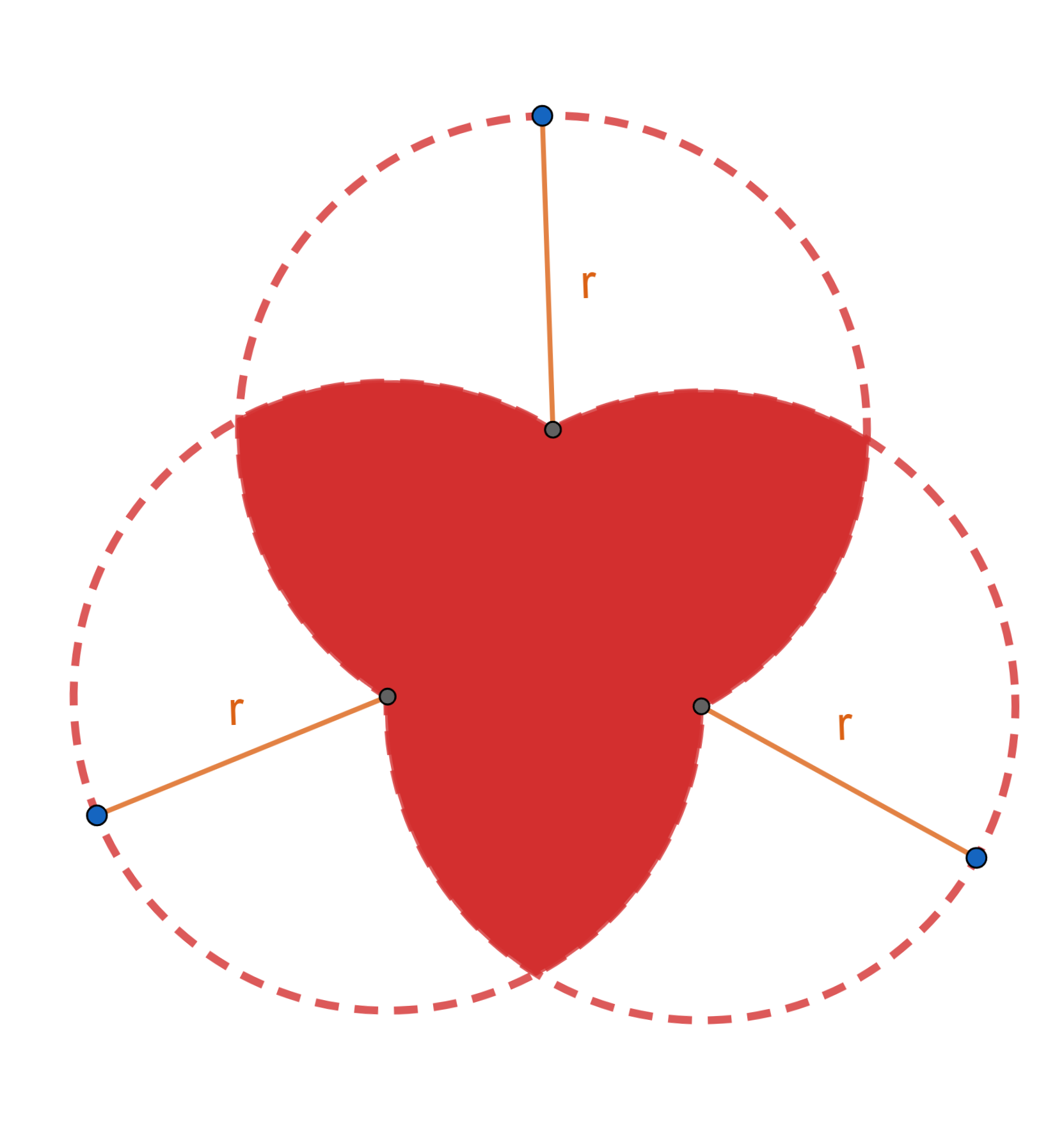
1 Wir zeichnen weitere Linien ein, um die Figur zu vereinfachen:
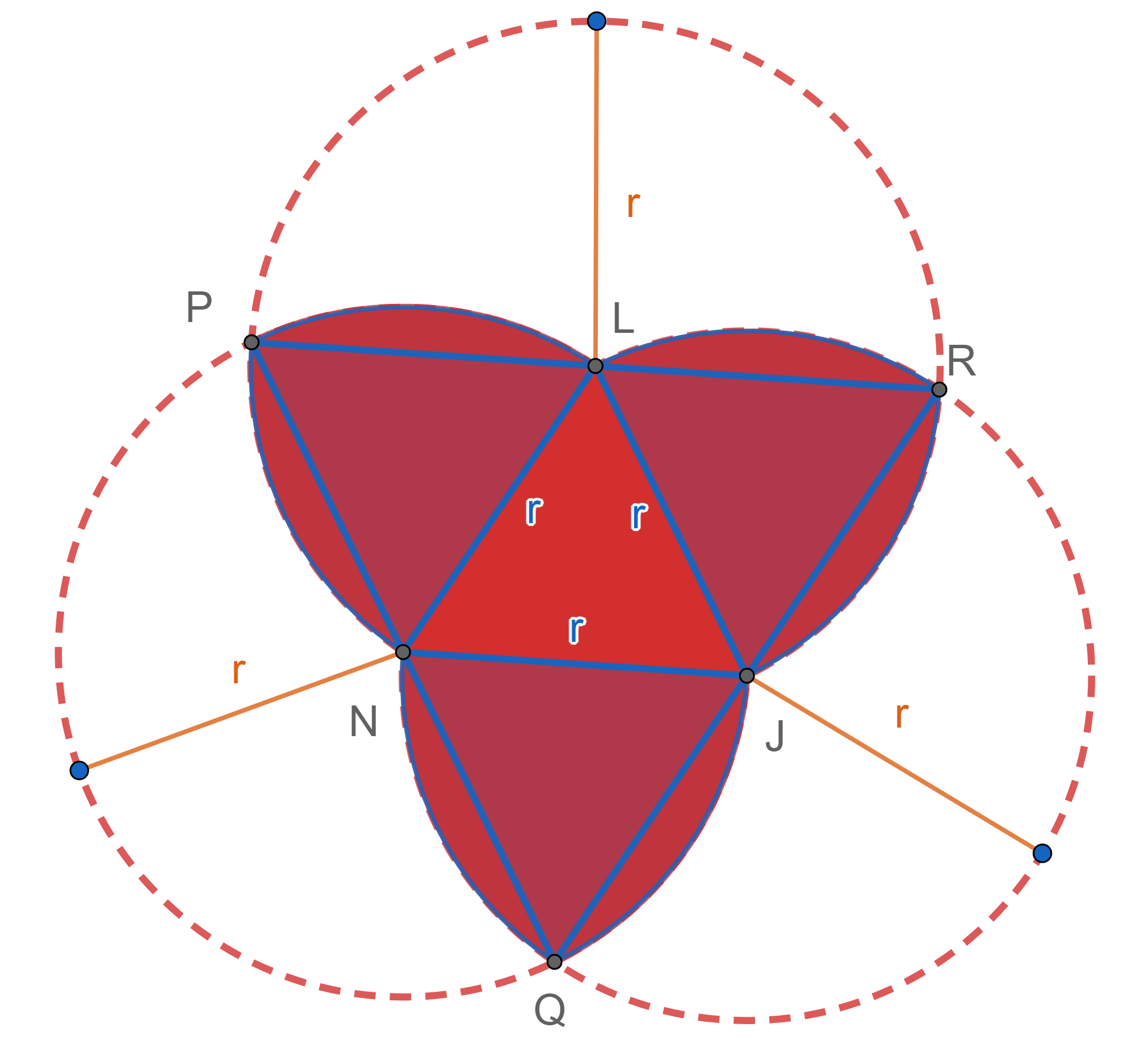
2 Wir können den Bereich in 2 Arten von Teilen aufteilen: en ein gleichseitiges Dreieck, dessen Seitenlänge dem Durchmesser eines Kreises entspricht, das heißt 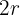 und sechs kreisförmige Segmente. Die Fläche des Dreiecks ist
und sechs kreisförmige Segmente. Die Fläche des Dreiecks ist
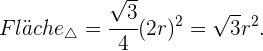
Nun haben die kreisförmigen Segmente eine Fläche, die vom Winkel abhängt. In diesem Fall sind die Winkel alle gleich und entsprechen dem eines gleichseitigen Dreiecks mit einem Bogenmaß von  . Somit sind die Flächen
. Somit sind die Flächen
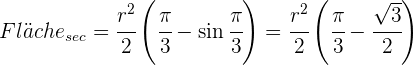
Dann multiplizieren wir dies mit 6, um die Summe aller 6 Segmente zu erhalten, und am Ende addieren wir die Fläche des Dreiecks, um die Gesamtfläche der geometrischen Figur zu erhalten:
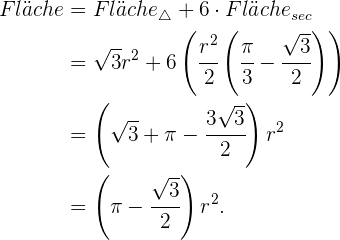
Mit KI zusammenfassen:


