Kapitel
- Satz des Pythagoras
- Kathetensatz
- Höhensatz
- Diagonale des Quadrats
- Diagonale des Rechtecks
- Schräge Seite des rechtwinkligen Trapezes
- Höhe des gleichschenkligen Trapezes
- Höhe des gleichseitigen Dreiecks
- Apothema eines regelmäßigen Vielecks
- Seite eines eingeschriebenen gleichseitigen Dreiecks
- Seite eines eingeschriebenen Quadrats
Im Folgenden werden wir verschiedene Formeln im Zusammenhang mit rechtwinkligen Dreiecken betrachten, von denen viele aus dem bekannten Satz des Pythagoras abgeleitet sind. Daher wird dieser Satz als Erstes behandelt.

Satz des Pythagoras
"In jedem rechtwinkligen Dreieck ist das Quadrat der Hypotenuse gleich der Summe der Quadrate der Katheten."
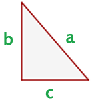
Aus der obigen Aussage ergibt sich folgende Formel ,
,
aus der wir die Länge jeder Seite eines rechtwinkligen Dreiecks berechnen können
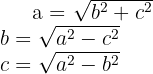
Kathetensatz
"In einem rechtwinkligen Dreieck ist das Quadrat einer der Katheten gleich dem Produkt ihrer Abbildung auf die Hypotenuse und der Hypotenuse selbst."
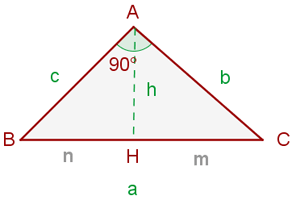
Wir stellen die obige Aussage mit den folgenden Gleichungen dar
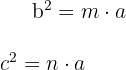
Höhensatz
"In einem rechtwinkligen Dreieck ist das Quadrat der Höhe, gemessen an der Hypotenuse, gleich dem Produkt der Abbildungen der beiden Katheten auf die Hypotenuse."
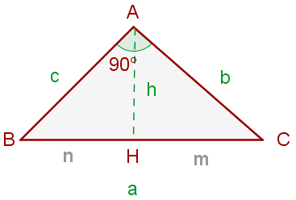
Daraus können wir folgende Formel ableiten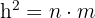
Diagonale des Quadrats
Zu beachten ist, dass die Diagonale des Quadrats die Hypotenuse eines rechtwinkligen Dreiecks mit zwei gleichen Katheten ist.
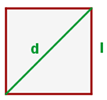
somit lautet die Gleichung der Diagonalen
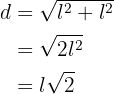
Diagonale des Rechtecks
Ähnlich wie im vorherigen Fall ist die Diagonale des Rechtecks die Hypotenuse eines rechtwinkligen Dreiecks, dessen Katheten die Seiten des Rechtecks sind.
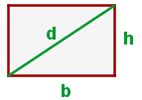
somit lautet die Gleichung der Diagonalen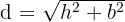
Schräge Seite des rechtwinkligen Trapezes
Bei einem rechtwinkligen Trapez bildet eine der Seiten ein rechtwinkliges Dreieck
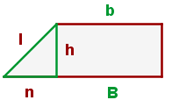
wobei die Hypotenuse die schräge Seite ist, eine Kathete die Höhe und die andere die Differenz zwischen den Grundseiten. Daher wird ihre schräge Seite mithilfe des Satzes des Pythagoras berechnet.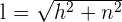 ,
,
wobei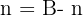
Höhe des gleichschenkligen Trapezes
Um die Höhe eines gleichschenkligen Trapezes zu berechnen, verwenden wir ein rechtwinkliges Dreieck, bei dem die Hypotenuse die schräge Seite ist, eine Kathete die Höhe und die andere Kathete die Differenz zwischen  und
und  ist
ist
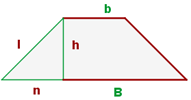
somit ist 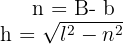
Höhe des gleichseitigen Dreiecks
Die Höhe eines gleichseitigen Dreiecks kann auch anhand des Satzes des Pythagoras berechnet werden
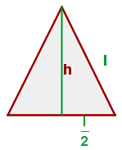
die Seiten  ,
,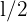 sind die Katheten und
sind die Katheten und  die Hypotenuse. Also
die Hypotenuse. Also
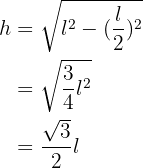
Apothema eines regelmäßigen Vielecks
Wir können das Apothema eines regelmäßigen Vielecks berechnen, wenn wir seine Seitenlänge und seinen Radius kennen.
Anhand des Satzes des Pythagoras ergibt sich für das Apothema die Formel
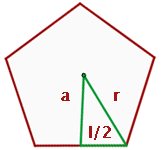
Seite eines eingeschriebenen gleichseitigen Dreiecks
Um die Seite des eingeschriebenen Dreiecks zu berechnen, konstruieren wir ein kleines zusätzliches gleichseitiges Dreieck wie in der Abbildung
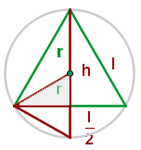
daraus folgt, dass
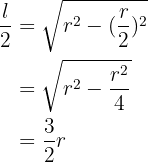
und somit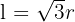
Seite eines eingeschriebenen Quadrats
Wir stellen fest, dass
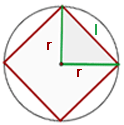
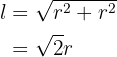
Mit KI zusammenfassen:












