Kapitel
Ein gleichseitiges Dreieck hat drei gleiche Seiten und Winkel.
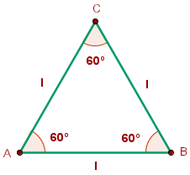

Umfang eines gleichseitigen Dreiecks
Der Umfang eines Dreiecks ist gleich der Summe seiner drei Seiten. Für ein gleichseitiges Dreieck, dessen drei Seiten gleich sind, gilt

Beispiel: Berechne den Umfang eines gleichseitigen Dreiecks mit  Seitenlänge.
Seitenlänge.
Durch Anwendung der Umfangsformel erhältst du
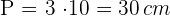
Höhe eines gleichseitigen Dreiecks
Unter Anwendung des Satzes von Pythagoras kannst du die Höhe berechnen:

Durch Berechnung der Wurzeln erhältst du

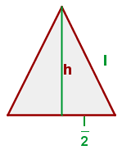
Beispiel: Berechne die Höhe eines gleichseitigen Dreiecks mit  Seitenlänge.
Seitenlänge.
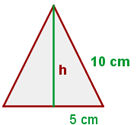
Bei Anwendung der Höhenformel erhältst du
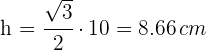
Flächeninhalt eines gleichseitigen Dreiecks
Der Flächeninhalt eines Dreiecks ist gleich der Hälfte des Produkts aus seiner Grundseite und seiner Höhe. Für ein gleichseitiges Dreieck gilt
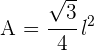
Beispiel: Berechne den Flächeninhalt eines gleichseitigen Dreiecks mit  Seitenlänge.
Seitenlänge.
Wende die Formel für den Flächeninhalt eines Dreiecks an
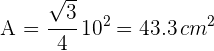
Beispiel: Der Umfang eines gleichseitigen Dreiecks beträgt 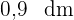 und die Höhe beträgt
und die Höhe beträgt 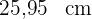 . Berechne die Fläche des Dreiecks.
. Berechne die Fläche des Dreiecks.
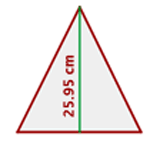
Da das Dreieck gleichseitig ist, sind seine drei Seiten gleich, also 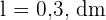
Da ein Dezimeter hundert Zentimetern entspricht, ist 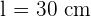
Wende die Formel für den Flächeninhalt eines Dreiecks an
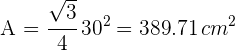
Apothema des gleichseitigen Dreiecks
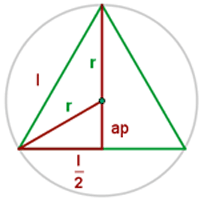
Die Seite eines eingeschriebenen gleichseitigen Dreiecks ist:
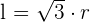
Eliminiere den Radius
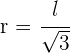
Wende den Satz des Pythagoras an
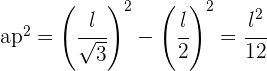
Die Berechnung der Quadratwurzel ergibt

Beispiel: Berechne das Apothema eines gleichseitigen Dreiecks mit 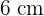 Seitenlänge.
Seitenlänge.
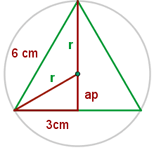
Unter Anwendung der Formel des Apothemas erhältst du
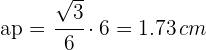
Eigenschaften des gleichseitigen Dreiecks
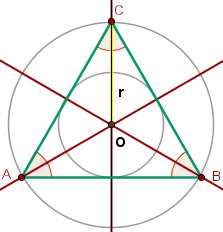
In einem gleichseitigen Dreieck fallen das Orthozentrum, der Schwerpunkt, der Umkreismittelpunkt und der Inkreismittelpunkt zusammen.
Der Mittelpunkt des Kreises ist der Schwerpunkt und die Höhe fällt mit dem Median zusammen, so dass der Radius des umschriebenen Kreises gleich zwei Drittel der Höhe ist.

Übungen
Berechne den Flächeninhalt eines gleichseitigen Dreiecks, das in einen Kreis mit dem Radius 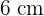 eingeschrieben ist.
eingeschrieben ist.
1 Stelle das Problem grafisch dar
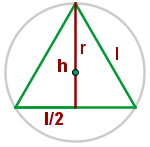
2 Der Mittelpunkt des Kreises ist der Schwerpunkt, also ist 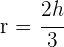 und du erhältst
und du erhältst

3 Um den Flächeninhalt des Dreiecks zu ermitteln, musst du seine Grundseite kennen. Teile dazu das gleichseitige Dreieck in zwei rechtwinklige Dreiecke und wende den Satz des Pythagoras an
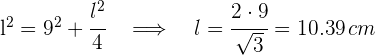
4 Um seine Fläche zu berechnen, verwendest du
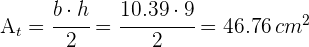
Gebe ein gleichseitiges Dreieck mit 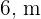 Seiten an und finde die Fläche eines der Sektoren, die durch den Umkreis und die Radien durch die Scheitelpunkte bestimmt werden.
Seiten an und finde die Fläche eines der Sektoren, die durch den Umkreis und die Radien durch die Scheitelpunkte bestimmt werden.
1 Stelle das Problem grafisch dar
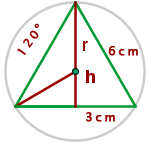
2 Der Mittelpunkt des Kreises ist der Schwerpunkt, also 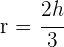
3 Um die Höhe des Dreiecks zu ermitteln, wendest du den Satz des Pythagoras an

4 Berechne den Radius
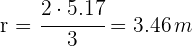
5 Die Fläche eines der Sektoren, die durch den umschriebenen Umfang und durch die Scheitelpunkte gehenden Radien bestimmt wird, ist

Berechne die Seite eines gleichseitigen Dreiecks, das in einen Kreis mit dem Radius  eingeschrieben ist.
eingeschrieben ist.
1 Stelle das Problem grafisch dar
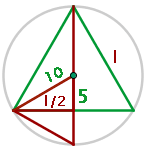
2 Betrachte das rechtwinklige Dreieck mit der Seite  , der Hypotenuse
, der Hypotenuse  und der Restseite
und der Restseite  . Wende den Satz des Pythagoras an
. Wende den Satz des Pythagoras an
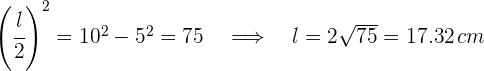
Mit KI zusammenfassen:













