Löse die folgenden Probleme:
1Die Hypotenuse eines rechtwinkligen Dreiecks,  , misst
, misst  und die Abbildung ihrer Kathete
und die Abbildung ihrer Kathete  auf sie misst
auf sie misst 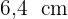 .
.
Wie lang ist die Kathete  ?
?  .
.
Dieses Feld ist erforderlich.
Wir wenden den Kathetensatz an:
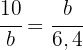
Wir bestimmen 

Die Kathete  misst
misst  .
.
Wie lang ist die Kathete  ?
? 
Dieses Feld ist erforderlich.
Wir wenden den Satz des Pythagoras an

Die Kathete  misst
misst  .
.
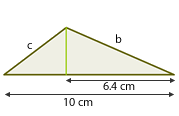
2Die Abbildungen der Katheten  und
und  eines rechtwinkligen Dreiecks messen
eines rechtwinkligen Dreiecks messen  und
und 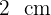 .
.
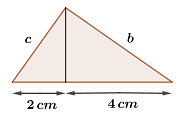
Wie lang ist die Kathete  ? Runde auf eine Dezimalstelle.
? Runde auf eine Dezimalstelle. 
Dieses Feld ist erforderlich.
Wir wenden den Kathetensatz an:
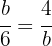
Wir bestimmen 
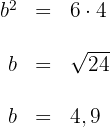
Die Kathete  misst
misst 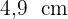 .
.
Wie lang ist die Kathete  ?
? 
Dieses Feld ist erforderlich.
Wir wenden erneut den Kathetensatz an
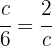
Wir bestimmen 
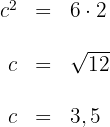
Die Kathete  misst
misst 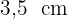 .
.
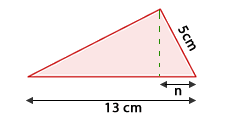
3Die Abbildung der Kathete  eines rechtwinkligen Dreiecks misst
eines rechtwinkligen Dreiecks misst  und seine Höhe
und seine Höhe 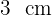 .
.
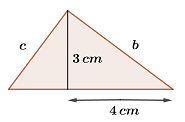
Wie lang ist die Kathete  ? Runde auf eine Dezimalstelle.
? Runde auf eine Dezimalstelle. 
Dieses Feld ist erforderlich.
Wir wenden den Satz des Pythagoras an:
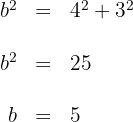
Die Kathete  misst
misst  .
.
Wie lang ist die Kathete  ?
? 
Dieses Feld ist erforderlich.
Wir wenden den Kathetensatz an
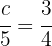
Wir bestimmen 
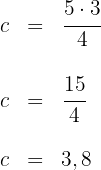
Die Kathete  misst
misst 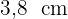 .
.
4Die Kathete  eines rechtwinkligen Dreiecks misst
eines rechtwinkligen Dreiecks misst  und die Kathete
und die Kathete  misst
misst  .
.
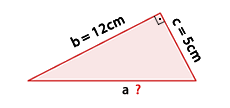
Wie lang ist die Hypotenuse  dieses Dreiecks?
dieses Dreiecks? 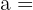
 .
.
Dieses Feld ist erforderlich.
Wir wenden den Satz des Pythagoras an

Die Hypotenuse  misst
misst  .
.
Gib die Länge der Abbildungen der Katheten  und
und  an, gerundet auf zwei Dezimalstellen.
an, gerundet auf zwei Dezimalstellen.
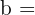
 .
.

 .
.
Dieses Feld ist erforderlich.
Wir wenden den Kathetensatz an, um die Maße der Abbildungen zu berechnen:
 Wir bestimmen
Wir bestimmen 
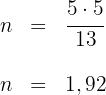
Die Abbildung der Kathete  misst
misst 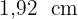 .
.
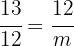 Wir bestimmen
Wir bestimmen 
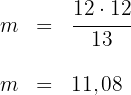
Die Abbildung der Kathete  misst
misst 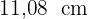 .
.
Wie hoch ist die Höhe dieses Dreiecks? 
 .
.
Dieses Feld ist erforderlich.
Um die Höhe zu berechnen, wenden wir den Satz des Pythagoras auf eines der beiden Dreiecke an, die wir in der Abbildung sehen können. Wir nehmen zum Beispiel das kleinere Dreieck: 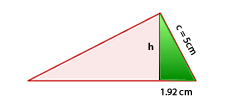
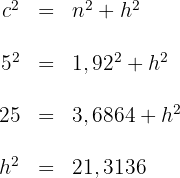
Die Höhe  misst
misst 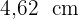 .
.
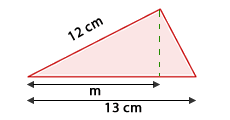
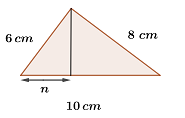
5Die Kathete  eines rechwinkligen Dreiecks misst
eines rechwinkligen Dreiecks misst  und seine Hypotenuse
und seine Hypotenuse  misst
misst  .
.
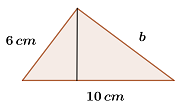
Wie lang ist die Kathete  dieses Dreiecks?
dieses Dreiecks? 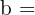
 .
.
Dieses Feld ist erforderlich.
Wir wenden den Satz des Pythagoras an
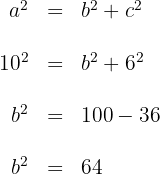
Die Kathete  misst
misst  .
.
Gib die Länge der Abbildungen der Katheten  und
und  an, gerundet auf zwei Dezimalstellen.
an, gerundet auf zwei Dezimalstellen.
 .
.

 .
.
Dieses Feld ist erforderlich.
Wir wenden den Kathetensatz an, um die Länge der Abbildungen zu erhalten:
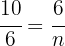 Wir bestimmen
Wir bestimmen 
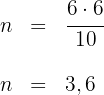
Die Abbildung der Kathete  misst
misst 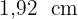 .
.
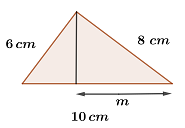
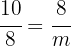 Wir bestimmen
Wir bestimmen 
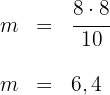
Die Abbildung der Kathete  misst
misst 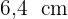 .
.
Wie hoch ist die Höhe dieses Dreiecks? 
 .
.
Dieses Feld ist erforderlich.
Um die Höhe zu berechnen, wenden wir einfach den Satz des Pythagoras auf eines der beiden Dreiecke an, die wir in der Abbildung sehen können. Nehmen wir zum Beispiel das kleinere Dreieck:
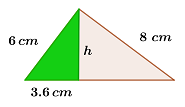
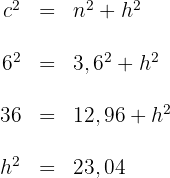
Die Höhe  misst
misst 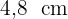 .
.
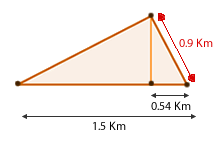
6Die Häuser von vier Freunden sind wie in der folgenden Abbildung dargestellt angeordnet. Da wir wissen, dass die Entfernung zwischen Beas und Karls Haus 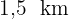 beträgt und die Entfernung zwischen dem Haus von Bea und dem Haus von David
beträgt und die Entfernung zwischen dem Haus von Bea und dem Haus von David 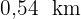 , können wir die fehlenden Entfernungen berechnen:
, können wir die fehlenden Entfernungen berechnen:
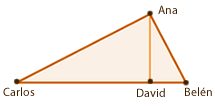
Entfernung zwischen Beas und Annas Haus 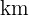 .
.
Dieses Feld ist erforderlich.
Zunächst einmal sehen wir, dass es sich um ein rechtwinkliges Dreieck handelt, sodass wir bei Bedarf den Kathetensatz anwenden können.
Entfernung zwischen Beas und Annas Haus 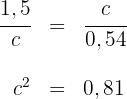
Die gesuchte Entfernung ist 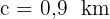 .
.
Entfernung zwischen Davids und Karls Haus 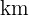 .
.
Dieses Feld ist erforderlich.
Entfernung zwischen Davids und Karls Haus
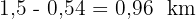 .
.
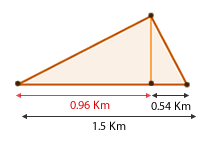
Entfernung zwischen Annas und Davids Haus  .
.
Dieses Feld ist erforderlich.
Entfernung zwischen Annas und Davids Haus. Wir wenden den Satz des Pythagoras an: 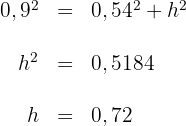
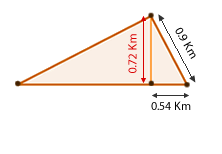
7 Drei Schiffe nähern sich einem Leuchtturm, wie in der Abbildung dargestellt, und bilden dabei rechtwinklige Dreiecke. Da die Entfernung vom Leuchtturm zum Schiff 1 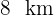 und die Entfernung vom Leuchtturm zum Schiff 3
und die Entfernung vom Leuchtturm zum Schiff 3 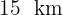 beträgt, können wir folgende Entfernung berechnen:
beträgt, können wir folgende Entfernung berechnen:
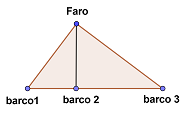
Entfernung zwischen Schiff 1 und Schiff 2  .
.
Dieses Feld ist erforderlich.
Wir wenden den Satz des Pythagoras an, um die Entfernung zwischen Schiff 1 und 3 zu erhalten 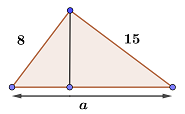
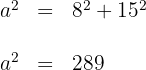
Die gesuchte Entfernung ist 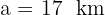 .
.
Entfernung zwischen Schiff 1 und Schiff 3  .
.
Dieses Feld ist erforderlich.
Entfernung von Schiff 2 zu Schiff 3
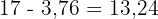
Mit KI zusammenfassen:


