Wähle die korrekte Option:
Zwei aufeinanderfolgende Quadranten bilden einen Mittelpunktswinkel von...
Bitte wähle eine Antwort aus.
Das Maß des Bogens, der durch das Zeichnen des obigen Winkels definiert wird, ist...
Bitte wähle eine Antwort aus.
Ein eingeschriebener Winkel, der einen Bogen von  aufspannt, misst...
aufspannt, misst...
Bitte wähle eine Antwort aus.
Ein eingeschriebener Winkel von 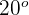 beschreibt einen Bogen von...
beschreibt einen Bogen von...
Bitte wähle eine Antwort aus.
Die Seiten und die Verlängerungen eines Innenwinkels bilden einen Bogen von 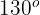 und einen weiteren von
und einen weiteren von  , also misst dieser Winkel...
, also misst dieser Winkel...
Bitte wähle eine Antwort aus.
Die Differenz zwischen den Maßen der Bögen, die die Seiten eines Winkels um den Umfang aufspannen, ist 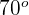 , also ist das Maß des Winkels...
, also ist das Maß des Winkels...
Bitte wähle eine Antwort aus.
Einer der Bögen, die die Seiten eines Außenwinkels um den Kreis aufspannen, misst 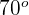 , also ist das Maß des Winkels...
, also ist das Maß des Winkels...
Bitte wähle eine Antwort aus.
Der kleinere Bogen, der einen Außenwinkel auf dem Kreis beschreibt, ist 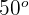 und das Maß dieses Winkels ist
und das Maß dieses Winkels ist  . Dann ist das Maß des anderen Bogens, der diesen Winkel beschreibt,...
. Dann ist das Maß des anderen Bogens, der diesen Winkel beschreibt,...
Bitte wähle eine Antwort aus.
Wenn  der Wert des gesuchten Bogens ist (es handelt sich um einen Außenwinkel), haben wir:
der Wert des gesuchten Bogens ist (es handelt sich um einen Außenwinkel), haben wir:
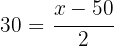
Wir bestimmen  und erhalten
und erhalten 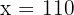
Wenn ein halb einbeschriebener Winkel 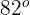 misst, misst der Bogen, den er beschreibt...
misst, misst der Bogen, den er beschreibt...
Bitte wähle eine Antwort aus.
Ein Innenwinkel misst 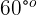 und einer der von ihm bestimmten Bögen ist
und einer der von ihm bestimmten Bögen ist 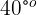 . Der andere Bogen misst also...
. Der andere Bogen misst also...
Bitte wähle eine Antwort aus.
Wenn  der Wert des gesuchten Bogens ist (es handelt sich um einen Innenwinkel), haben wir:
der Wert des gesuchten Bogens ist (es handelt sich um einen Innenwinkel), haben wir:

Damit der zweite Teil der Gleichung gleich  ist, muss man prüfen, ob der Ausdruck in Klammern gleich
ist, muss man prüfen, ob der Ausdruck in Klammern gleich  ist. Somit erhalten wir
ist. Somit erhalten wir 
Beanworte die folgenden Fragestellungen:
Wenn wir einen Kreis in 5 gleiche Bögen unterteilen, wie lang ist jeder dieser Bögen?

Und jeder der Mittelpunktswinkel, die diesen Bögen entsprechen?

Dieses Feld ist erforderlich.
Da der gesamte Kreis  beträgt, kann man den Umfang in 5 gleiche Bögen aufteilen, von denen jeder folgendes Maß hat
beträgt, kann man den Umfang in 5 gleiche Bögen aufteilen, von denen jeder folgendes Maß hat
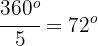
Die Mittelpunktswinkel, die diesen Bögen entsprechen, haben die gleiche Größe wie die Bögen, d. h.  .
.
Wenn wir den Kreis in gleiche Teile unterteilen und der Mittelpunktswinkel jedes Teils 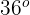 ist, in wie viele Teile wurde der Kreis dann unterteilt?
ist, in wie viele Teile wurde der Kreis dann unterteilt?

Dieses Feld ist erforderlich.
Wir wissen, dass der volle Kreisumfang  beträgt.
beträgt.
Dividiert man  durch
durch 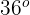 , erhält man die Teile, in die der Umfang unterteilt wurde.
, erhält man die Teile, in die der Umfang unterteilt wurde.
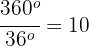 gleiche Teile.
gleiche Teile.
Gib die Maße der fehlenden Winkel an.


Dieses Feld ist erforderlich.
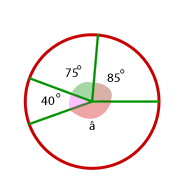
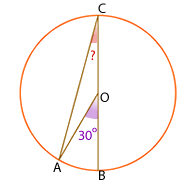
Bei dem ersten Kreis möchten wir den fehlenden Winkel berechnen:

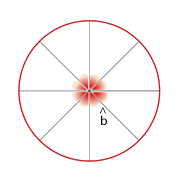
Beim zweiten Umfang wollen wir jeden der gleichen Winkel berechnen, in die der Kreis geteilt ist, es gibt also 8 gleiche Teile:

Berechne den Wert des fehlenden Winkels in jedem der folgenden Kreise


Dieses Feld ist erforderlich.
Orangefarbener Kreis
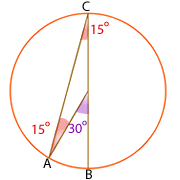
Der Winkel 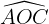 ist der Supplementwinkel zu
ist der Supplementwinkel zu  und misst somit
und misst somit 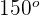 .
.
Das Dreieck 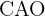 ist gleichschenklig, weil es zwei gleiche Seiten hat (die Radien). Daher sind auch die beiden anderen Winkel gleich und messen
ist gleichschenklig, weil es zwei gleiche Seiten hat (die Radien). Daher sind auch die beiden anderen Winkel gleich und messen  .
.
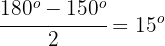
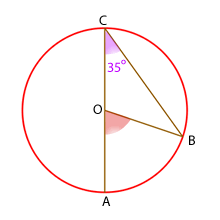
Roter Kreis
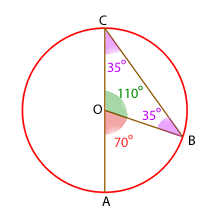
Der Winkel  misst
misst 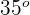 , da das Dreieck
, da das Dreieck 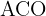 gleichschenklig ist. Zwei der Seiten sind also die Radien (und somit gleich).
gleichschenklig ist. Zwei der Seiten sind also die Radien (und somit gleich).
Da die Seiten eines Dreiecks die Summe von  ergeben müssen, messen die Winkel des Dreiecks
ergeben müssen, messen die Winkel des Dreiecks 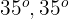 und
und  .
.
Der Winkel  misst
misst 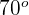 , weil er der Supplementwinkel zu
, weil er der Supplementwinkel zu 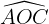 ist
ist
In beiden Fällen ist der Mittelpunktswinkel  doppelt so groß wie der eingeschriebene Winkel
doppelt so groß wie der eingeschriebene Winkel  .
.
Berechne die eingeschriebenen Winkel der folgenden Figuren
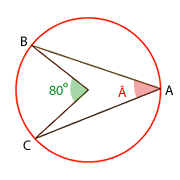


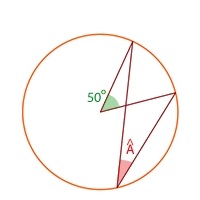


Dieses Feld ist erforderlich.
Da der Winkel 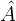 eingeschrieben ist, misst er die Hälfte des Bogens, den er aufspannt. Aus der Abbildung ist ersichtlich, dass der aufgespannte Bogen
eingeschrieben ist, misst er die Hälfte des Bogens, den er aufspannt. Aus der Abbildung ist ersichtlich, dass der aufgespannte Bogen 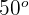 misst. Somit:
misst. Somit:

Da der Winkel 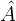 eingeschrieben ist, misst er die Hälfte des Bogens, den er aufspannt. Aus der Abbildung ist ersichtlich, dass der aufgespannte Bogen
eingeschrieben ist, misst er die Hälfte des Bogens, den er aufspannt. Aus der Abbildung ist ersichtlich, dass der aufgespannte Bogen 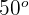 misst. Somit:
misst. Somit:
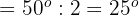
Der abgebildete Kreis wurde in 6 gleiche Teile geteilt. Berechne das Maß des Innenwinkels
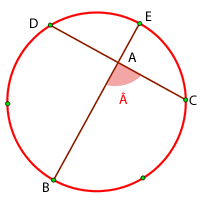


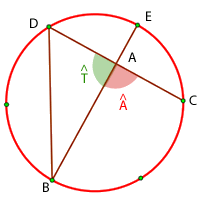
Der Kreis unten zeigt die Maße der Innenbögen eines Innenwinkels und seines Gegenstücks. Berechne das Maß des Winkels
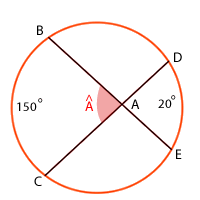


Dieses Feld ist erforderlich.
Da der Kreis in 6 gleiche Teile unterteilt ist, misst jeder Teil 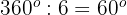 . Wenn wir
. Wenn wir  mit
mit  verbinden, erhalten wir das Dreieck
verbinden, erhalten wir das Dreieck 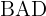 , bei dem folgende Winkel bekannt sind:
, bei dem folgende Winkel bekannt sind:
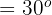 , da der Winkel eingeschrieben ist und sein Bogen eine Division ist
, da der Winkel eingeschrieben ist und sein Bogen eine Division ist
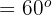 , da der Winkel eingeschrieben ist und sein Bogen zwei Divisionen sind
, da der Winkel eingeschrieben ist und sein Bogen zwei Divisionen sind
Also: 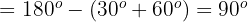
Da  und
und 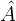 Supplementwinkel sind, gilt
Supplementwinkel sind, gilt 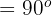
Für den zweiten Kreis verfahren wir wie oben beschrieben
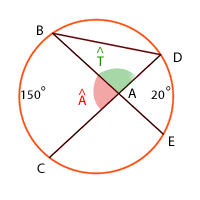
Wir wissen, dass 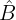 ein eingeschriebener Winkel ist, dessen Bogen
ein eingeschriebener Winkel ist, dessen Bogen 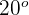 misst und er somit
misst und er somit 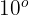 misst
misst
 , da der Winkel eingeschrieben ist und sein Bogen
, da der Winkel eingeschrieben ist und sein Bogen 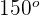 misst
misst

Da  und
und 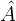 Supplementwinkel sind, gilt
Supplementwinkel sind, gilt 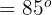
Mit KI zusammenfassen:


