Löse die folgenden Probleme:
Berechne die Oberfläche des folgenden Trapezes.
Dieses Feld ist erforderlich.
1 Wir sehen, dass es sich um ein Trapez handelt
2 Wir drücken alle Maße in derselben Einheit aus
Kleinere Grundseite 
Gößere Grundseite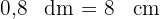 
Höhe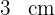 
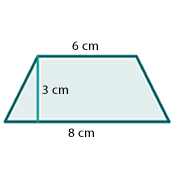
3 Wir setzen die Werte in die Formel für den Flächeninhalt eines Trapezes ein
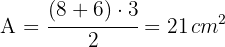
Ein Grundstück hat die folgende Trapezform. Seine größere Grundseite misst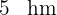 
und seine Höhe 
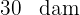. Die Fläche des genannten Grundstücks beträgt 
Hektar. Wie lange ist die kleinere Grundseite des Grundstücks?
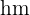
Dieses Feld ist erforderlich.
1 Wir sehen, dass es sich um ein Trapez handelt
2 Wir drücken alle Maße in derselben Einheit aus.
Höhe 
Größere Grundseite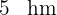
Fläche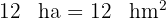 
3 Wenn also 
das Maß der kleineren Grundseite ist, ist die Fläche des Grundstücks wie folgt gegeben
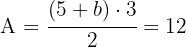
Wir lösen nach auf und erhalten 
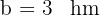
Wie groß ist der Flächeninhalt eines rechtwinkligen Dreiecks, dessen Katheten 
und 
messen?
Dieses Feld ist erforderlich.
1Der Flächeninhalt eines rechtwinkligen Dreiecks ist gleich der Hälfte des Produkts der Katheten
2Aus den angegebenen Werten ergibt sich, dass die Katheten und messen
3Wir setzen die Werte in die Formel für den Flächeninhalt eines Dreiecks ein
Betrachte die folgende Abbildung und berechne die Fläche des Dreiecks, das den Weihnachtsbaum einrahmt.
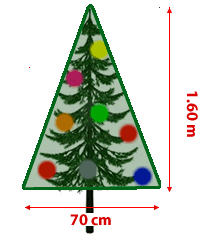
Der gesuchte Flächeninhalt ist 
Dieses Feld ist erforderlich.
1Der Flächeninhalt eines Dreiecks ist gleich der Hälfte des Produkts aus Basis und Höhe
2Aus den angegebenen Werten ergibt sich, dass die Basis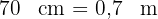 
und die Höhe 
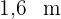misst
3Wir setzen in die Formel für den Flächeninhalt eines Dreiecks ein und erhalten
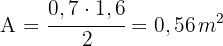
Gegeben ist ein Quadrat mit einem Flächeninhalt von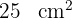 
. Kannst du sagen, wie groß der Flächeninhalt jedes der Dreiecke ist, die durch das Einzeichnen der Diagonalen dieses Quadrats gebildet werden?
Dieses Feld ist erforderlich.
1Wenn wir die Diagonalen eines Quadrats einzeichnen, wird es in vier gleiche Dreiecke geteilt
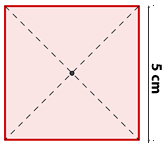
2Um den Flächeninhalt jedes Dreiecks zu erhalten, teilt man einfach den Flächeninhalt des Quadrats durch vier
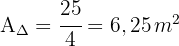
Gegeben sind drei gleichseitige Dreiecke mit einer Seitenlänge von 
. Sie sind so angeordnet, dass sie ein Trapez bilden.
Dieses Feld ist erforderlich.
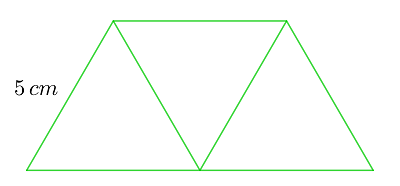
1Die Fläche eines gleichseitigen Dreiecks ist gegeben durch
2Wir setzen die Seite von in die Formel für den Flächeninhalt ein
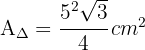
3Somit ist der Flächeninhalt des Trapezes
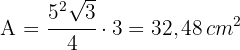
Ein gleichseitiges Dreieck mit der Seitenlänge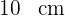 
wird in den Mittelpunkten von zwei seiner Seiten geschnitten, um ein Trapez zu bilden. Wie groß ist die kleinere Grundseite des Trapezes?
Dieses Feld ist erforderlich.
1Wir zeichnen Segmente, deren Enden in den Mittelpunkten des gleichseitigen Dreiecks liegen
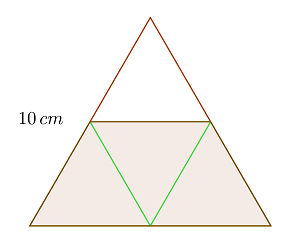
2Man erhält vier gleiche gleichseitige Dreiecke mit einer Seitenlänge von jeweils
3Somit misst die kleinere Grundseite des Trapezes
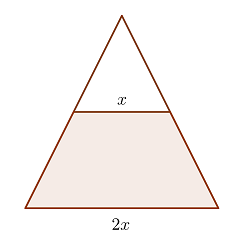
Gegeben ist ein Trapez mit einer größeren Grundseite, die das Doppelte der kleineren Grundseite misst. Seine nicht parallelen Seiten werden so verlängert, dass sie ein Dreieck bilden. Wenn die Fläche des Dreiecks, dessen Grundseite die kleinere Grundseite des Trapezes ist,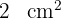 
misst, wie groß ist dann die Fläche des größeren Dreiecks?
Dieses Feld ist erforderlich.
1Beide Dreiecke sind ähnlich
2Das Ähnlichkeitsverhältnis zwischen seinen Grundseiten ist
3Bei zwei ähnlichen Dreiecken ist das Verhältnis ihrer Flächen gleich dem Quadrat des Verhältnisses ihrer Seiten
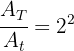
Da die Fläche des kleineren Dreiecks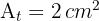 
ist, beträgt die Fläche 
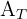des größeren Dreiecks
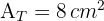
Gegeben ist ein Trapez, dessen größere Grundseite das Dreifache seiner kleineren Grundseite misst. Seine nicht parallelen Seiten werden so verlängert, dass sie ein Dreieck bilden. Wenn die Fläche des Dreiecks, dessen Grundseite die kleinere Grundseite des Trapezes ist, 
misst, wie ist dann der Flächeninhalt des Trapezes?
Dieses Feld ist erforderlich.
1Die beiden Dreiecke sind ähnlich
2Das Ähnlichkeitsverhältnis zwischen seinen Grundseiten ist
3Bei zwei ähnlichen Dreiecken ist das Verhältnis ihrer Flächen gleich dem Quadrat des Verhältnisses ihrer Seiten
Da die Fläche des kleineren Dreiecks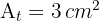 
ist, beträgt der Flächeninhalt 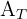des größeren Dreiecks
4Die Fläche des Trapezes ist also gleich der Differenz der Flächen der Dreiecke
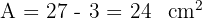
Gegeben ist ein Sechseck mit einem Flächeninhalt von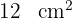 
. Wir verlängern zwei Seiten, um ein Trapez zu erhalten. Wie lautet der Flächeninhalt des Trapezes?
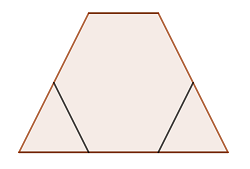
Dieses Feld ist erforderlich.
1Wir unterteilen das Sechseck in sechs gleiche Dreiecke
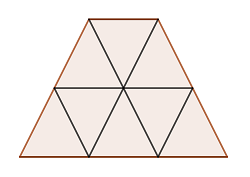
2Der Flächeninhalt jedes der Dreiecke ist
3Zwei Dreiecke mit dem Flächeninhalt 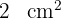bilden zusammen das Trapez
4Somit ist der Flächeninhalt des Trapezes
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
