Löse die folgenden Probleme:
Die Hypotenuse eines rechtwinkligen Dreiecks misst  cm und eine seiner Katheten misst
cm und eine seiner Katheten misst  cm. Wie lange ist die andere Kathete
cm. Wie lange ist die andere Kathete
cm
Dieses Feld ist erforderlich.
Wir wenden den Satz des Pythagoras an:
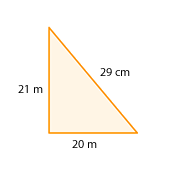

Wir haben zwei Dreiecke. Ein Dreieck  mit den Maßen
mit den Maßen 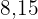 und
und  und ein weiteres
und ein weiteres 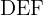 mit den Maßen
mit den Maßen  und
und  . Schreibe „ja“ oder „nein“, um anzugeben, ob die Dreiecke rechtwinklig sind oder nicht..
. Schreibe „ja“ oder „nein“, um anzugeben, ob die Dreiecke rechtwinklig sind oder nicht..

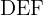
Dieses Feld ist erforderlich.
In beiden Fällen überprüfen wir, ob der Satz des Pythagoras erfüllt ist oder nicht. Dazu müssen wir berücksichtigen, dass die Hypotenuse, sofern vorhanden, immer die längste Seite ist..
1 Wir führen die Berechnung für das Dreieck  durch.
durch.

Der Satz des Pythagoras ist erfüllt, da das Dreieck  rechtwinklig ist.
rechtwinklig ist.
2 Wir führen die Berechnung für das Dreieck 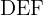 durch.
durch.

Der Satz des Pythagoras ist nicht erfüllt, da das Dreieck 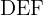 nicht rechtwinklig ist.
nicht rechtwinklig ist.
Eine 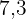 m hohe Leiter wird mit dem Fuß in
m hohe Leiter wird mit dem Fuß in 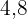 m Entfernung von der Wand aufgestellt, um ein Problem auf dem Dach eines Hauses zu beheben. In welcher Höhe befindet sich das Dach?
m Entfernung von der Wand aufgestellt, um ein Problem auf dem Dach eines Hauses zu beheben. In welcher Höhe befindet sich das Dach?
Dieses Feld ist erforderlich.
Wir wenden den Satz des Pythagoras für die Höhe  an
an
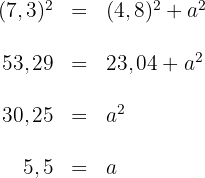
Somit befindet sich das Dach auf einer Höhe von 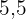 m.
m.

Die Katheten eines rechtwinkligen Dreiecks sind  bzw.
bzw.  cm lang. Wie lang ist die Hypotenuse? Runde auf zwei Dezimalstellen.
cm lang. Wie lang ist die Hypotenuse? Runde auf zwei Dezimalstellen.
h = cm.
Dieses Feld ist erforderlich.
Wir wenden den Satz des Pythagoras an, um die Hypotenuse  zu berechnen
zu berechnen
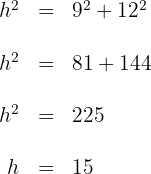
Die Hypotenuse misst  cm.
cm.
Berechne die Abbildungen  und
und  der Katheten auf der Hypotenuse. Runde, falls nötig auf zwei Dezimalstellen.
der Katheten auf der Hypotenuse. Runde, falls nötig auf zwei Dezimalstellen.
n = cm.
m = cm.
Dieses Feld ist erforderlich.
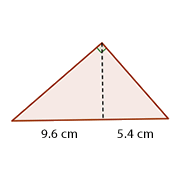
Wir wenden den Kathetensatz an, um die Maße der Abbildungen zu erhalten. 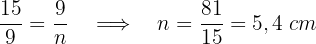
Die Abbildung der Kathete  misst
misst 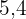 cm.
cm. 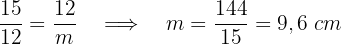
Die Abbildung der Kathete  misst
misst 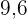 cm.
cm.
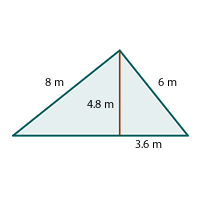
Zur Installation einer Satellitenschüssel wird ein Mast verwendet, der, wie in der Abbildung gezeigt, mit zwei Kabeln befestigt wird..
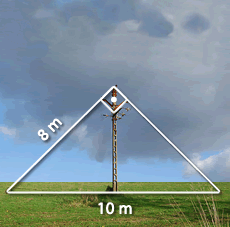
Gib das Maß des fehlenden Kabels an m.
In welcher Entfernung vom Mast muss dieses Kabel angebracht werden? m.
Dieses Feld ist erforderlich.
1 Da die beiden Kabel ein rechtwinkliges Dreieck bilden, berechnen wir die Länge des fehlenden Kabels mithilfe des Satzes des Pythagoras.
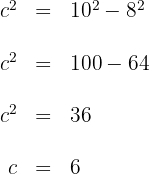
Das Kabel hat eine Länge von 6 m.
2 Um die Entfernung zu berechnen, in der das Kabel verlegt werden muss, wenden wir den Satz des Pythagoras an.
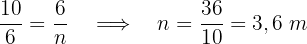
Wir müssen das Kabel in einer Entfernung von 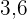 m vom Mast verlegen..
m vom Mast verlegen..
Wie hoch ist der Mast? m.
Dieses Feld ist erforderlich.
Um die Höhe des Mastes zu berechnen, wenden wir den Satz des Pythagoras auf das rechtwinklige Dreieck in der Abbildung an, dessen Hypotenuse  m und dessen Grundseite
m und dessen Grundseite  m misst..
m misst..
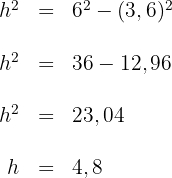
Die Höhe des Mastes beträgt  m.
m.
Mit KI zusammenfassen:


