Löse die folgenden Probleme zur Ähnlichkeit von Dreiecken. Wenn du noch Zweifel hast, kannst du dir hier die Theorie dazu ansehen:
1 Berechne die Seiten des ähnlichen Dreiecks
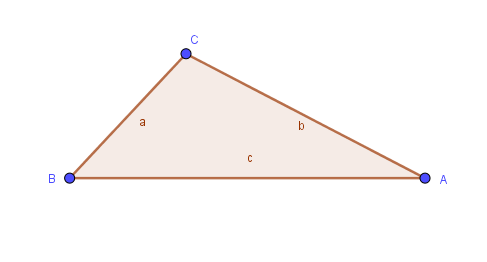
a  sei ein Dreieck mit den Seiten
sei ein Dreieck mit den Seiten 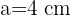 ,
, 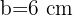 ,
, 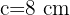 und dem Proportionalitätsverhältnis
und dem Proportionalitätsverhältnis 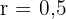 . Somit sind die Seiten des ähnlichen Dreiecks:
. Somit sind die Seiten des ähnlichen Dreiecks:
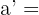

Dieses Feld ist erforderlich.
Die Dreiecke sind zueinander ähnlich, da ihre Seiten proportional sind im Verhältnis 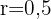 , also
, also 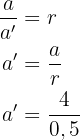
das heißt, 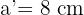 .
.
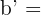

Dieses Feld ist erforderlich.
Und ebenfalls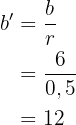
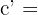

Dieses Feld ist erforderlich.
und schließlich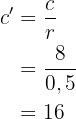
b sei ein Dreieck mit den Seiten
sei ein Dreieck mit den Seiten 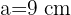 ,
, 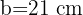 und
und 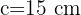 . Wenn wir von einem Verhältnis
. Wenn wir von einem Verhältnis 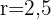 ausgehen, sind die Seiten des ähnlichen Dreiecks
ausgehen, sind die Seiten des ähnlichen Dreiecks 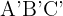 :
:
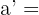

Dieses Feld ist erforderlich.
Ebenso sind die Dreiecke zueinander ähnlich, diesmal jedoch mit 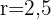
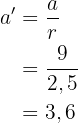
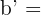

Dieses Feld ist erforderlich.
und 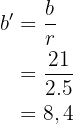
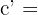

Dieses Feld ist erforderlich.
und schließlich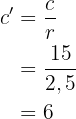
2Die Katheten eines rechtwinkligen Dreiecks messen 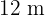 und
und 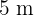 . Wie lang sind die Katheten eines rechtwinkligen Dreiecks, dessen Hypotenuse
. Wie lang sind die Katheten eines rechtwinkligen Dreiecks, dessen Hypotenuse 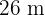 misst?
misst?
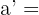

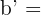

Dieses Feld ist erforderlich.
Zuerst berechnen wir die Hypotenuse des ersten rechtwinkligen Dreiecks mithilfe des Satzes des Pythagoras und anschließend berechnen wir die Katheten des zweiten Dreiecks anhand des Ähnlichkeitsverhältnisses.

Hypotenuse Dreieck 1:
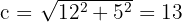 . Daraus folgt, dass
. Daraus folgt, dass 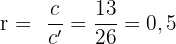
Mit diesem Verhältnis 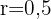 berechnen wir die Katheten des Dreiecks 2:
berechnen wir die Katheten des Dreiecks 2:
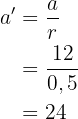 y
y
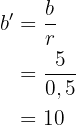
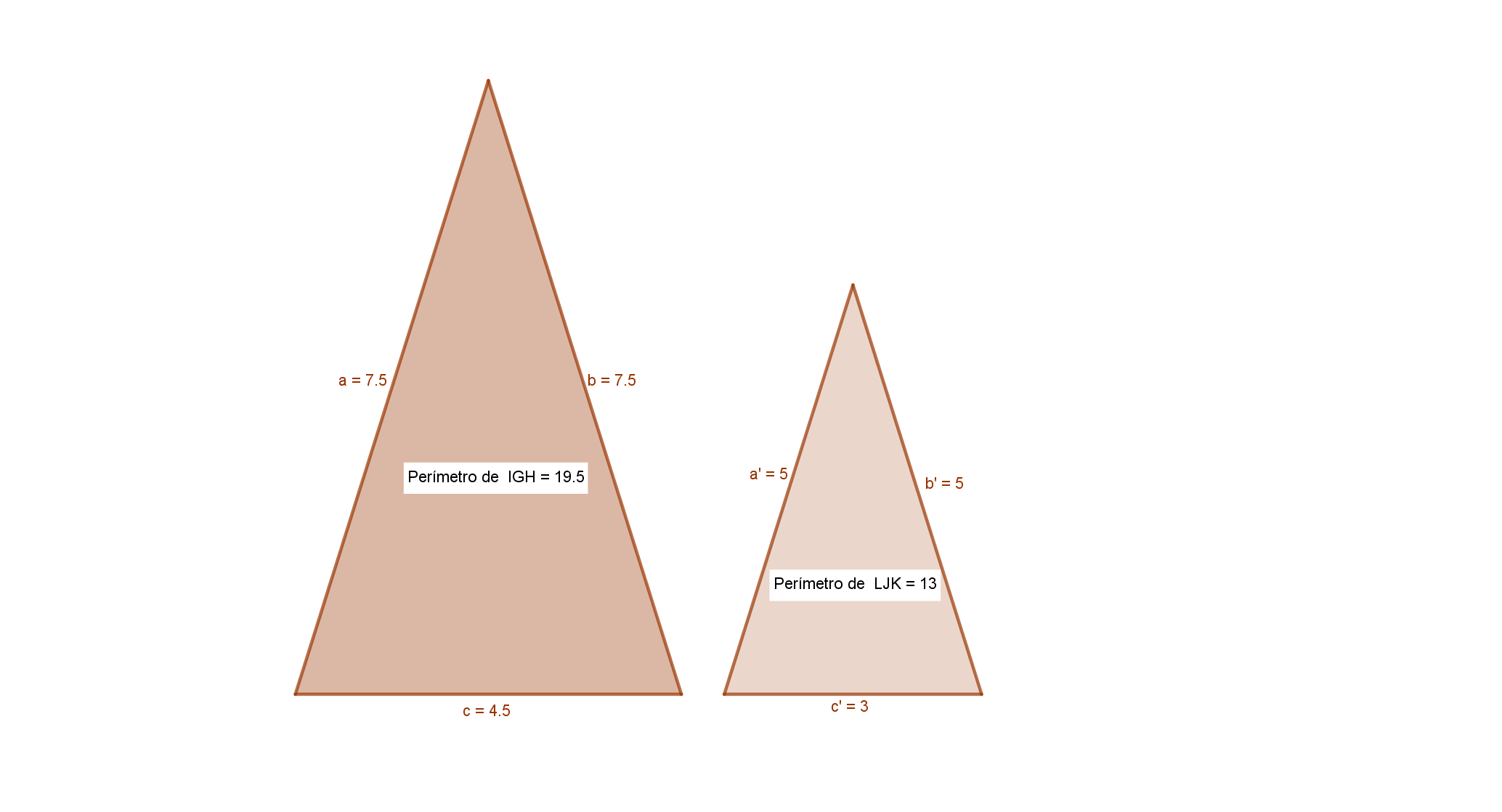
3Wir wissen, dass die Umfänge zweier ähnlicher gleichschenkliger Dreiecke 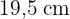 und
und 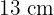 betragen und dass die ungleiche Seite des ersten Dreiecks
betragen und dass die ungleiche Seite des ersten Dreiecks 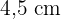 misst. Berechne die Seiten beider Dreiecke und das Ähnlichkeitsverhältnis.
misst. Berechne die Seiten beider Dreiecke und das Ähnlichkeitsverhältnis.
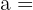

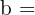

Dieses Feld ist erforderlich.
Zunächst berechnen wir die Seiten des Dreiecks, von dem wir die ungleiche Seite kennen. Da das Dreieck gleichschenklig ist, hat es zwei gleiche Seiten, also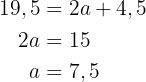
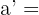

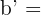

Dieses Feld ist erforderlich.
Da die Dreiecke zueinander ähnlich sind, wenden wir das Ähnlichkeitsverhältnis an: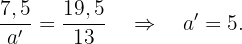
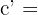

Dieses Feld ist erforderlich.
Da es sich um ein gleichschenkliges Dreieck handelt, sind a' und b' gleich lang und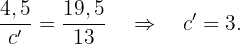
und schließlich 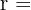 .
.
Dieses Feld ist erforderlich.
Für das Verhältnis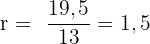
Da die Fläche des ersten Dreiecks 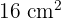 beträgt, berechne die Fläche des zweiten Dreiecks, ohne dessen Seiten zu verwenden
beträgt, berechne die Fläche des zweiten Dreiecks, ohne dessen Seiten zu verwenden
Fläche: 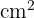
Dieses Feld ist erforderlich.
Zur Berechnung der Fläche verwenden wir das Ähnlichkeitsverhältnis zu den Flächen (das quadratisch ist):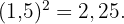
Also 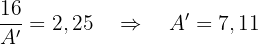
4 Berechne die Höhe eines Gebäudes, das einen Schatten von 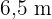 wirft, während gleichzeitig ein
wirft, während gleichzeitig ein 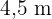 hoher Mast einen Schatten von
hoher Mast einen Schatten von 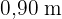 wirft.
wirft.
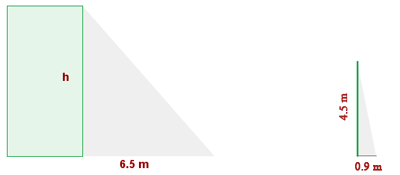
Höhe des Gebäudes:
Dieses Feld ist erforderlich.
Da die Schatten zur gleichen Zeit geworfen werden, nehmen wir eine Ähnlichkeit an, um eine Lösung zu finden. Angesichts dieser Ähnlichkeit erhalten wir folgende Gleichung
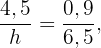
wir berechnen  und erhalten
und erhalten
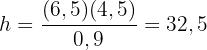
5 Wie lautet das Verhältnis der folgenden Dreiecke? 
Verhältnis: 
Dieses Feld ist erforderlich.
Wir können ein beliebiges Paar homologer Seiten nehmen, zum Beispiel die Seiten b und b', und berechnen ihr Verhältnis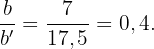
6 Im weiteren Verlauf haben wir 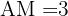 ,
,  ,
, 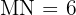 und
und 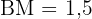
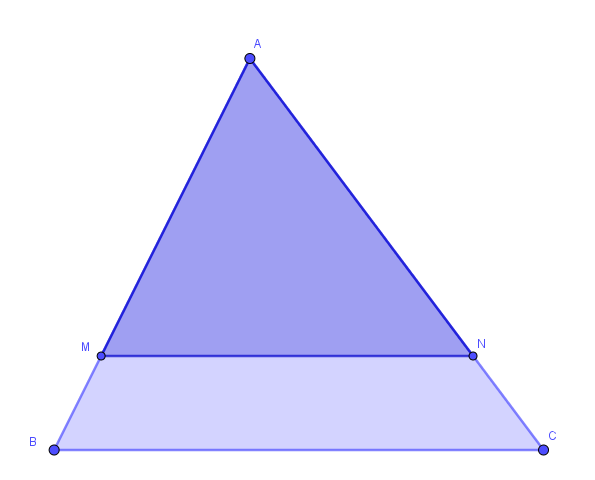
Wie lang ist 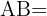 ?
?
Dieses Feld ist erforderlich.
Für  gilt
gilt 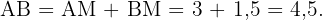
Wie lang ist 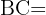 ?
?
Dieses Feld ist erforderlich.
Da es sich jedoch um ähnliche Dreiecke handelt, haben wir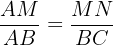
somit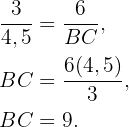
Wie lang ist 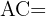 ?
?
Dieses Feld ist erforderlich.
Und auch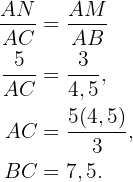
7 sei ein gleichschenkliges Dreieck, dessen ungleiche Seite
sei ein gleichschenkliges Dreieck, dessen ungleiche Seite  misst und
misst und 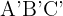 sei ein ähnliches gleichschenkliges Dreieck, dessen ungleiche Seite
sei ein ähnliches gleichschenkliges Dreieck, dessen ungleiche Seite  misst. Die anderen beiden Seiten (die gleich sind) messen
misst. Die anderen beiden Seiten (die gleich sind) messen 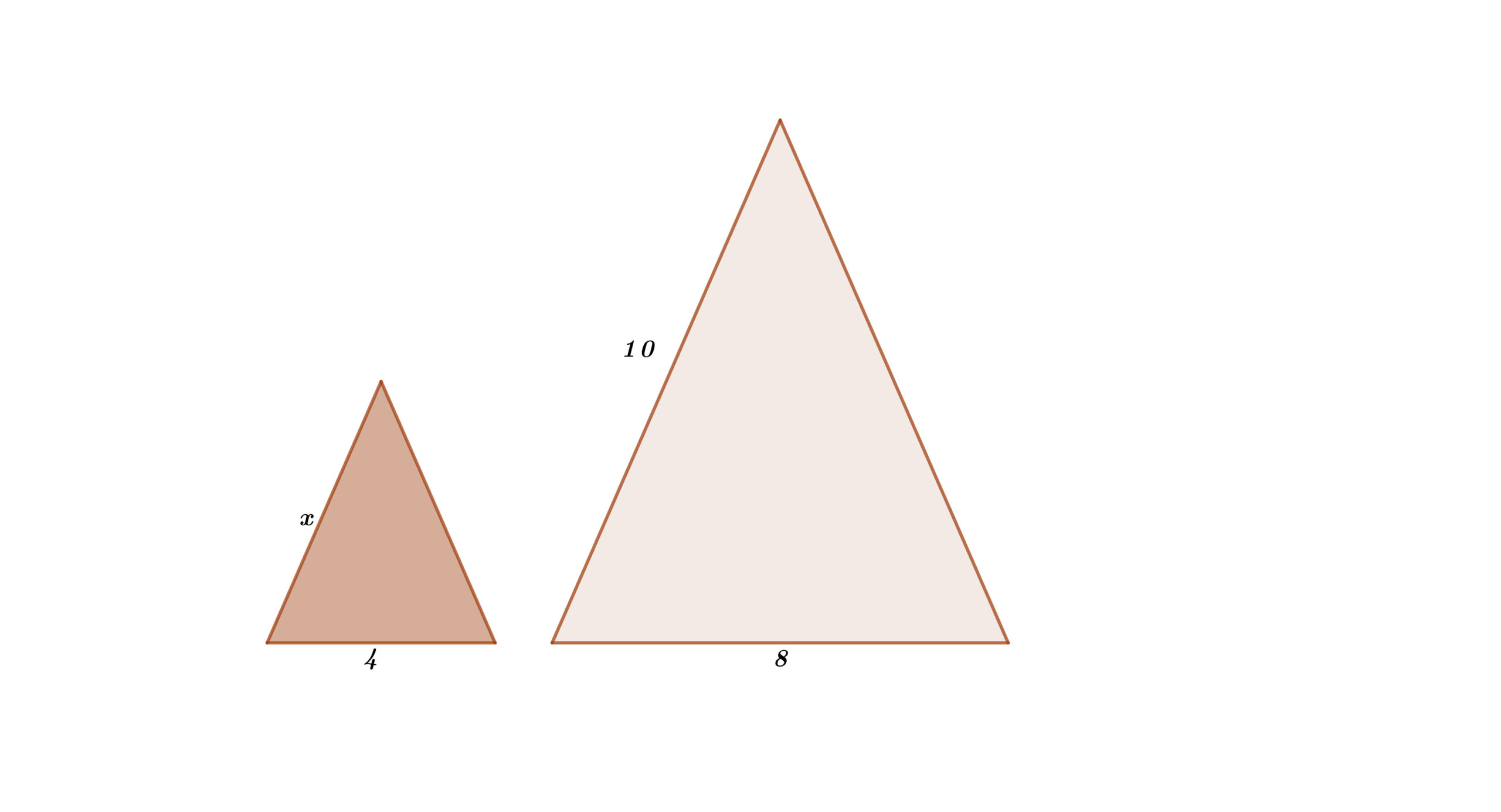
Wie lang sind die fehlenden Seiten von  ?
?
Dieses Feld ist erforderlich.
Da es sich um zueinander ähnliche Dreiecke handelt, haben wir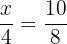
somit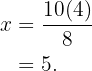
Mit KI zusammenfassen:


