Löse die folgenden Probleme:
Berechne den Flächeninhalt der folgenden Figur:
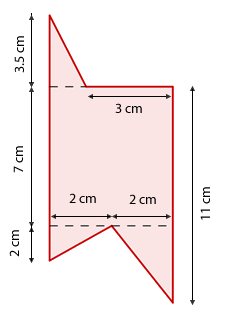
Die gesuchte Fläche ist cm².
Dieses Feld ist erforderlich.
Zunächst berechnen wir die fehlenden Maße, um die Figur in Dreiecke zu unterteilen:
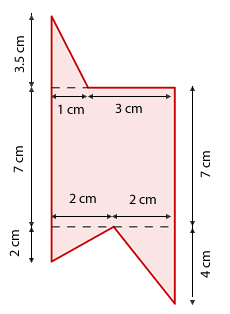
Nun unterscheiden wir die drei Dreiecke, die wir erkennen können sowie das zentrale Rechteck und berechnen die Fläche jedes einzelnen. Die Gesamtfläche entspricht der Summe aller Flächen. 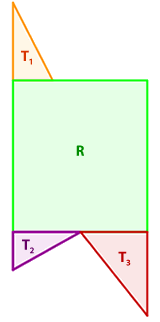
Der Flächeninhalt eines Dreiecks beträgt 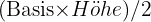 und die Fläche eines Rechtecks
und die Fläche eines Rechtecks 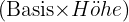 .
.
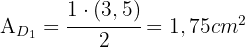
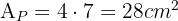
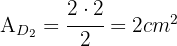
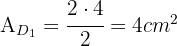
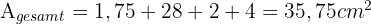
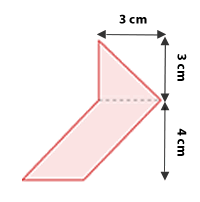
Berechne den Flächeninhalt der folgenden Figur.
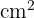
Dieses Feld ist erforderlich.
Wir können die Figur in ein Dreieck mit der Basis  und der Höhe
und der Höhe  sowie ein Parallelogramm mit der Grundseite
sowie ein Parallelogramm mit der Grundseite  und der Höhe
und der Höhe  unterteilen. Also berechnen wir die Flächen des Dreiecks und des Parallelogramms, um sie anschließend zu addieren und die Gesamtfläche zu erhalten.
unterteilen. Also berechnen wir die Flächen des Dreiecks und des Parallelogramms, um sie anschließend zu addieren und die Gesamtfläche zu erhalten.
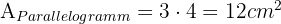 .
.
Die Fläche des Parallelogramms ist 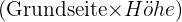 .
.
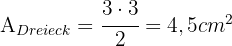 .
.
Die Fläche eines Dreiecks ist 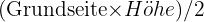
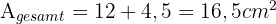
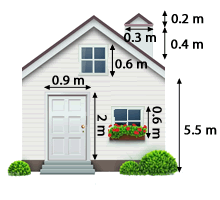
Wir möchten den Teil der Fassade und den Kamin des Hauses streichen, die auf dem Bild zu sehen sind. Wir wissen, dass die Fläche der Fassade einschließlich der Tür und der Fenster 55 m² beträgt und dass der Kamin aus einem Rechteck von 0,4 m x 0,3 m und einem Dreieck besteht. Ein 1-kg-Eimer Farbe kostet 3 €.
Wenn man weiß, dass mit 1 kg Farbe etwa 8 m² gestrichen werden können und die kleinste verkaufte Farbdose 1 kg enthält, wie viel kostet dann die benötigte Farbe?
Dieses Feld ist erforderlich.
Zunächst berechnen wir die Fläche des Bereichs, den wir streichen wollen.
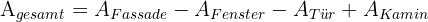
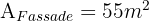
Da wir zwei quadratische Fenster haben, gilt
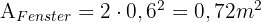
Da die Tür rechteckig ist, gilt
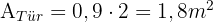
Der Kamin besteht aus einem Rechteck und einem Dreieck, also
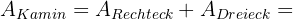
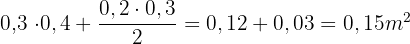
Wenn wir die entsprechenden Flächen addieren und subtrahieren, erhalten wir
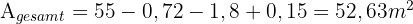
Da mit 1 kg Farbe 8 m² gestrichen werden können, benötigen wir
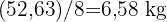
Da das Minimum, das wir kaufen können, 1 kg ist, fehlen noch 7 kg.
Die Kosten liegen bei 
 €
€
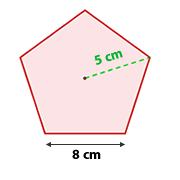
Berechne die Fläche eines regelmäßigen Fünfecks mit einer Seitenlänge von 8 cm und einem Radius von 5 cm.
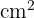
Und die Fläche eines regelmäßigen Achtecks mit einer Seitenlänge von 8 cm und einem Apothema von 6 cm.
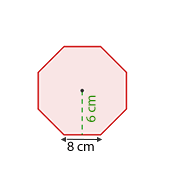
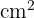
Dieses Feld ist erforderlich.
Erinnern wir uns daran, dass die Fläche eines regelmäßigen Vielecks 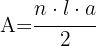 ist, wobei
ist, wobei  die Anzahl der Seiten,
die Anzahl der Seiten,  die Länge einer Seite und
die Länge einer Seite und  das Apothema ist, das als das Segment definiert ist, das den Mittelpunkt des Vielecks mit dem Mittelpunkt einer Seite verbindet. In unserem Fall ist ein Fünfeck ein regelmäßiges Vieleck mit
das Apothema ist, das als das Segment definiert ist, das den Mittelpunkt des Vielecks mit dem Mittelpunkt einer Seite verbindet. In unserem Fall ist ein Fünfeck ein regelmäßiges Vieleck mit  Seiten und ein Achteck ein regelmäßiges Vieleck mit
Seiten und ein Achteck ein regelmäßiges Vieleck mit  Seiten. Wir wenden also die obige Formel an, um ihre Flächen zu berechnen.
Seiten. Wir wenden also die obige Formel an, um ihre Flächen zu berechnen.
Fläche des Fünfecks
Zuerst müssen wir die Länge des Apothemas berechnen. Dazu ermitteln wir die Höhe eines gleichschenkligen Dreiecks mit zwei Seiten von 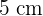 und einer Seite von
und einer Seite von 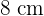 . Um die Höhe zu berechnen, verwenden wir den Satz des Pythagoras.
. Um die Höhe zu berechnen, verwenden wir den Satz des Pythagoras.
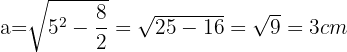


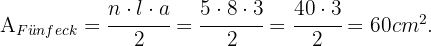
Fläche des Achtecks
Im Fall des Achtecks wird uns bereits der Wert des Apothemas angegeben, der 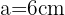 ist. Da das Achteck
ist. Da das Achteck  Seiten mit einer Seitenlänge von
Seiten mit einer Seitenlänge von 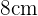 hat, gilt
hat, gilt
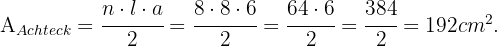
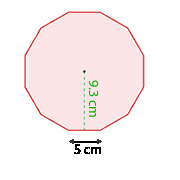
Wie groß ist die Fläche eines regelmäßigen Zwölfecks mit einer Seitenlänge von 5 cm und einem Apothema von 9,3 cm?
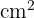
Dieses Feld ist erforderlich.
Da ein Zwölfeck ein regelmäßiges Vieleck mit  Seiten ist, berechnen wir seine Fläche mit der folgenden Formel
Seiten ist, berechnen wir seine Fläche mit der folgenden Formel 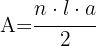 , wobei
, wobei  die Anzahl der Seiten,
die Anzahl der Seiten,  die Länge einer Seite und
die Länge einer Seite und  das Apothema ist, das als das Segment definiert ist, das den Mittelpunkt des Vielecks mit dem Mittelpunkt einer Seite verbindet. Da das Apothema
das Apothema ist, das als das Segment definiert ist, das den Mittelpunkt des Vielecks mit dem Mittelpunkt einer Seite verbindet. Da das Apothema 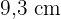 und eine Seite
und eine Seite 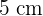 misst, gilt
misst, gilt
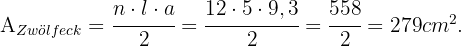
Mit KI zusammenfassen:


