Löse die folgenden Probleme:
Berechne die Höhe eines rechtwinkligen Dreiecks anhand der in der Abbildung angegebenen Werte: 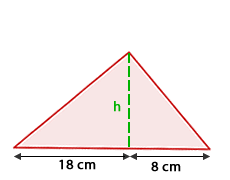


Dieses Feld ist erforderlich.
1 Wir wenden den Höhensatz an: 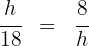
2 Wir berechnen 
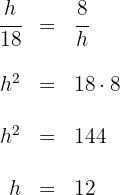
Die gesuchte Höhe ist
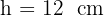
Berechne die Höhe eines rechtwinkligen Dreiecks anhand der in der Abbildung angegebenen Werte:
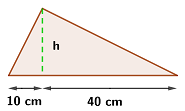


Dieses Feld ist erforderlich.
1 Wir wenden den Höhensatz an: 
2 Wir berechnen 
 Die gesuchte Höhe ist
Die gesuchte Höhe ist
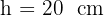
In einem rechtwinkligen Dreieck beträgt die zur Hypotenuse gehörende Höhe 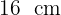 und die orthogonale Abbildung einer der Katheten
und die orthogonale Abbildung einer der Katheten 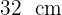 . Wie lang ist die Hypotenuse dieses Dreiecks?
. Wie lang ist die Hypotenuse dieses Dreiecks?
 .
.
Dieses Feld ist erforderlich.
1Wir stellen das Problem grafisch dar
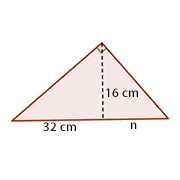
2Wir wenden den Höhensatz an:  Die Abbildung misst
Die Abbildung misst  .
.
3Somit misst die Hypotenuse 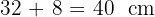 .
.
In einem rechtwinkligen Dreieck beträgt die zur Hypotenuse gehörende Höhe 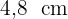 und die größere Kathete misst
und die größere Kathete misst  . Wie lang ist die Hypotenuse dieses Dreiecks?
. Wie lang ist die Hypotenuse dieses Dreiecks?
 .
.
Dieses Feld ist erforderlich.
1Wir stellen das Problem grafisch dar
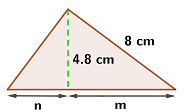
2Wir wenden den Satz des Pythagoras an: 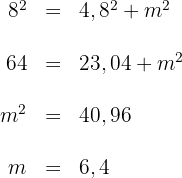 Die Abbildung der uns bekannten Kathete misst
Die Abbildung der uns bekannten Kathete misst 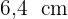 .
.
3Wir wenden den Höhensatz an: 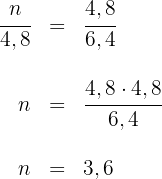
4Somit misst die Hypotenuse 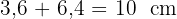 .
.
Die Katheten eines rechtwinkligen Dreiecks sind 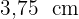 und
und  lang. Wie hoch ist die zur Hypotenuse gehörende Höhe dieses Dreiecks?
lang. Wie hoch ist die zur Hypotenuse gehörende Höhe dieses Dreiecks?
 .
.
Dieses Feld ist erforderlich.
1Wir stellen das Problem grafisch dar
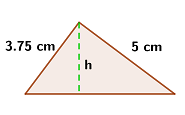
2Wir wenden den Satz des Pythagoras an: 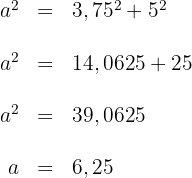 Die Hypotenuse misst
Die Hypotenuse misst 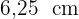 .
. 
3Wir wenden den Kathetensatz an 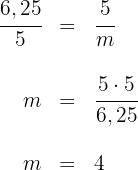 Luego, la otra proyección mide
Luego, la otra proyección mide 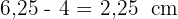 .
.
4Wir wenden den Höhensatz an: 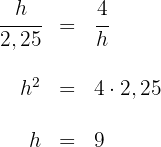 Somit misst die Höhe
Somit misst die Höhe 
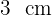 .
.
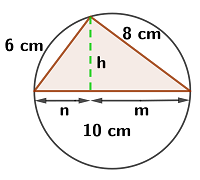
6 Ein rechtwinkliges Dreieck wird in einen Kreis mit dem Radius  eingeschrieben. Die Seite
eingeschrieben. Die Seite  misst
misst  , wie in der Abbildung zu sehen ist.
, wie in der Abbildung zu sehen ist.
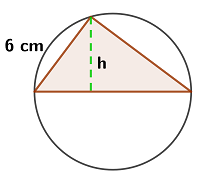
Berechne die Länge der Hypotenuse 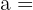
 .
.
Dieses Feld ist erforderlich.
In einem Kreis ist für jedes eingeschriebene rechtwinklige Dreieck die Hypotenuse gleich dem Durchmesser des Kreises. Die Hypotenuse misst also 
Wie lang muss die fehlende Seite sein?
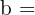
 .
.
Dieses Feld ist erforderlich.
Wir wenden den Satz des Pythagoras an: 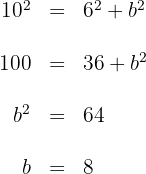
Wie hoch ist die zur Hypotenuse gehörende Höhe?

 .
.
Dieses Feld ist erforderlich.
Wir wenden den Kathetensatz an
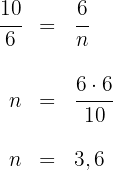
Die andere Abbildung misst 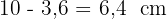
Wir wenden den Höhensatz an
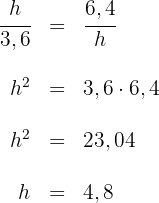
7Ein Schiffsmodell verwendet zwei kleine Seile, um den Großmast zu spannen, wie in der Abbildung gezeigt. 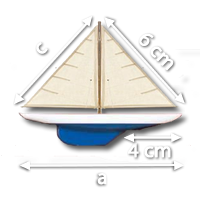
Berechne die Entfernung, in der wir das Seil  anbringen müssen.
anbringen müssen.  .
.
Dieses Feld ist erforderlich.
Zunächst einmal sehen wir, dass es sich um ein rechtwinkliges Dreieck handelt, sodass wir den Katheten- und den Höhensatz anwenden können.
Wir wenden den Kathetensatz an, um die Entfernung zu berechnen, in der sich das zweite Seil befinden muss:
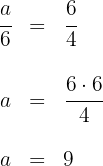
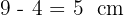
Das zweite Seil muss in einem Abstand von  zur Mastbasis angebracht werden.
zur Mastbasis angebracht werden.
Wie lang muss dieses Seil sein?
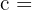
 .
.
Dieses Feld ist erforderlich.
Wir wenden den Kathetensatz an, um die Länge der Seite  zu berechnen:
zu berechnen:
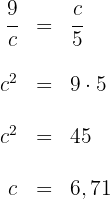
Die Seite  misst
misst 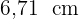
Kannst du sagen, wie hoch der Mast ist?
 .
.
Dieses Feld ist erforderlich.
Wir wenden den Höhensatz an, um die Höhe des Mastes zu berechnen:
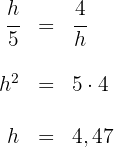
Der Mast hat eine Höhe von 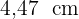
8Sieh dir die Rutsche an, auf der Lucia und Marco spielen. Berechne die Länge der Seite  .
.
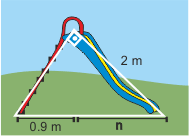

 .
.
Dieses Feld ist erforderlich.
Zunächst einmal sehen wir, dass es sich um ein rechtwinkliges Dreieck handelt, sodass wir den Katheten- und den Höhensatz anwenden können.
Wir wenden den Kathetensatz an, um  zu berechnen.
zu berechnen. 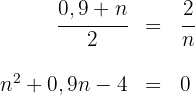
Wir lösen die quadratische Gleichung 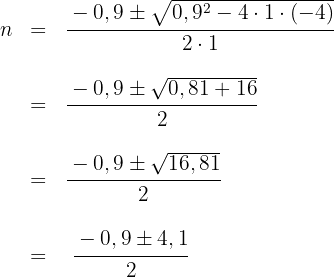
Wir erhalten die Nullstellen 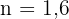 und
und 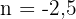 Von den beiden erhaltenen Lösungen ist nur die positive Lösung gültig, da die gesuchte Angabe ein Maß ist, das nicht negativ sein kann. Die gesuchte Entfernung ist also
Von den beiden erhaltenen Lösungen ist nur die positive Lösung gültig, da die gesuchte Angabe ein Maß ist, das nicht negativ sein kann. Die gesuchte Entfernung ist also 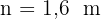
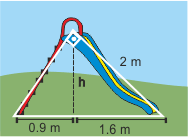
Wie hoch ist die Rutsche?  .
.
Dieses Feld ist erforderlich.
Wir wenden den Höhensatz an, um die Höhe der Rutsche zu berechnen.
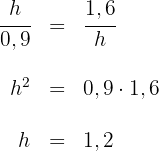
Somit beträgt die Höhe der Rutsche 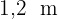 .
.
Mit KI zusammenfassen:


