
Definition des Kreises
Ein Kreis ist eine geschlossene gekrümmte Linie, deren Punkte alle gleich weit von einem festen Punkt, dem Mittelpunkt, entfernt sind, wie in der folgenden Abbildung dargestellt.
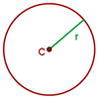
Elemente des Kreises
Mittelpunkt des Kreises
Der Punkt, von dem alle Punkte des Kreises gleich weit entfernt sind.
Radius der Kreislinie
Ein Segment, das den Mittelpunkt Kreises mit einem beliebigen Punkt des Kreises verbindet.
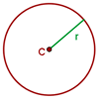
Sehne
Ein Segment, das zwei Punkte auf dem Kreis verbindet.

Durchmesser
Eine Sehne, die durch den Mittelpunkt des Kreises verläuft.
Bogen
Ein Kreisbogen ist jeder der Teile, in die eine Sehne den Kreis teilt.
Halbkreis
Jeder der gleichen Bögen, die einen Durchmesser umspannen.
Umfang eines Kreises
Dieser ist durch die Formel 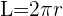 gegeben
gegeben
Länge eines Kreisbogens
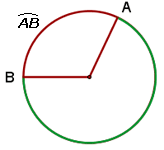
Ein Kreisbogen wird durch das Symbol 
Die Buchstaben werden gegen den Uhrzeigersinn geschrieben.
Länge eines Kreisbogens
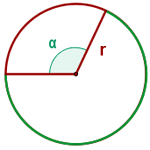
Diese ist durch die Formel 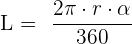 gegeben
gegeben
Aufgaben zu Kreisen
Berechne den Umfang eines Rades mit einem Durchmesser von 90 cm.
Sieh dir folgenden Kreis an
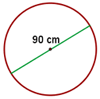
Um die Formel anwenden zu können, müssen wir den Radius kennen. Somit
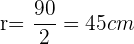
Nun können wir die Formel für den Kreisumfang anwenden
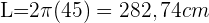
Berechne den Flächeninhalt des Quadrats, das in einen Kreis der Länge 18,84 cm eingeschrieben ist.
Gegeben ist folgende Abbildung
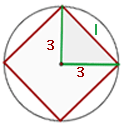
Wir setzen die Werte in die Formel des Kreisumfangs ein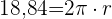
Wir können den Radius bestimmen, um den Wert der Seiten des Quadrats zu berechnen
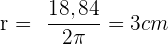
Wir wenden den Satz des Pythagoras an

Die Fläche des in den Kreis eingeschriebenen Quadrats beträgt also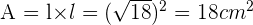
Die Arme einer Schaukel sind 1,80 m lang und können einen maximalen Winkel von 146° beschreiben. Berechne den Raum, den der Sitz der Schaukel einnimmt, wenn der Winkel, den die Schaukel beschreibt, maximal ist.
Wir setzen die Werte direkt in die Formel ein 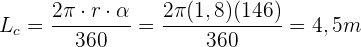
Ein Leuchtturm beschreibt mit seinem Licht einen flachen Winkel von 128°. Wenn die maximale Reichweite des Leuchtturms 7 Meilen beträgt, wie groß ist dann die maximale Länge des entsprechenden Bogens in Metern?
Es gilt: 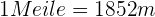 . Wir setzen in die Formel ein
. Wir setzen in die Formel ein 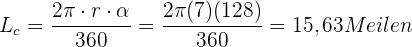 . Zuletzt rechnen wir noch Meilen in Meter um:
. Zuletzt rechnen wir noch Meilen in Meter um: 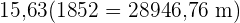
Kreiswinkel
Mittelpunktswinkel
Der Mittelpunktswinkel hat seinen Scheitelpunkt in der Mitte des Kreises und seine Seiten sind die beiden Radien.
Das Maß eines Bogens ist das Maß des entsprechenden Mittelpunktswinkels.
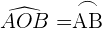
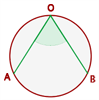
Umfangswinkel
Der Umfangswinkel hat seinen Scheitelpunkt auf dem Kreisumfang und seine Seiten sind Sekanten.
Er misst die Hälfte des Bogens, den er beschreibt.
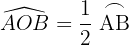
Sehnentangentenwinkel
Der Scheitelpunkt des Sehnentangentenwinkels befindet sich auf der Kreislinie. Eine Seite ist eine Sekante und die andere Seite ist eine Tangente.
Er misst die Hälte des Bogens, den er beschreibt.
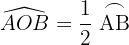
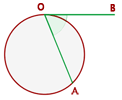
Innenwinkel
Sein Scheitelpunkt befindet sich innerhalb des Kreises und seine Seiten sind Sekanten.
Er misst die Hälfte der Summe der Maße der Bögen, die seine Seiten umspannen, und der Verlängerungen seiner Seiten.
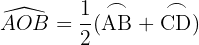
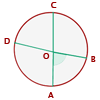
Außenwinkel
Sein Scheitelpunkt ist ein Punkt außerhalb des Kreises und die Seiten seiner Winkel sind: Sekanten oder eine Tangente und eine Sekante oder Tangenten:
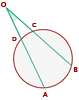
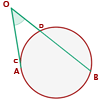

Er misst die Hälfte der Differenz zwischen den Maßen der Bögen, die seine Seiten auf der Kreislinie umspannen.
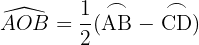
Mit KI zusammenfassen:












