Problemstellungen und Aufgaben zur Kreislinie und zum Kreis

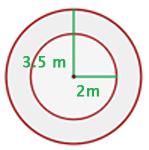
Anna reitet auf einem Pferd, das 3,5 m von der Mitte einer sich drehenden Plattform entfernt ist, und ihre Freundin Laura reitet auf einem Löwen, der 2 m von der Mitte entfernt ist. Berechne den Weg, den jeder von ihnen zurücklegt, wenn sich die Plattform 50 Mal dreht.

Wir berechnen die Strecke einer Runde mit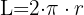

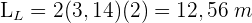
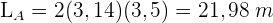
Die Gesamtstrecke ergibt sich aus der Multiplikation einer Runde mit 50

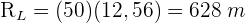
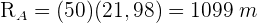
Die Seile einer Schaukel sind 1,8 m lang und können einen maximalen Winkel von 146° beschreiben. Berechne die Strecke, die der Sitz der Schaukel zurücklegt, wenn der Winkel, in dem die Schaukel schwingt, am größten ist.

Wir berechnen die Strecke für

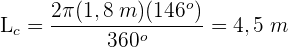
Das Rad eines LKWs hat einen Radius von 90 cm. Wie weit ist der LKW gefahren, wenn sich das Rad 100 Mal gedreht hat?

1 Wir rechnen den Radius in Meter um

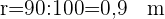
2 Wir berechnen die Strecke einer Umdrehung

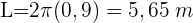
3 Wir berechnen die Strecke für 100 Umdrehungen

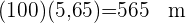
Ein Leuchtturm strahlt mit seinem Licht in einem flachen Winkel von 128°. Wenn die maximale Reichweite des Leuchtturms 7 Meilen beträgt, wie lang ist dann der entsprechende Lichtkegel in Metern?

1 Wir rechnen den Radius in Meter um, da eine Meile 1609,34 Metern entspricht

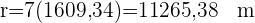
2 Wir berechnen die Strecke für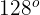

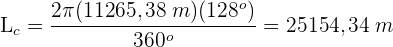
Der Umfang eines Kreises beträgt 43,96 cm. Wie groß ist der Flächeninhalt des Kreises?

1 Wir berechnen den Radius

2 Wir berechnen den Flächeninhalt des Kreises

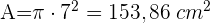
Die Fläche eines Kreissektors von 90° entspricht 4π Quadratzentimetern. Berechne den Radius des Kreises, zu dem er gehört, und die Länge der Kreislinie.

1 Wir berechnen den Radius

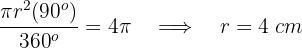
2 Wir berechnen die Länge der Kreislinie

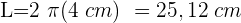
Bestimme die Fläche eines Kreissektors, dessen Sehne die Seite des eingeschriebenen gleichseitigen Dreiecks ist, wobei der Radius des Kreisumfangs 2 cm beträgt.

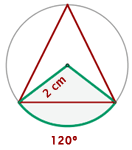
1 Der gesuchte Sektor entspricht einem Drittel der Gesamtfläche des Kreises, d. h. einem Sektor von

2 Wir berechnen die Fläche für

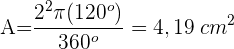
Gegeben sind zwei konzentrische Kreise mit jeweils 8 und 5 cm Durchmesser. Zeichne die Radien OA und OB, die einen Winkel von 60° bilden. Berechne den Flächeninhalt des gebildeten kreisförmigen Trapezes.

Wir berechnen die Fläche der zwei Sektoren und im Anschluss ihre Differenz.

In einem kreisförmigen Park mit einem Radius von 700 m befindet sich in der Mitte ein ebenfalls kreisförmiger Springbrunnen mit einem Radius von 5 m. Berechne die Fläche des Fußgängerbereichs.

Wir berechnen die Fläche der zwei Sektoren und im Anschluss ihre Differenz.

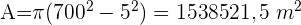
Die Oberfläche eines Tisches besteht aus einem quadratischen Mittelteil mit einer Seitenlänge von 1 m und zwei Halbkreisen, die an zwei gegenüberliegenden Seiten angebracht sind. Berechne den Flächeninhalt.

Wir berechnen die Fläche für den Sektor von

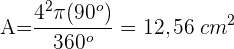
Ermittle die Fläche des Kreissektors, dessen Sehne die Seite des eingeschriebenen Quadrats ist, wobei 4 cm der Radius des Kreises ist.

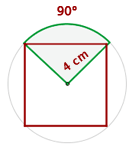
Wir berechnen die Fläche für den Sektor von

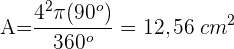
Berechne die schattierte Fläche, wobei du weißt, dass die Seitenlänge des Quadrats 6 cm und der Radius des Kreises 3 cm beträgt.

Wir berechnen die Fläche des Quadrats und des Kreises und dann die Differenz der beiden.

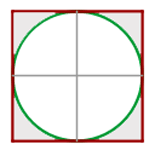
Auf einem kreisförmigen Platz mit einem Radius von 250 m sollen 7 Laternenmasten aufgestellt werden, deren Basen Kreise mit einem Radius von 1 m sind. Der Rest des Platzes soll für die Bepflanzung mit Rasen genutzt werden. Berechne die Fläche des Rasens.

Wir berechnen die Fläche des größeren Kreises, die Fläche der Laternenmasten und dann die Differenz dieser Flächen.

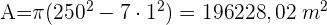
Berechne die Fläche des schattierten Teils, wenn der Radius des größeren Kreises 6 cm und der Radius der kleineren Kreise 2 cm beträgt.

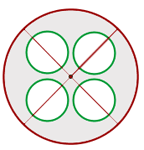
Wir berechnen die Fläche des größeren Kreises, die Fläche der kleineren Kreise und dann die Differenz dieser beiden.

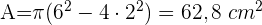
Berechne die Fläche des schattierten Bereichs, wobei AB = 10 cm ist, ABCD ein Quadrat ist und APC und AQC Kreisbögen mit den Mittelpunkten B und D sind.

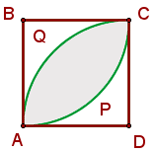
1Der schattierte Bereich setzt sich aus zwei Kreissegmenten zusammen:

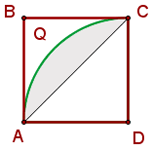
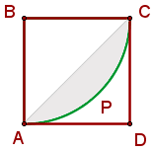
2 Wir berechnen die Fläche des Kreissegments und multiplizieren sie mit 2

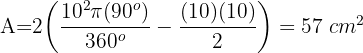
Ein regelmäßiges Sechseck mit der Seitenlänge 4 cm wird in einen Kreis eingeschrieben und von einem weiteren Kreis umschrieben. Bestimme die Fläche des so gebildeten Kreisrings.

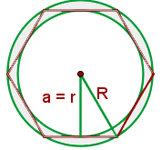
1 Wir berechnen den Radius des inneren Kreises, der mit dem Apothema des Sechsecks übereinstimmt

2 Wir berechnen die Fläche der einzelnen Kreise und dann die Differenz dieser Kreise

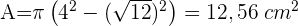
Die Sehne eines Kreises ist 48 cm lang und 7 cm vom Mittelpunkt entfernt. Berechne den Flächeninhalt des Kreises.

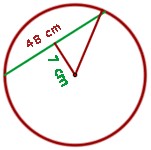
1 Wir berechnen den Radius des Kreises mit Hilfe des Satzes des Pythagoras

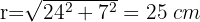
2 Wir berechnen die Fläche des Kreises

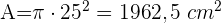
Die Schenkel eines in einen Kreis eingeschriebenen Dreiecks messen 22,2 cm bzw. 29,6 cm. Berechne den Flächeninhalt des Kreises.

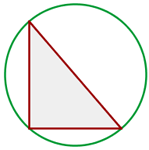
1 Wir berechnen die Fläche des Sektors

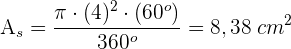
2 Berechne die Höhe des Dreiecks und den Flächeninhalt des Dreiecks

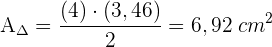
3 Wir berechnen die Differenz der Flächen

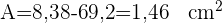
Ein Kreis mit dem Radius 4 cm hat einen Kreiswinkel von 60°. Bestimme die Fläche des Kreissegments zwischen der Sehne, die die Enden der beiden Radien verbindet, und dem entsprechenden Bogen.

1 Wir berechnen die Fläche des Sektors

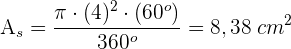
2 Berechne die Höhe des Dreiecks und den Flächeninhalt des Dreiecks

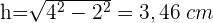
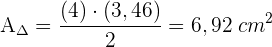
3 Wir berechnen die Differenz der Flächen

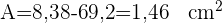
Gegeben ist ein gleichschenkliges Dreieck mit einer Seitenlänge von 6 m. Bestimme die Fläche eines der Sektoren, die durch den umschriebenen Kreis und die Radien, die durch die Eckpunkte verlaufen, bestimmt werden.

1 Der Mittelpunkt des Kreises ist der Schwerpunkt. Deshalb ist

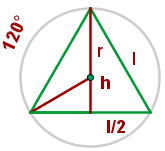
2 Wir berechnen die Höhe des Dreiecks und den Radius

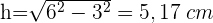
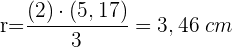
3 Wir berechnen die Fläche des Sektors

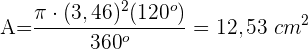
Berechne die Fläche des Kreisrings, die durch einen Inkreis und den Umkreis eines Qudrats definiert ist. Die Diagonale des Quadrats misst 8 m.

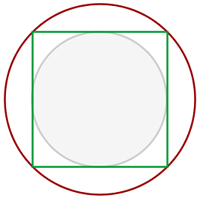
1 Wir berechnen den Radius des äußeren Kreises, dessen Durchmesser die Diagonale des Quadrats ist, und den Radius des inneren Kreises mit Hilfe des Satzes des Pythagoras

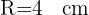
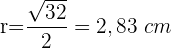
2 Wir berechnen die Differenz der Flächen