Die Hypotenuse eines rechtwinkligen Dreiecks misst 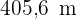 und die Projektion einer Kathete auf sie
und die Projektion einer Kathete auf sie 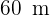 . Berechne die Katheten, die Höhe in Bezug auf die Hypotenuse und den Flächeninhalt des Dreiecks.
. Berechne die Katheten, die Höhe in Bezug auf die Hypotenuse und den Flächeninhalt des Dreiecks.
1 Wir stellen das Problem grafisch dar
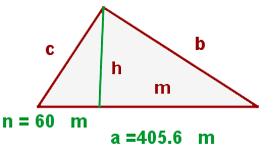
2 Wir stellen fest, dass sich zwei äquivalente Dreiecke ergeben, denn die Hypotenuse ist 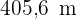 und die Projektion einer Kathete ist
und die Projektion einer Kathete ist 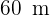 , d. h.
, d. h.
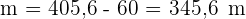
3 Für die Kathete  ergibt sich
ergibt sich
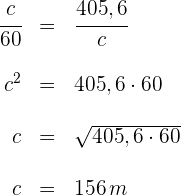
4 Für die Kathete  ergibt sich
ergibt sich
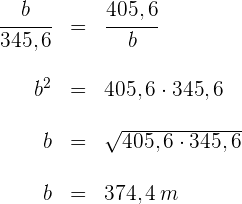
5 Für die Höhe  relativ zur Hyptenuse ergibt sich
relativ zur Hyptenuse ergibt sich
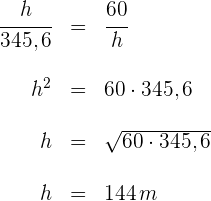
6 Die Fläche des Dreiecks ist
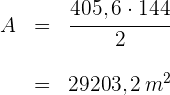
Berechne die Seiten eines rechtwinkligen Dreiecks, wenn du weißt, dass die Projektion einer der Katheten auf die Hypotenuse  und die relative Höhe dieser
und die relative Höhe dieser 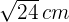 ist.
ist.
1 Wir stellen das Problem grafisch dar
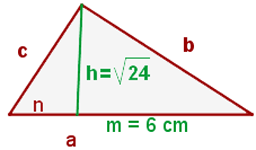
2 Wir stellen fest, dass sich zwei äquivalente Dreiecke ergeben und somit
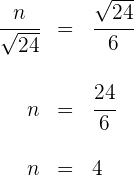
Somit misst die Hypotenuse
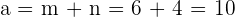
3 Für die Kathete  ergibt sich
ergibt sich
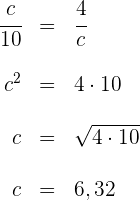
4 Für die Kathete  ergibt sich
ergibt sich
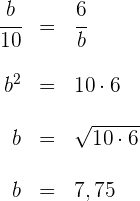
5 Somit sind die Seiten des Dreiecks: 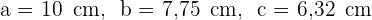
Eine 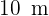 lange Leiter ist an eine Wand gelehnt. Der Fuß der Leiter befindet sich
lange Leiter ist an eine Wand gelehnt. Der Fuß der Leiter befindet sich 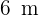 von der Wand entfernt. Wie hoch reicht die Leiter an der Wand?
von der Wand entfernt. Wie hoch reicht die Leiter an der Wand?
1 Wir stellen das Problem grafisch dar
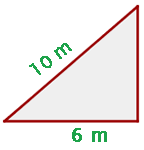
2 Wir stellen fest, dass diese Höhe mit dem Satz des Pythagoras ermittelt werden kann
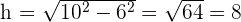
Die gesuchte Höhe ist somit 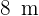
Bestimme die Seite eines gleichseitigen Dreiecks, dessen Umfang gleich dem eines Quadrats mit einer Seitenlänge von 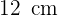 ist. Sind ihre Flächeninhalte gleich groß?
ist. Sind ihre Flächeninhalte gleich groß?
1

2 Sein Umfang ist 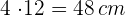 . Für die Berechnung des Flächeninhalts nutzen wir
. Für die Berechnung des Flächeninhalts nutzen wir
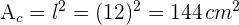
3 Das gleichseitige Dreieck hat drei gleiche Seiten. Wenn sein Umfang also 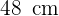 beträgt, dann misst jede seiner Seiten
beträgt, dann misst jede seiner Seiten 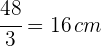
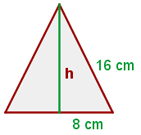
4 Um den Flächeninhalt zu ermitteln, müssen wir seine Höhe kennen. Dazu teilen wir das gleichseitige Dreieck in zwei rechtwinklige Dreiecke und wenden den Satz des Pythagoras an
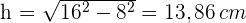
5 Wir berechnen den Flächeninhalt
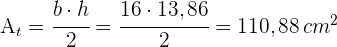
Die beiden Figuren haben also den gleichen Umfang, aber eine unterschiedlich große Fläche.
Berechne die Fläche eines gleichseitigen Dreiecks, das in einen Kreis mit dem Radius  eingeschrieben ist.
eingeschrieben ist.
1 Wir stellen das Problem grafisch dar
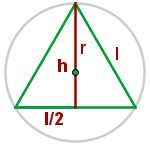
2 Der Mittelpunkt des Kreises ist der Schwerpunkt. Somit ist 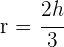 und wir erhalten
und wir erhalten
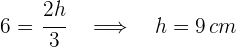
3 Um den Flächeninhalt des Dreiecks zu ermitteln, müssen wir seine Basis kennen. Dazu zerlegen wir das gleichseitige Dreieck in zwei rechtwinklige Dreiecke und wenden den Satz des Pythagoras an
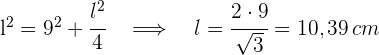
4 Wir berechnen den Flächeninhalt
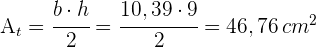
Berechne den Flächeninhalt eines Quadrats, das in einen Kreis mit der Länge 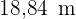 eingeschrieben ist.
eingeschrieben ist.
1 Wir stellen das Problem grafisch dar
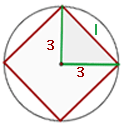
2 Wir müssen eine Seite des Quadrats kennen. Dazu berechnen wir zunächst den Radius anhand des Kreisumfangs
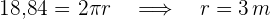
3 Um die Seite des Quadrats zu bestimmen, betrachten wir ein gleichschenkliges rechtwinkliges Dreieck, dessen gleiche Seiten die Radien des Kreisumfangs sind
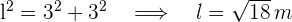
4 Die Fläche des Quadrats ist also
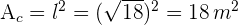
In ein Quadrat mit der Seitenlänge 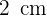 wird ein Kreis eingeschrieben. In diesen wird ein Quadrat und in dieses ein weiterer Kreis eingeschrieben. Bestimme die Fläche zwischen dem letzten Quadrat und dem letzten Kreis.
wird ein Kreis eingeschrieben. In diesen wird ein Quadrat und in dieses ein weiterer Kreis eingeschrieben. Bestimme die Fläche zwischen dem letzten Quadrat und dem letzten Kreis.
1 Wir stellen das Problem grafisch dar
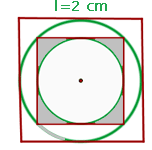
2 Wir müssen die Radien der Kreise kennen; Dazu stellen wir fest, dass die Seite des Quadrats der Seite 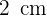 gleich dem Durchmesser des Inkreises ist.
gleich dem Durchmesser des Inkreises ist.
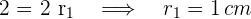
3 Der Durchmesser des ersten Kreises ist gleich der Diagonale des zweiten Quadrats. Durch Anwendung des Satzes des Pythagoras erhält man die Seitenlänge des zweiten Quadrats
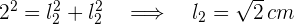
4 Somit ist die Fläche des zweiten Quadrats
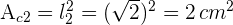
5 Der Durchmesser des zweiten Kreises ist gleich der Seite des zweiten Quadrats

6 Die Fläche des zweiten Kreises ist
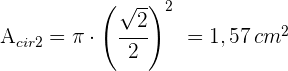
7 Somit ist die gesuchte Fläche
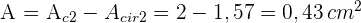
Der Umfang eines gleichschenkligen Trapezes misst 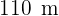 , die Grundseiten jeweils
, die Grundseiten jeweils  und
und 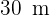 . Berechne die nicht parallelen Seiten und den Flächeninhalt.
. Berechne die nicht parallelen Seiten und den Flächeninhalt.
1 Wir stellen das Problem grafisch dar
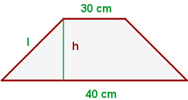
2 Da die Grundseiten addiert 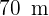 messen, ergibt sich für die Seiten
messen, ergibt sich für die Seiten 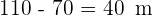 . Also misst jede Seite
. Also misst jede Seite 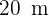 . Um die Höhe zu ermitteln, konstruieren wir ein rechtwinkliges Dreieck, wie in der Abbildung dargestellt. Nach dem Satz des Pythagoras ergibt sich
. Um die Höhe zu ermitteln, konstruieren wir ein rechtwinkliges Dreieck, wie in der Abbildung dargestellt. Nach dem Satz des Pythagoras ergibt sich
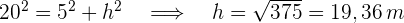
3 Wir berechnen den Flächeninhalt des Trapezes
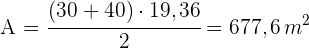
In ein regelmäßiges Sechseck mit der Seitenlänge 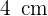 wird ein Kreis eingeschrieben und von einem weiteren Kreis umschrieben. Berechne den Flächeninhalt des so gebildeten Kreisrings.
wird ein Kreis eingeschrieben und von einem weiteren Kreis umschrieben. Berechne den Flächeninhalt des so gebildeten Kreisrings.
1 Wir stellen das Problem grafisch dar
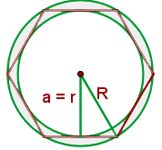
2 Wir berechnen den Radius des umschriebenen Kreises und stellen dazu fest, dass das Sechseck in sechs gleiche gleichseitige Dreiecke unterteilt ist, so dass
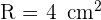
3 Wir berechnen den Radius des Inkreises, der mit der Höhe des gleichseitigen Dreiecks übereinstimmt
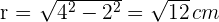
4 Wir berechnen die Fläche des Kreisrings. Diese ergibt sich aus der Differenz der Flächen der Kreise
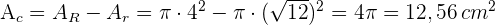
Auf einem Kreis befindet sich eine Sehne von 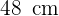 im Abstand von
im Abstand von 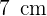 vom Mittelpunkt entfernt. Berechne den Flächeninhalt des Kreises.
vom Mittelpunkt entfernt. Berechne den Flächeninhalt des Kreises.
1 Wir stellen das Problem grafisch dar
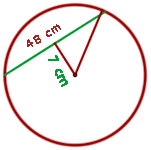
2 Wir betrachten das in der Abbildung dargestellte rechtwinklige Dreieck und berechnen mithilfe des Satzes des Pythagoras den Radius
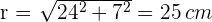
3 Wir berechnen die Fläche des Kreises
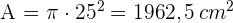
Die Katheten eines in einen Kreis eingeschriebenen, rechtwinkligen Dreiecks messen jeweils 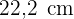 und
und 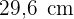 . Berechne die Länge des Kreisumfangs und den Flächeninhalt des Kreises.
. Berechne die Länge des Kreisumfangs und den Flächeninhalt des Kreises.
1 Wir stellen das Problem grafisch dar
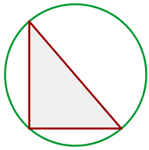
2 Die Hypotenuse fällt mit dem Durchmesser des Kreises zusammen. Mithilfe des Satzes des Pythagoras lässt sich der Radius berechnen
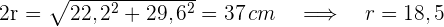
3 Wir berechnen die Länge des Kreisumfangs
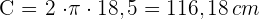
4 Wir berechnen den Flächeninhalt des Kreises
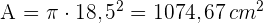
Auf einem Kreis mit einem Radius von 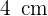 ist ein Kreiswinkel von
ist ein Kreiswinkel von  eingezeichnet. Berechne die Fläche des Kreissegments zwischen der Sehne, die die Enden der beiden Radien verbindet, und dem entsprechenden Bogen.
eingezeichnet. Berechne die Fläche des Kreissegments zwischen der Sehne, die die Enden der beiden Radien verbindet, und dem entsprechenden Bogen.
1 Wir stellen das Problem grafisch dar
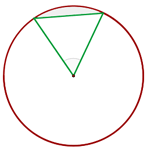
2 Die Fläche des Segments ist
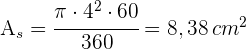
3 Um die Höhe des Dreiecks zu bestimmen, wenden wir den Satz des Pythagoras an
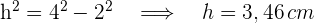
4 Wir berechnen den Flächeninhalt des gleichseitigen Dreiecks
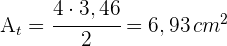
5 Die Fläche des Kreissegments ist
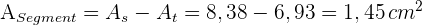
Mit KI zusammenfassen:


