Berechne die Fläche der Figur, die aus einem Quadrat und einem gleichseitigen Dreieck mit der Seitenlänge  besteht
besteht
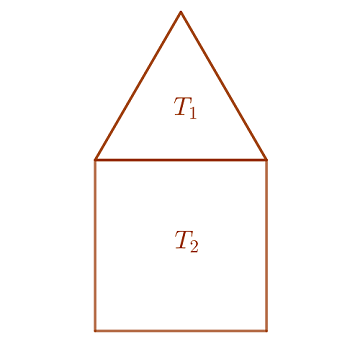
1 Wir berechnen die Fläche 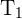 des Dreiecks. Da das Dreieck gleichseitig ist, teilt die Höhe es in 2 gleiche rechtwinklige Dreiecke. Unter Anwendung des Satzes des Pythagoras erhält man die Höhe
des Dreiecks. Da das Dreieck gleichseitig ist, teilt die Höhe es in 2 gleiche rechtwinklige Dreiecke. Unter Anwendung des Satzes des Pythagoras erhält man die Höhe
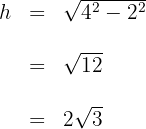
Die Fläche des gleichseitigen Dreiecks ist also gleich der Hälfte des Produkts aus Basis und Höhe
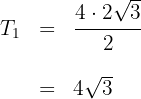
2 Wir berechnen die Fläche 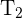 des Quadrats. Da eine Seite des Quadrats mit einer Seite des gleichseitigen Dreiecks übereinstimmt, hat das Quadrat die Seitenlänge
des Quadrats. Da eine Seite des Quadrats mit einer Seite des gleichseitigen Dreiecks übereinstimmt, hat das Quadrat die Seitenlänge  . Der Flächeninhalt eines Quadrats ist gleich dem Quadrat einer seiner Seiten
. Der Flächeninhalt eines Quadrats ist gleich dem Quadrat einer seiner Seiten
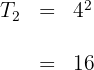
3 Die gesuchte Fläche ist gleich der Summe der Flächen des Dreiecks und des Quadrats
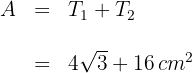
Berechne den Flächeninhalt des regelmäßiges Sechsecks mit der Seitenlänge  und dem Apothema
und dem Apothema 
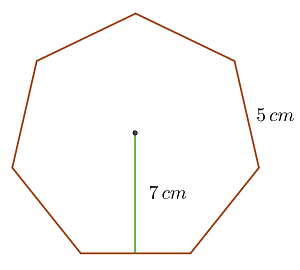
1 Um die Fläche zu berechnen, verwenden wir die Formel für regelmäßige Vielecke, die gleich der Hälfte des Produkts aus Umfang und Apothema ist

2 Wir berechnen den Umfang

3 Die gesuchte Fläche ist
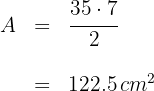
Berechne den Flächeninhalt des regelmäßigen Vielecks mit der Seitenlänge  und einem Abstand vom Mittelpunkt bis zu einem seiner Eckpunkte von
und einem Abstand vom Mittelpunkt bis zu einem seiner Eckpunkte von 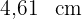
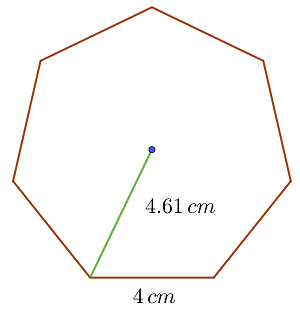
1 Um den Flächeninhalt zu berechnen, verwenden wir die Formel für regelmäßige Vielecke, die der Hälfte des Produkts aus Umfang und Apothema entspricht

2 Wir berechnen den Umfang
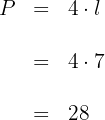
3 Da wir das Apothema nicht haben, ziehen wir ein Hilfssegment vom Mittelpunkt zum Mittelpunkt einer seiner Seiten und erhalten ein rechtwinkliges Dreieck, dessen Höhe gleich dem Apothema ist
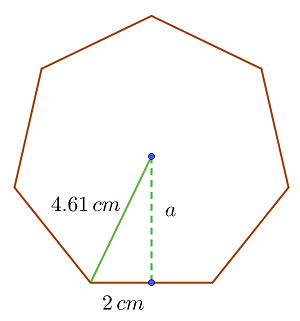
Wir berechnen das Apothema unter Verwendung des Satzes des Pythagoras
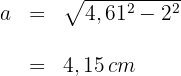
4 Die gesuchte Fläche ist
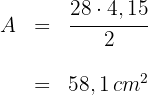
Berechne den Flächeninhalt des Quadrats, dessen Diagonale  misst
misst
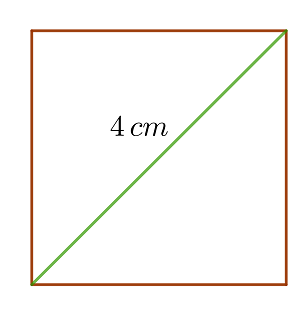
1 Um die Fläche zu berechnen, kann man sich das Quadrat als Raute vorstellen, deren zwei Diagonalen gleich sind
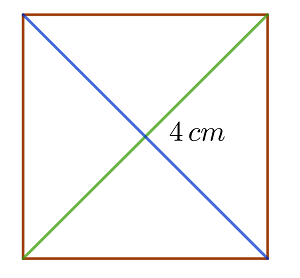
2 Die Fläche ist gleich der Hälfte des Produkts der Diagonalen
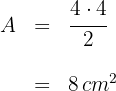
Berechne den Flächeninhalt des Trapezes, das durch Hinzufügen zweier gleichseitiger Dreiecke zum regelmäßigen Sechseck mit einer Seitenlänge von  und einem Apothema von
und einem Apothema von 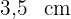 wird
wird
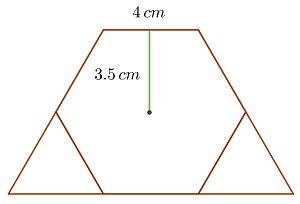
1 Um die Fläche zu berechnen, verwenden wir die Formel für das Trapez, die der Hälfte des Produkts aus der Summe der Basen mal der Höhe entspricht

2 Die größere Basis entspricht dem Dreifachen der Seitenlänge des Sechsecks, also 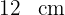 . Die kleinere Basis ist gleich
. Die kleinere Basis ist gleich  und die Höhe entspricht dem Apothema mal zwei, also
und die Höhe entspricht dem Apothema mal zwei, also  .
.
3 Die gesuchte Fläche ist
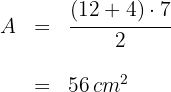
Berechne den Flächeninhalt eines Parallelogramms mit der Basis  und der Höhe
und der Höhe 
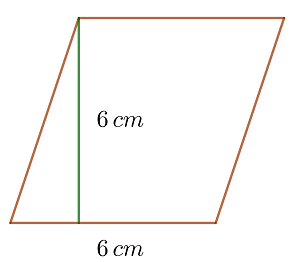
1 Um die Fläche zu berechnen, wenden wir die Formel des Parallelogramms an, die gleich dem Produkt aus Basis und Höhe ist
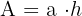
2 Die gesuchte Fläche ist
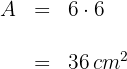
Berechne den Flächeninhalt des folgenden Vierecks, dessen Diagonalen  messen und senkrecht zueinander stehen
messen und senkrecht zueinander stehen
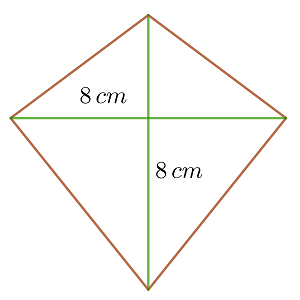
1 Da die Diagonalen des Vierecks senkrecht zueinander stehen, ist die Fläche gleich der Hälfte des Produkts der Diagonalen
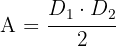
2 Die gesuchte Fläche ist
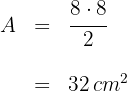
Berechne den Flächeninhalt der Figur, die aus einem Quadrat mit der Seitenlänge  und zwei gleichen Dreiecken gebildet wird, deren Abstand zwischen zwei ihrer Eckpunkte
und zwei gleichen Dreiecken gebildet wird, deren Abstand zwischen zwei ihrer Eckpunkte 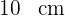 beträgt
beträgt
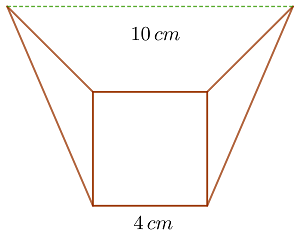
1Wir berechnen den Flächeninhalt 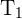 eines der Dreiecke. Wenn wir die Seite des Quadrats als Basis betrachten, dann ist die Höhe der beiden Dreiecke plus eine Seite des Quadrats gleich
eines der Dreiecke. Wenn wir die Seite des Quadrats als Basis betrachten, dann ist die Höhe der beiden Dreiecke plus eine Seite des Quadrats gleich 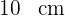 ; Die Höhe eines jeden Dreiecks ist somit
; Die Höhe eines jeden Dreiecks ist somit 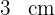
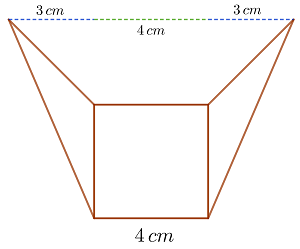
Dann ist der Flächeninhalt des Dreiecks gleich der Hälfte des Produkts aus Basis und Höhe
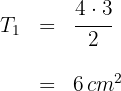
2 Wir berechnen den Flächeninhalt 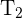 des Quadrats, der gleich dem Quadrat einer seiner Seiten ist
des Quadrats, der gleich dem Quadrat einer seiner Seiten ist

3 Die gesuchte Fläche ist gleich der Summe der Flächen der beiden Dreiecke und des Quadrats

Berechne den Flächeninhalt der Figur, die aus einem regelmäßigen Sechseck mit dem Flächeninhalt  und sechs gleichen gleichseitigen Dreiecken auf jeder Seite des Sechsecks besteht
und sechs gleichen gleichseitigen Dreiecken auf jeder Seite des Sechsecks besteht
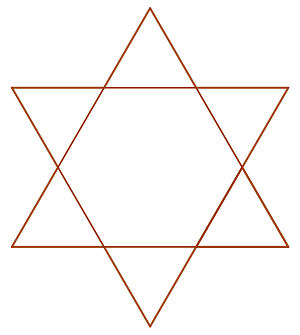
1 Da die Fläche des Sechsecks bekannt ist, muss nur noch die Fläche eines gleichseitigen Dreiecks ermittelt werden
2 Wir unterteilen das Sechseck in Dreiecke
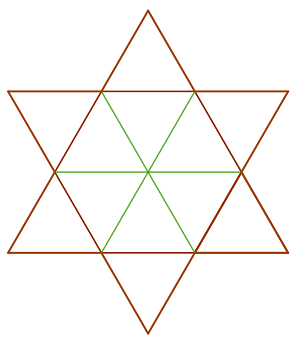
Wir stellen fest, dass das Sechseck in sechs gleiche gleichseitige Dreiecke unterteilt ist, die mit den äußeren gleichseitigen Dreiecken zusammenfallen, da sie eine gemeinsame Seite haben
3 Die gesuchte Fläche ist gleich der doppelten Fläche des Sechsecks
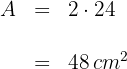
Berechne den Flächeninhalt der folgenden Figur, bei der die Seitenlänge des Quadrats  beträgt und die Höhe jedes Dreiecks gleich
beträgt und die Höhe jedes Dreiecks gleich  der Seitenlänge des Quadrats ist
der Seitenlänge des Quadrats ist
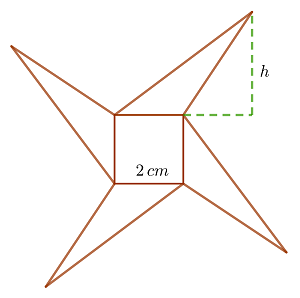
1 Der Flächeninhalt 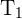 des Quadrats ist gleich dem Quadrat seiner Seiten
des Quadrats ist gleich dem Quadrat seiner Seiten

2 Die Höhe jeder Seite ist gleich  der Seitenlänge des Quadrats
der Seitenlänge des Quadrats
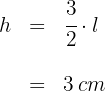
3 Der Flächeninhalt 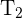 des Dreiecks ist gleich der Hälfte des Produkts aus Basis und Höhe
des Dreiecks ist gleich der Hälfte des Produkts aus Basis und Höhe
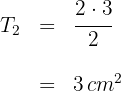
4 El área solicitada es
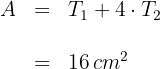
Mit KI zusammenfassen:


