Kapitel
Umfang und Fläche der Raute
Eine Raute ist ein Parallelogramm mit vier gleichen Seiten, dessen Winkel nicht rechtwinklig sind.
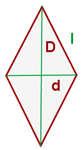
Der Umfang einer Raute ist gleich der Summe ihrer Seiten; da diese gleich sind, ergibt sich
Die Fläche einer Raute ist gleich der Hälfte des Produkts der Diagonalen:
Beispiel: Berechne den Umfang und die Fläche der Raute mit einer Seitenlänge von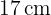 
den Diagonalen der Länge 
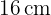und 
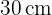
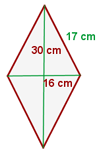
Wir berechnen den Umfang
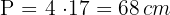
Wir berechnen die Fläche
Umfang und Fläche eines Rhomboids
Ein Rhomboid oder Parallelogramm mit gleichen gegenüberliegenden Seiten und nicht rechten Winkeln.
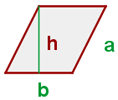
Der Umfang eines Rhomboids ist gleich der Summe seiner Seiten, d. h.
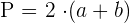
Der Flächeninhalt eines Rhomboids ist gleich dem Produkt aus seiner Grundfläche und seiner Höhe:
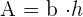
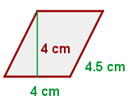
Beispiel: Berechne den Umfang und die Fläche des Rhomboids mit einer Seitenlänge von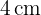 
und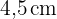 
sowie einer Höhe von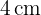
Wir berechnen den Umfang
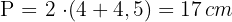
Wir berechnen die Fläche
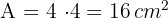
Aufgaben zu Rauten und Rhomboiden
Berechne den Flächeninhalt einer Raute, deren Hauptdiagonale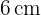 
und deren Nebendiagonale 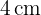ist.
1 Wir stellen die Raute grafisch dar
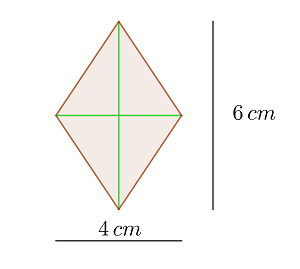
2 Wir wenden die Formel für den Flächeninhalt einer Raute an
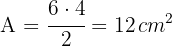
Somit beträgt die Fläche der Raute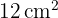 
Berechne den Flächeninhalt eines Rhomboids, dessen Grundseite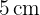 
und seine Höhte 
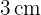misst.
1 Wir stellen den Rhomboid grafisch dar
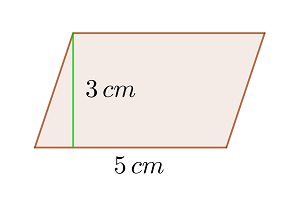
2 Wir wenden die Formel für die Fläche des Rhomboids an
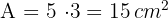
Somit beträgt der Flächeninhalt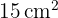 
Berechne die Fläche einer Raute, deren kürzere Diagonale 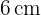und ihre Seite 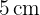misst
1 Wir stellen die Raute grafisch dar
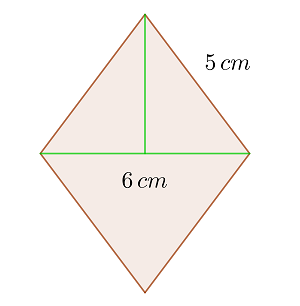
2 Wir müssen die längere Diagonale ermitteln. Da die Diagonalen einer Raute senkrecht stehen und sich in ihren Mittelpunkten schneiden, werden vier gleiche rechtwinklige Dreiecke gebildet, deren Schenkel der Hälfte der Diagonalen entsprechen. Wir wenden den Satz des Pythagoras an
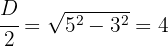
Die längere Diagonale misst somit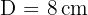 
3 Wir berechnen den Flächeninhalt
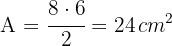
Berechne den Flächeninhalt eines Rhomboids mit den Eckpunkten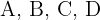 
sowie den Seiten 
und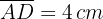 
. Wenn 
sich auf 
befindet, so dass 
senkrecht zu und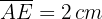 
ist. Berechne seinen Flächeninhalt.
span class="sa">1 Wir stellen den Rhomboid grafisch dar
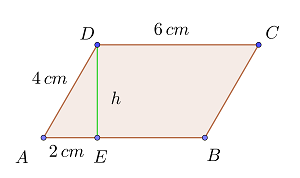
2 Wir müssen die Höhe berechnen. Das Dreieck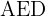 
ist rechtwinklig. Wir wenden des Satz des Pythagoras an.
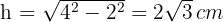
3 Wir berechnen die Fläche des Rhomboids
Berechne den Umfang einer Raute, deren Flächeninhalt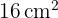 
ist und deren längere Diagonale 
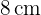misst
1 Wir stellen die Raute grafisch dar
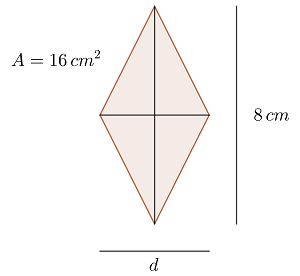
2 Anhand der Fläche der Raute berechnen dir die kürzere Diagonale
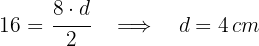
3 Wir müssen eine Seite berechnen. Da die Diagonalen einer Raute senkrecht aufeinander stehen und sich in ihren Mittelpunkten schneiden, entstehen vier gleiche rechtwinklige Dreiecke, deren Schenkel der Hälfte der Diagonalen entsprechen. Wir wenden den Satz des Pythagoras an
Somit misst die Seite 
4 Wir berechnen den Umfang
Berechne den Umfang eines Rhomboids, dessen Flächeninhalt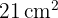 
ist. Seine Höhe ist 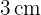und eine Seite, die nicht die Grundseite ist, misst 
.
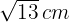1 Wir stellen den Rhomboid grafisch dar
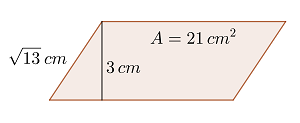
2 Wir müssen die Grundseite 
ermitteln. Wenn wir den Flächeninhalt und die Höhe des Rhomboids kennen, können wir seine Grundseite berechnen
3 Wir berechnen den Umfang
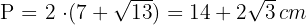
Der Umfang einer Raute beträgt 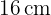und einer ihrer Winkel misst 
. Berechne den Flächeninhalt der Raute.
1 Wir stellen die Raute grafisch dar
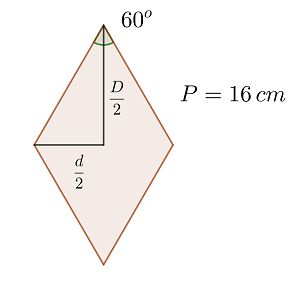
2 Aus dem Umfang der Raute berechnen wir die Seite der Raute
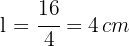
3 Da die Diagonalen einer Raute senkrecht aufeinander stehen, die Winkel halbieren und sich in ihren Mittelpunkten schneiden, entstehen vier gleiche rechtwinklige Dreiecke, deren Schenkel der Hälfte der Diagonalen entsprechen und deren Hypotenuse gleich der Seite ist. Wir wenden dis Sinus- und Kosinusfunktion an und erhalten
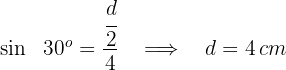
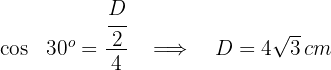
4 Wir berechnen den Flächeninhalt
Der Umfang eines Rhomboids ist 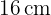, eine seiner Seiten ist ein Drittel seiner Grundseite und einer seiner Innenwinkel ist . Berechne den Flächeninhalt des Rhomboids
1 Wir stellen den Rhomboid grafisch darf
2 Aus dem Umfang berechnen wir die Seiten des Rhomboids
die Grundseite misst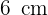 
und die andere Seite 
3 Die Höhe steht senkrecht zur Grundseite und bildet ein rechtwinkliges Dreieck wie in der Abbildung, wobei die Höhe der Schenkel ist, der dem Winkel von gegenüberliegt, und die Hypotenuse die Seite mit dem Maß . Wir wenden die Sinusfunktion an und erhalten
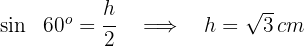
4 Wir berechnen den Flächeninhalt
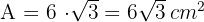
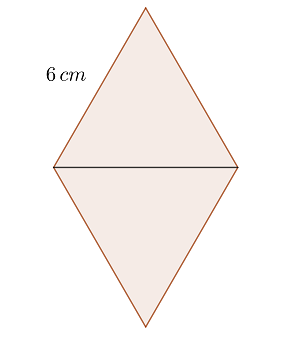
Zwei gleichseitige Dreiecke mit der Seitenlänge 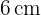werden zu einer Raute zusammengefügt. Berechne den Flächeninhalt der Raute.
1 Wir stellen die Raute grafisch dar
2 Um den Flächeninhalt der Raute zu berechnen, genügt es, den Flächeninhalt eines jeden gleichseitigen Dreiecks zu berechnen. Nach der Formel für den Flächeninhalt eines gleichseitigen Dreiecks erhält man
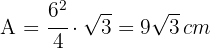
3 Der Flächeninhalt ist
Ein Rhomboid mit den Seiten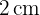 
und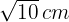 
hat eine Diagonale von 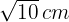, so dass man zwei gleichschenklige Dreiecke hat. Berechne den Flächeninhalt des Rhomboids.
1 Wir stellen den Rhomboid grafisch dar
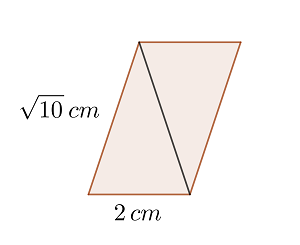
2 Um den Flächeninhalt des Rhomboids zu berechnen, braucht man nur die Höhe zu berechnen, die mit der Höhe des gleichschenkligen Dreiecks übereinstimmt. Wir wenden den Satz des Pythagoras an und erhalten
3 Der Flächeninhalt ist
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
