
Aussage des Satzes von Pythagoras
Der Satz des Pythagoras besagt Folgendes:
In allen rechtwinkligen Dreiecken ist die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates.
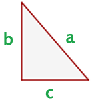
Aus der vorherigen Aussage können wir die folgende Formel ableiten, mit der wir den Betrag jeder der Seiten eines rechtwinkligen Dreiecks berechnen können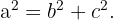
Anwendungen des Satzes von Pythagoras
Berechne die Hypotenuse.
1 Du kennst bereits die beiden Katheten, daher kannst du die Hypotenuse berechnen. Du musst nur die Variable  aus der Gleichung entfernen
aus der Gleichung entfernen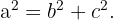
Dies machst du, indem du einfach die Quadratwurzel ziehst
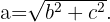
Beispiel: Die Katheten eines rechtwinkligen Dreiecks messen jeweils  und
und  . Wie lang ist die Hypotenuse?
. Wie lang ist die Hypotenuse?
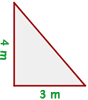
In diesem Fall hast du 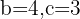 und musst den Wert von
und musst den Wert von  herausfinden.
herausfinden.
In die obige Formel einsetzen
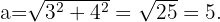
Die Hypotenuse misst also 
Eine Kathete berechnen.
2 Wenn du die Hypotenuse und eine Seite kennst, kannst du die andere Seite berechnen.
Aus deiner Ausgangsgleichung 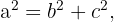 kannst du den Wert einer der Katheten eliminieren und erhältst für die Kathete
kannst du den Wert einer der Katheten eliminieren und erhältst für die Kathete 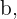
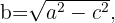
und für die Kathete 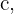

Beispiel: Die Hypotenuse eines rechtwinkligen Dreiecks ist 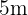 und einer der Katheten ist
und einer der Katheten ist  lang. Wie lang ist die andere Kathete?
lang. Wie lang ist die andere Kathete?
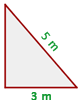
Laut der Abbildung misst die Kathete 
 , die Hypotenuse
, die Hypotenuse  und du musst die Kathete
und du musst die Kathete  finden. Verwende also die Formel zur Berechnung der Kathete,
finden. Verwende also die Formel zur Berechnung der Kathete,

Daher misst die Kathete 
 .
.
Klassifikation von rechtwinkligen Dreiecken.
3 Wenn du die Seiten eines Dreiecks kennst, kannst du herausfinden, ob es ein rechtwinkliges Dreieck ist oder nicht.
Damit ein Dreieck ein rechtwinkliges Dreieck ist, muss das Quadrat der größeren Seite gleich der Summe der Quadrate der beiden kleineren Seiten sein.
Beispiel: Bestimme, ob das folgende Dreieck ein rechtwinkliges Dreieck ist.
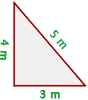
Beachte, dass die längste Seite dieses Dreiecks die Länge  hat. Wenn du mit der vorherigen Angabe fortfährst, musst du die folgenden Gleichungen überprüfen
hat. Wenn du mit der vorherigen Angabe fortfährst, musst du die folgenden Gleichungen überprüfen
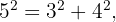
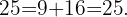
Da du auf beiden Seiten der Gleichheit das gleiche Ergebnis erhältst, kannst du darauf schließen, dass das Dreieck rechtwinklig ist.
Aufgaben
Eine 10 m lange Leiter ist an eine Wand gelehnt. Der Fuß der Leiter ist 6 m von der Wand entfernt. Welche Höhe erreicht die Leiter über der Wand?
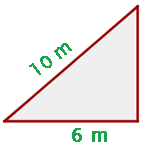
Die Treppe, die Wand und der Boden bilden ein rechtwinkliges Dreieck, bei dem du als Hypotenuse die Länge der Treppe und als einen der Schenkel die Länge vom Fuß der Treppe bis zur Wand nehmen kannst. Dann ist  und
und  Unser Ziel ist es dann, die Höhe der Treppe über der Wand zu berechnen, also die verbleibende Kathete zu berechnen. Nach unseren vorherigen Formeln und der Abbildung haben wir, dass
Unser Ziel ist es dann, die Höhe der Treppe über der Wand zu berechnen, also die verbleibende Kathete zu berechnen. Nach unseren vorherigen Formeln und der Abbildung haben wir, dass  .
.
Finde den Flächeninhalt des gleichseitigen Dreiecks:
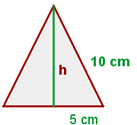
Zuerst zeichnest du die Höhe des gleichseitigen Dreiecks ein. Diese Höhe teilt das Dreieck in zwei rechtwinklige Dreiecke mit den Katheten  , der Höhe des gleichseitigen Dreiecks,
, der Höhe des gleichseitigen Dreiecks,  , der Hälfte einer der Seiten des Dreiecks und schließlich mit der Hypotenuse
, der Hälfte einer der Seiten des Dreiecks und schließlich mit der Hypotenuse  , einer der Seiten des Ausgangsdreiecks. Auf diese Weise musst du zur Höhenberechnung nur die vorherige Formel für das Finden von Katheten rechtwinkliger Dreiecke anwenden, die uns ergibt
, einer der Seiten des Ausgangsdreiecks. Auf diese Weise musst du zur Höhenberechnung nur die vorherige Formel für das Finden von Katheten rechtwinkliger Dreiecke anwenden, die uns ergibt 

Der Flächeninhalt eines Dreiecks ergibt sich aus der Formel 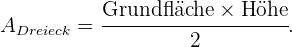 Du stellst fest, dass die Grundseite des Dreiecks
Du stellst fest, dass die Grundseite des Dreiecks 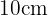 und die Höhe
und die Höhe 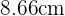 beträgt. Dann ergibt sich durch Einsetzen in die Flächenformel
beträgt. Dann ergibt sich durch Einsetzen in die Flächenformel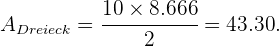
Finde die Diagonale des Quadrats:
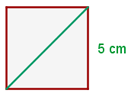
Die Diagonale des Quadrats, dessen Seiten 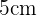 messen, teilt die genannte Figur in zwei rechtwinklige Dreiecke, wobei die Diagonale
messen, teilt die genannte Figur in zwei rechtwinklige Dreiecke, wobei die Diagonale  mit der Hypotenuse eines dieser Dreiecke zusammenfällt. Das heißt, du musst die Hypotenuse eines rechtwinkligen Dreiecks finden, dessen Katheten gleich
mit der Hypotenuse eines dieser Dreiecke zusammenfällt. Das heißt, du musst die Hypotenuse eines rechtwinkligen Dreiecks finden, dessen Katheten gleich 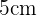 sind.
sind.
Verwende dazu verwendest die Formel für die Hypotenuse:

Die Diagonale beträgt also 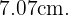
Finde die Diagonale des Rechtecks:
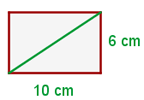
Ähnlich wie in der vorherigen Übung teilt die Diagonale  dieses Rechtecks in zwei rechtwinklige Dreiecke von
dieses Rechtecks in zwei rechtwinklige Dreiecke von 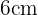 und
und 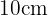 und die Diagonale fällt mit der Hypotenuse dieser Dreiecke zusammen. Also musst du wieder die Formel verwenden, um die Hypotenuse zu berechnen:
und die Diagonale fällt mit der Hypotenuse dieser Dreiecke zusammen. Also musst du wieder die Formel verwenden, um die Hypotenuse zu berechnen: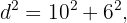
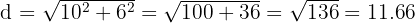
Die Länge der Diagonale beträgt daher 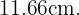
Finde den Umfang und die Fläche des rechtwinkligen Trapezes:
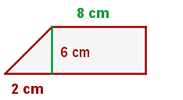
Der Umfang des Trapezes ist die Summe der Längen seiner Seiten. Aus der Abbildung geht hervor, dass die Oberseite des Trapezes 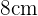 , die Unterseite
, die Unterseite 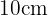 und die Höhe des Trapezes
und die Höhe des Trapezes 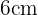 misst. Um die diagonale Seite des Trapezes zu finden, die du
misst. Um die diagonale Seite des Trapezes zu finden, die du  nennst, musst du das rechtwinklige Dreieck mit der senkrechten Seite
nennst, musst du das rechtwinklige Dreieck mit der senkrechten Seite 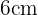 , der waagerechten Seite
, der waagerechten Seite 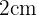 und der Hypotenuse
und der Hypotenuse  betrachten. Da du den Wert von
betrachten. Da du den Wert von 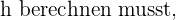 verwendest du die Formel zur Berechnung der Hypotenuse:
verwendest du die Formel zur Berechnung der Hypotenuse: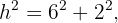
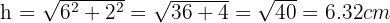
Am Schluss kannst du den Umfang berechnen, der dasselbe wie die Summe ist: 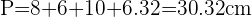 . Um die Fläche zu berechnen musst du wissen, dass das Trapez aus einem rechtwinkligen Dreieck und einem Rechteck besteht. Daher musst du nur die beiden Flächen zusammenrechnen. Das bedeutet
. Um die Fläche zu berechnen musst du wissen, dass das Trapez aus einem rechtwinkligen Dreieck und einem Rechteck besteht. Daher musst du nur die beiden Flächen zusammenrechnen. Das bedeutet 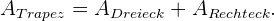 Der Flächeninhalt des Rechtecks ist das Produkt aus seiner Grundseite und seiner Höhe, also
Der Flächeninhalt des Rechtecks ist das Produkt aus seiner Grundseite und seiner Höhe, also 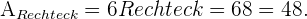 Für den Flächeninhalt des Dreiecks gilt
Für den Flächeninhalt des Dreiecks gilt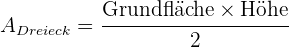
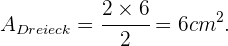 Daher
Daher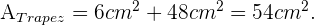
Der Umfang eines gleichschenkligen Trapezes beträgt 110 m, die Grundseiten messen 40 m bzw. 30 m. Berechne die nicht-parallelen Seiten und den Flächeninhalt.
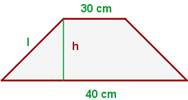
Der Umfang des Trapezes ist gleich der Summe der Längen seiner Seiten. Dann hast du die folgende Gleichheit 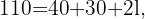 , wobei
, wobei  der Wert der nicht-parallelen Seite ist. Wenn du
der Wert der nicht-parallelen Seite ist. Wenn du  aus der vorherigen Gleichung entfernst, weißt du, dass
aus der vorherigen Gleichung entfernst, weißt du, dass 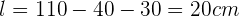 ist. Auf diese Weise hast du bereits den ersten Teil des Problems gelöst. Erinnere dich daran, dass die Fläche des Trapezes gleich der Summe der Grundseite ist, multipliziert mit der Höhe und diese dann durch zwei geteilt wird. Du musst also die Höhe des Trapezes berechnen, die du
ist. Auf diese Weise hast du bereits den ersten Teil des Problems gelöst. Erinnere dich daran, dass die Fläche des Trapezes gleich der Summe der Grundseite ist, multipliziert mit der Höhe und diese dann durch zwei geteilt wird. Du musst also die Höhe des Trapezes berechnen, die du  nennst. Aus der Abbildung kannst du das rechtwinklige Dreieck mit den Katheten
nennst. Aus der Abbildung kannst du das rechtwinklige Dreieck mit den Katheten 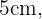
 und der Hypotenuse
und der Hypotenuse  betrachten. Um den Wert von
betrachten. Um den Wert von  zu finden, verwendest du anschließend die Formel zur Berechnung der Katheten,
zu finden, verwendest du anschließend die Formel zur Berechnung der Katheten,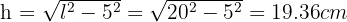 Nun kannst du den Flächeninhalt des Trapezes berechnen,
Nun kannst du den Flächeninhalt des Trapezes berechnen,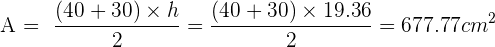
Finde den Flächeninhalt eines regelmäßigen Fünfecks:
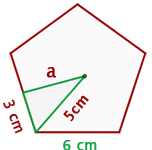
Du weißt, dass die Seiten des regelmäßigen Fünfecks 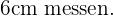 Da der Flächeninhalt des Fünfecks gleich der Hälfte des Umfangs mal dem Wert des Apothemas ist, musst du den Wert des Apothemas finden. Du nennst das Apothema
Da der Flächeninhalt des Fünfecks gleich der Hälfte des Umfangs mal dem Wert des Apothemas ist, musst du den Wert des Apothemas finden. Du nennst das Apothema  , wie in der Abbildung dargestellt. Um
, wie in der Abbildung dargestellt. Um  zu berechnen, betrachtest du das Dreieck mit den Katheten
zu berechnen, betrachtest du das Dreieck mit den Katheten  ,
,  und der Hypotenuse
und der Hypotenuse 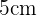 . Du verwendest also die Formel zur Berechnung der Katheten:
. Du verwendest also die Formel zur Berechnung der Katheten: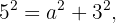
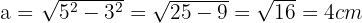
Der Wert des Umfangs des Fünfecks ist 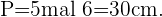 . Schließlich kannst du den Flächeninhalt des Fünfecks berechnen.
. Schließlich kannst du den Flächeninhalt des Fünfecks berechnen. 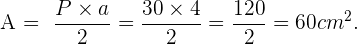
Berechne den Flächeninhalt des eingeschriebenen Quadrats von einem Umkreis mit einer Länge von 18.84 m.
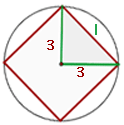
Da das Quadrat in einen Kreis eingeschrieben ist, kannst du es in  rechtwinklige Dreiecke mit Katheten gleich dem Radius des Kreises,
rechtwinklige Dreiecke mit Katheten gleich dem Radius des Kreises,  , und der Hypotenuse
, und der Hypotenuse  aufteilen und so die Seite des Dreiecks mit der Formel für die Berechnung von Hypotenusen berechnen,
aufteilen und so die Seite des Dreiecks mit der Formel für die Berechnung von Hypotenusen berechnen, 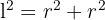
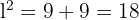 .
.
Da der Flächeninhalt des Quadrats also 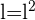 ist, folgt daraus, dass er gleich
ist, folgt daraus, dass er gleich  ist.
ist.
In einem Kreis misst ein Seil 48 cm und ist 7 cm vom Mittelpunkt entfernt. Berechne den Flächeninhalt des Kreises.
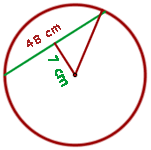
Um den Flächeninhalt des Kreises zu berechnen, musst du zunächst seinen Radius ermitteln. Da die Sehne des Kreises  vom Mittelpunkt entfernt ist, kannst du ein rechtwinkliges Dreieck mit den Katheten
vom Mittelpunkt entfernt ist, kannst du ein rechtwinkliges Dreieck mit den Katheten  , der halben Sehne,
, der halben Sehne, 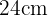 und der Hypotenuse gleich dem Radius des Kreises,
und der Hypotenuse gleich dem Radius des Kreises,  , bilden. Um den Radius zu finden, musst du also die Formel zur Berechnung von Hypotenusen verwenden.
, bilden. Um den Radius zu finden, musst du also die Formel zur Berechnung von Hypotenusen verwenden.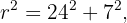
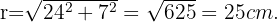
Así, el area del círculo es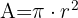

Mit KI zusammenfassen:













