Willkommen in unserem Abschnitt zum Thema Aufgaben zum Umfang und Kreis!
In dieser Reihe von Übungen werden wir die grundlegenden Eigenschaften und Konzepte im Zusammenhang mit dem Umfang und dem Kreis, zwei Schlüsselelementen der Geometrie, untersuchen. Diese geometrischen Figuren sind nicht nur für sich genommen wichtig, sondern haben auch praktische Anwendungen in einer Vielzahl von Bereichen, von der Physik bis zum Ingenieurwesen und darüber hinaus.
Durch diese Übungen kannst du Themen wie die Berechnung des Umfangs und der Fläche eines Kreises, die Beziehung zwischen Umfang und Durchmesser, die Verwendung grundlegender Formeln und das Lösen praktischer Probleme im Zusammenhang mit Umfang und Kreisen vertiefen.
Das Rad eines LKWs hat einen Radius von  cm. Wie weit ist der LKW gefahren, wenn sich das Rad
cm. Wie weit ist der LKW gefahren, wenn sich das Rad  Mal gedreht hat?
Mal gedreht hat?
Da der Radius des Rades 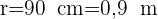 beträgt, ist sein Durchmesser
beträgt, ist sein Durchmesser 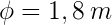 . Andererseits muss man bedenken, dass der Umfang die Länge des Kreises darstellt, was der Entfernung entspricht, die der Lkw bei einer Umdrehung zurücklegt. Daraus ergibt sich, dass der Umfang des Rades
. Andererseits muss man bedenken, dass der Umfang die Länge des Kreises darstellt, was der Entfernung entspricht, die der Lkw bei einer Umdrehung zurücklegt. Daraus ergibt sich, dass der Umfang des Rades 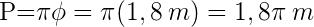 ist. Wenn wir also wissen wollen, welche Strecke der Lkw bei 100 Umrundungen zurückgelegt hat, dann:
ist. Wenn wir also wissen wollen, welche Strecke der Lkw bei 100 Umrundungen zurückgelegt hat, dann: 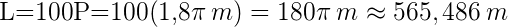 .
.
Ein Leuchtturm strahlt sein Licht in einem flachen Winkel von 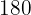 Grad. Wenn die maximale Reichweite des Leuchtturms
Grad. Wenn die maximale Reichweite des Leuchtturms  Meilen beträgt, wie groß ist dann die maximale Länge des entsprechenden Lichtstrahls in Metern?
Meilen beträgt, wie groß ist dann die maximale Länge des entsprechenden Lichtstrahls in Metern?
Wenn ein Kreisbogen der Länge  eines Kreises mit dem Radius
eines Kreises mit dem Radius  einen zentralen Winkel von
einen zentralen Winkel von  im Bogenmaß einschließt, dann ist
im Bogenmaß einschließt, dann ist 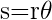 . Diese Formel wird zur Lösung des Problems verwendet, wir benötigen jedoch den Winkel im Bogenmaß, d. h.
. Diese Formel wird zur Lösung des Problems verwendet, wir benötigen jedoch den Winkel im Bogenmaß, d. h. 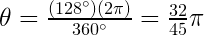 . Die Länge des Kreisbogens ist
. Die Länge des Kreisbogens ist 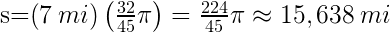 . Bei diesem Problem gehen wir davon aus, dass
. Bei diesem Problem gehen wir davon aus, dass 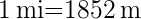 die in der See- und Luftschifffahrt verwendete Längeneinheit ist. Die Länge des Bogens in Metern ist somit:
die in der See- und Luftschifffahrt verwendete Längeneinheit ist. Die Länge des Bogens in Metern ist somit: 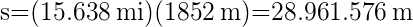
Die Länge des Umfangs eines Kreises ist 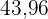 cm. Welchen Flächeninhalt hat der Kreis?
cm. Welchen Flächeninhalt hat der Kreis?
Die Länge des Umfangs entspricht dem Umfang des Kreises, der mit der folgenden Formel berechnet wird: 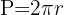 , wobei
, wobei  der Radius des Kreises ist. Wir können den Ausdruck wie folgt schreiben:
der Radius des Kreises ist. Wir können den Ausdruck wie folgt schreiben: 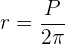 . Der Flächeninhalt des Kreises wird mit der folgenden Formel berechnet:
. Der Flächeninhalt des Kreises wird mit der folgenden Formel berechnet:  .
.
Wenn wir den vorher ermittelten Wert von  einsetzen, erhalten wir:
einsetzen, erhalten wir: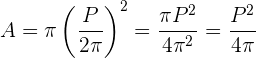 .
.
Betrachtet man schließlich den numerischen Wert von  , so ergibt sich der Flächeninhalt des Kreises wie folgt:
, so ergibt sich der Flächeninhalt des Kreises wie folgt:
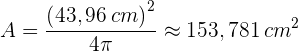
Die Fläche eines Kreissektors von  ist
ist 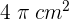 . Berechne den Radius des Kreises, zu dem er gehört, und die Länge des Kreisumfangs.
. Berechne den Radius des Kreises, zu dem er gehört, und die Länge des Kreisumfangs.
Die Formel zur Berechnung der Fläche eines Kreissektors lautet  , wobei
, wobei  die Anzahl der Grade und
die Anzahl der Grade und  der entsprechende Radius des Kreissektors ist. Daraus ergibt sich:
der entsprechende Radius des Kreissektors ist. Daraus ergibt sich: 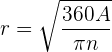 .
.
Setzen wir nun die Zahlenwerte der Aufgabe ein, so ergibt sich, dass der Radius des Kreises, zu dem der Kreissektor gehört, wie folgt lautet:  . Schließlich ist die Länge des Kreisumfangs
. Schließlich ist die Länge des Kreisumfangs 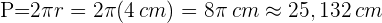
Berechne die Fläche eines Kreissektors, dessen Sehne die Seite des eingeschriebenen gleichseitigen Dreiecks ist, wobei  cm der Radius des Umfangs ist.
cm der Radius des Umfangs ist.
Die Formel zur Berechnung der Fläche eines Kreissektors lautet:  , wobei
, wobei  die Anzahl der Grade und
die Anzahl der Grade und  der Radius des Kreissektors ist. Da die Innenwinkel eines gleichseitigen Dreiecks alle
der Radius des Kreissektors ist. Da die Innenwinkel eines gleichseitigen Dreiecks alle  messen, und wenn man bedenkt, dass der Scheitelpunkt des zentralen Winkels des Bogens mit dem Mittelpunkt des Kreises zusammenfällt (siehe Abbildung), misst dieser Winkel
messen, und wenn man bedenkt, dass der Scheitelpunkt des zentralen Winkels des Bogens mit dem Mittelpunkt des Kreises zusammenfällt (siehe Abbildung), misst dieser Winkel 
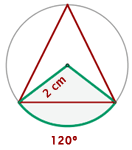
Die Fläche des Kreissektors ist: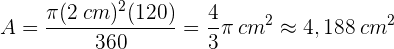
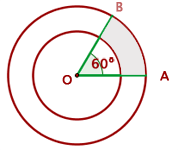
Gegeben sind zwei konzentrische Kreise mit den Radien  und
und 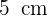 . Es werden die Radien
. Es werden die Radien 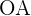 und
und  eingezeichnet, die einen Winkel von
eingezeichnet, die einen Winkel von 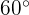 bilden. Berechne den Flächeninhalt des gebildeten kreisförmigen Trapezes.
bilden. Berechne den Flächeninhalt des gebildeten kreisförmigen Trapezes.
Die Fläche des gebildeten kreisförmigen Trapezes (siehe Abbildung) kann wie folgt berechnet werden:  , wobei
, wobei 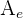 die Fläche des Kreissektors des äußeren Kreises (mit dem Radius
die Fläche des Kreissektors des äußeren Kreises (mit dem Radius 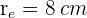 ) und
) und  die Fläche des Kreissektors des inneren Kreises (mit dem Radius
die Fläche des Kreissektors des inneren Kreises (mit dem Radius  ) ist.
) ist.
Somit: 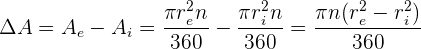
Anschließend setzen wir die Zahlenwerte in die Formel ein und erhalten die Fläche: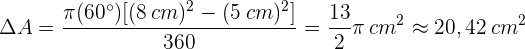
In einem kreisförmigen Park mit einem Radius von 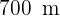 befindet sich in der Mitte ein ebenfalls kreisförmiger Springbrunnen mit einem Radius von
befindet sich in der Mitte ein ebenfalls kreisförmiger Springbrunnen mit einem Radius von 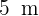 . Berechne die Fläche des Fußgängerbereichs.
. Berechne die Fläche des Fußgängerbereichs.
In der Abbildung ist der Bereich, der der Fußgängerzone entspricht, grau dargestellt. Diese Zone entspricht der Fläche, die von zwei konzentrischen Kreisen, d. h. einer kreisförmigen Krone, begrenzt wird. Die Fläche einer kreisförmigen Krone wird wie folgt berechnet:  , wobei
, wobei 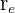 der größere Radius (äußerer Radius) und
der größere Radius (äußerer Radius) und 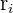 der kleinere Radius (innerer Radius) ist.
der kleinere Radius (innerer Radius) ist.

Aus den Angaben der Aufgabe ergibt sich nun: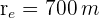
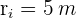
Daher ist die Fläche des Fußgängerbereichs im Park: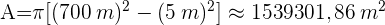
Die Oberfläche eines Tisches besteht aus einem quadratischen Mittelteil mit den Seiten 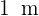 und zwei Halbkreisen, die an zwei gegenüberliegenden Seiten angebracht sind. Berechne Sie den Flächeninhalt.
und zwei Halbkreisen, die an zwei gegenüberliegenden Seiten angebracht sind. Berechne Sie den Flächeninhalt.
Da der mittlere Teil des Tisches ein Quadrat ist, sind die beiden seitlichen Halbkreise gleich und bilden einen einzigen Kreis mit dem Durchmesser 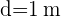 (siehe Abbildung).
(siehe Abbildung).

Der Flächeninhalt des Tischs ist:
 ist die Länge des Tisches
ist die Länge des Tisches ist der Durchmesser des Kreises
ist der Durchmesser des Kreises
Wir setzen die Werte ein und erhalten den Flächeninhalt des Tisches: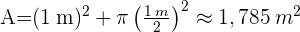
Berechne die Fläche des schattierten Teils, wenn der Radius des größeren Kreises 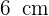 und der Radius der kleineren Kreise
und der Radius der kleineren Kreise 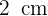 beträgt.
beträgt.
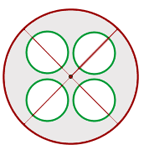
Gemäß der gegebenen geometrischen Figur wird die schattierte Fläche wie folgt berechnet: 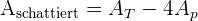 .
. 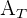 ist die Fläche des großen Kreises mit dem Radius
ist die Fläche des großen Kreises mit dem Radius 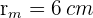 .
.  ist die Fläche jedes der kleinen Kreise mit dem Radius
ist die Fläche jedes der kleinen Kreise mit dem Radius 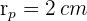 . Wir haben also
. Wir haben also 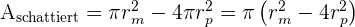 . Schließlich setzen wir die Werte ein und erhalten so die Fläche des schattierten Bereichs:
. Schließlich setzen wir die Werte ein und erhalten so die Fläche des schattierten Bereichs: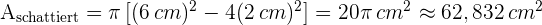
Berechne die Fläche der schattierten Fläche, wobei  ,
,  ein Quadrat ist und
ein Quadrat ist und 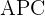 und
und  Kreisbögen mit den Mittelpunkten
Kreisbögen mit den Mittelpunkten  und
und  sind.
sind.
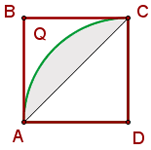
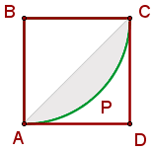
Da beide Kreissegmente gleich sind, können wir ohne Einschränkung der Allgemeingültigkeit jedes dieser Segmente analysieren. Beachte, dass jedes Kreissegment aus einem gleichschenkligen Dreieck und einem Kreissektor besteht, dessen Öffnung 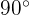 beträgt. Somit:
beträgt. Somit: 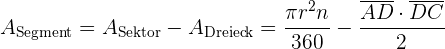 . Schließlich setzen wir die Werte in den obigen Ausdruck ein, und die Fläche 1 Kreissegments beträgt
. Schließlich setzen wir die Werte in den obigen Ausdruck ein, und die Fläche 1 Kreissegments beträgt 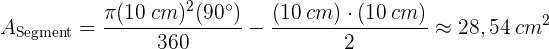 . Die gesuchte schattierte Fläche ist somit
. Die gesuchte schattierte Fläche ist somit 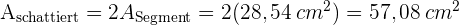
Ein Kommunikationssatellit umkreist die Erde in einem Winkel von 45° zum Äquator. Wenn die Höhe des Satelliten 10.000 km beträgt, wie lang ist dann die maximale Länge der Strecke in Kilometern, die er auf seiner Umlaufbahn zurücklegt?
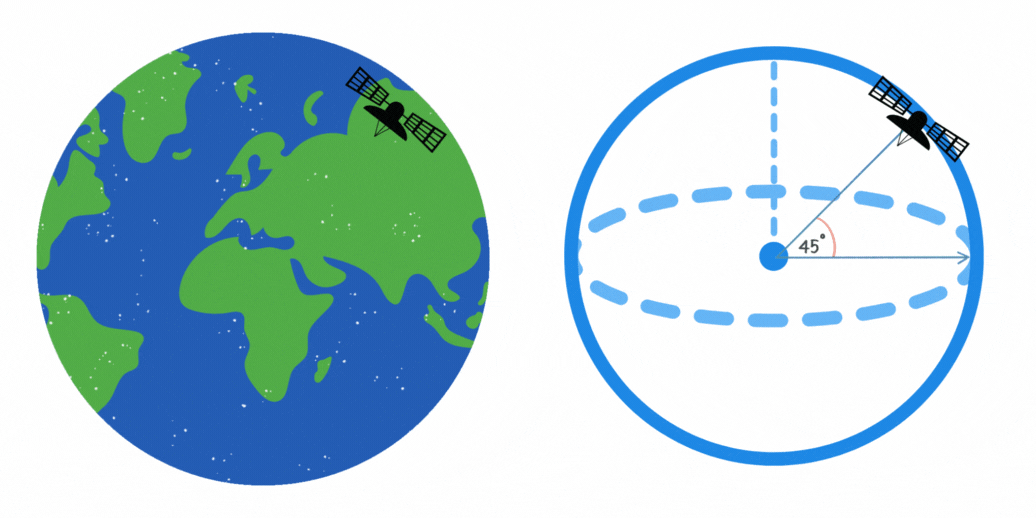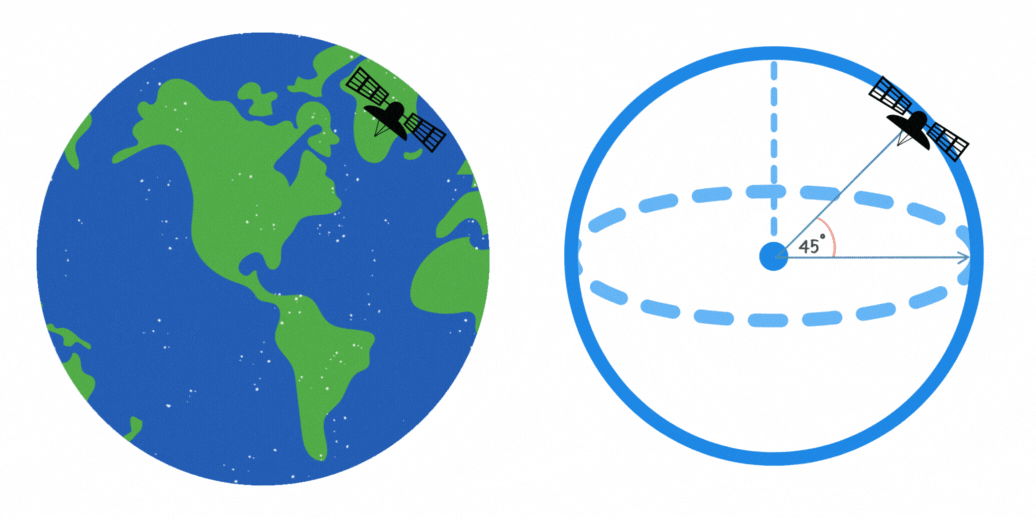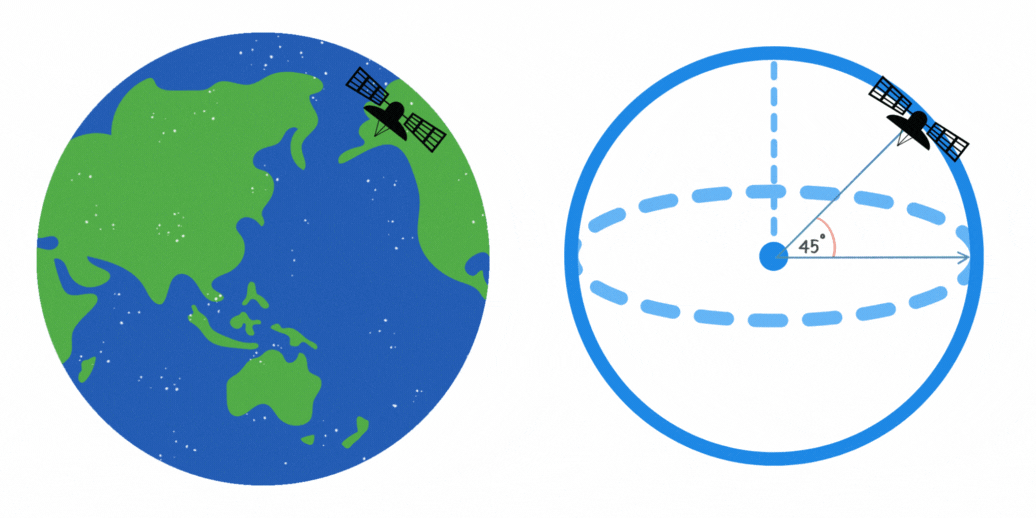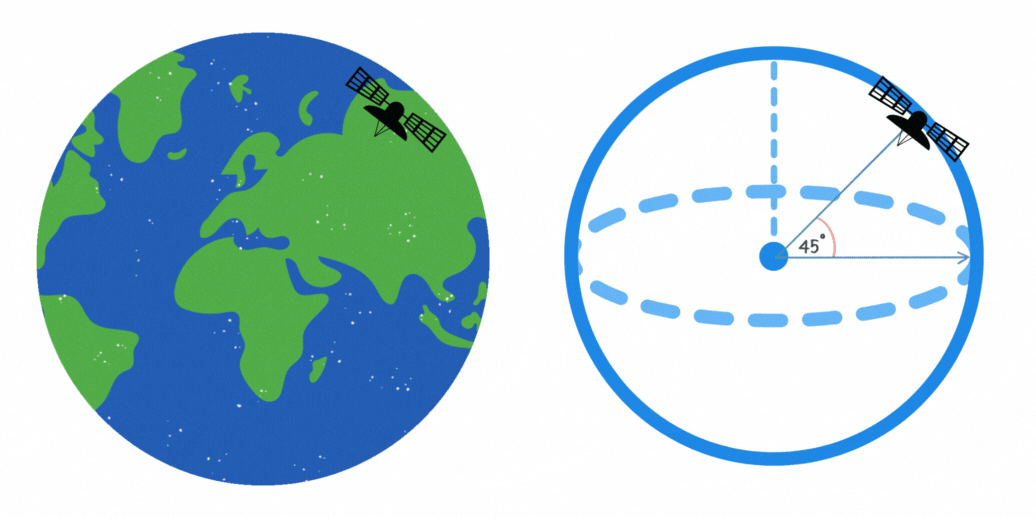
Die Länge der Strecke, die der Satellit auf seiner Umlaufbahn zurücklegt, kann mithilfe der Formel für einen Kreisbogen berechnet werden. Dies ist in der Abbildung zu sehen, da der Satellit einer kreisförmigen Bahn mit konstantem Radius folgt. Die Formel lautet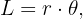 ,
,
wobei 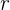 der Abstand zwischen Erdmittelpunkt und Satellit ist.
der Abstand zwischen Erdmittelpunkt und Satellit ist.  ist der Winkel im Bogenmaß. Wir beachten dass 45° dem Bogenmaß
ist der Winkel im Bogenmaß. Wir beachten dass 45° dem Bogenmaß 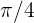 entspricht. Der Satellit legt also folgende Strecke zurück
entspricht. Der Satellit legt also folgende Strecke zurück
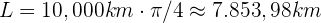
Ein Riesenrad hat einen Radius von 15 m. Wenn sich das Riesenrad dreimal dreht, welche Strecke hat ein Besucher auf dem Umfang des Rades zurückgelegt?
Die Strecke, die ein Besucher auf dem Riesenrad zurücklegt, kann anhand des Umfangs des Rades und der Anzahl der Umdrehungen berechnet werden. Das heißt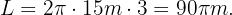
Ein Fahrrad mit Rädern von 26 cm Durchmesser legt 5 km zurück. Wie viele vollständige Umdrehungen hat jedes Rad auf dieser Strecke gemacht?
Wenn 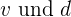 die zurückgelegten Runden bzw. der Durchmesser sind, kann die gesamte zurückgelegte Strecke wie folgt berechnet werden
die zurückgelegten Runden bzw. der Durchmesser sind, kann die gesamte zurückgelegte Strecke wie folgt berechnet werden
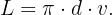
Da wir die gesamte zurückgelegte Strecke kennen, müssen wir nach 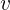 auflösen:
auflösen:
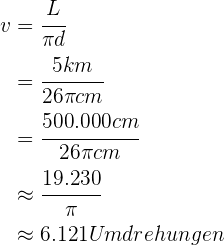
Eine kreisförmige Torte wird in 8 gleiche Stücke geschnitten. Wenn die Torte einen Radius von 20 cm hat, wie lang ist der Bogen jedes Stücks? Wie groß ist die Fläche der Oberseite der Torte?
Um den Winkel zu berechnen, teilen wir 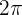 einfach in 8 Teile auf. Jedes Teilstück ist also
einfach in 8 Teile auf. Jedes Teilstück ist also
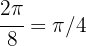
des kompletten Sektors. Da die Torte einen Radius von 20 cm hat, ist der Flächeninhalt dieses Sektors
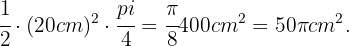
Welchen Radius muss ein Rad haben, um in 3 Umdrehungen eine vollständige Umdrehung um den Erdäquator zu unternehmen?
Zunächst berechnen wir die Entfernung des Äquators von der Erde: Wir wissen, dass der Radius zum Äquator 6.378 km beträgt. Wir müssen also folgende Strecke
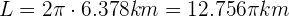
in 3 Umdrehungen zurücklegen. Der Radius , queremos que el radio 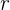 unseres Rades muss also
unseres Rades muss also  sein. Somit
sein. Somit
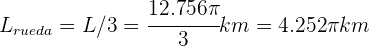
muss die Länge des Umfangs sein. Der Radius muss also wie folgt sein:
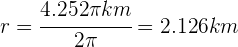
Mit KI zusammenfassen:



