Der Satz des Thales ist ein grundlegendes Konzept der Geometrie, das uns hilft, die Eigenschaften geometrischer Figuren und die Beziehungen zwischen ihren Elementen zu verstehen. Dieses Theorem stellt eine leistungsfähige Verbindung zwischen parallelen Geraden und ähnlichen Dreiecken her, und seine Anwendung erstreckt sich auf eine Vielzahl von geometrischen Problemen.
In den folgenden Übungen werden wir untersuchen, wie man den Satz des Thales anwenden kann, um praktische Probleme zu lösen und seine Eigenschaften in realen Situationen zu beweisen. Durch diese Übungen werden wir ein tieferes Verständnis für dieses wichtige Theorem und seine Bedeutung für die Lösung alltäglicher geometrischer Probleme entwickeln.
Los geht's mit der Erkundung der faszinierenden Welt von Thales!
Um den Satz des Thales anwenden zu können, brauchen wir...
Bitte wähle eine Antwort aus.
Eine der Anwendungen des Satzes des Thales ist...
Bitte wähle eine Antwort aus.
Wir können den Satz des Thales auf Dreiecke anwenden, wenn...
Bitte wähle eine Antwort aus.
Der Satz des Thales besagt, dass, wenn mehrere parallele Geraden durch zwei Sekanten geschnitten werden, die entsprechenden Segmente, die durch die Sekanten bestimmt sind,...
Bitte wähle eine Antwort aus.
Zwei Dreiecke erfüllen den Satz des Thales, wenn...
Bitte wähle eine Antwort aus.
Wenn zwei Dreiecke parallele Seiten haben, dann sind nach dem Satz des Thales die beiden Dreiecke...
Bitte wähle eine Antwort aus.
Nach dem Satz des Thales sind zwei rechtwinklige Dreiecke ähnlich, wenn....
Bitte wähle eine Antwort aus.
Wenn die Geraden 
, 
und 
parallel sind, ist die Länge von 
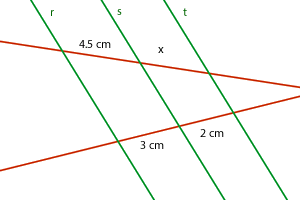
Bitte wähle eine Antwort aus.
Da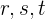 
parallel sind, kann der Satz des Thales angewendet werden:
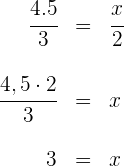
Die Geraden , und sind parallel. Die fehlenden Längen sind:
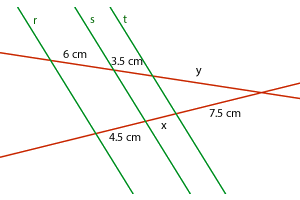
Bitte wähle eine Antwort aus.
Da parallel sind, haben wir die Bedingungen des Satzes des Thales, so dass wir ihn anwenden können:
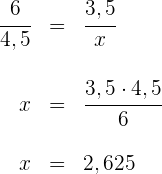
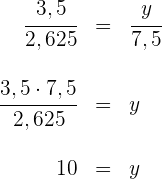
und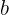 
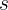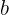sind zwei beliebige Geraden und sowie sind zwei Geraden, die sie schneiden. Wenn die Segmente, die und bestimmen, 
, 
, 
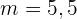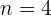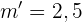und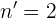 
sind, gilt...
Bitte wähle eine Antwort aus.
Wir prüfen, ob der Satz des Thales erfüllt ist: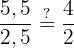
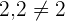
Der Satz des Thales kann nicht angewendet werden, da die Geraden und 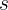nicht parallel sind.
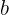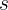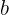Gegeben sind die beliebigen Geraden und sowie die Geraden und , die sie schneiden. Wenn die Segmente, die und bestimmen, 
, 
, 
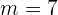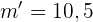und 
sind, dann...
Bitte wähle eine Antwort aus.
Wir überprüfen, ob der Satz des Thales erfüllt ist:
Der Satz des Thales kann angewendet werden, da die Geraden und 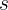parallel sind.
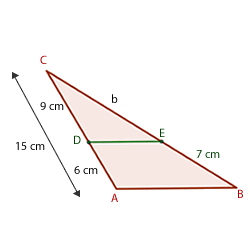
Wir wissen, dass das Segment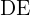 
parallel zur Grundseite des Dreiecks ist. Die Maße der Segmente und 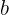sind...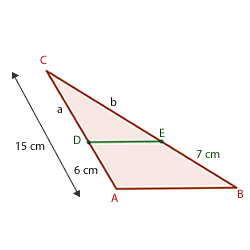 
Bitte wähle eine Antwort aus.
Zunächst ist 
, wir rechnen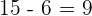 
. 
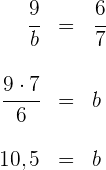
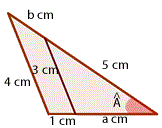
Die Segmente, die 3 cm und 4 cm lang sind, sind parallel. Berechne und .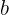 
Bitte wähle eine Antwort aus.
Die Dreiecke fallen unter den Satz des Thales, da sie den Winkel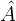 
gemeinsam haben und die Seiten mit den Längen 3 cm und 4 cm parallel sind. Wir wenden den Satz des Thales an:
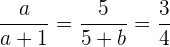
Wir erarbeiten die Gleichung, die aus dem ersten und dem letzten Teil besteht, und lösen nach auf
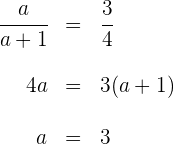
Die letzte Gleichung lösen wir nach 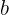auf
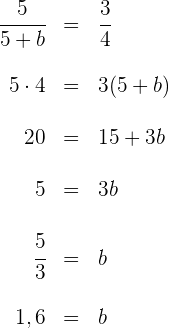
Wenn wir die Höhe der Bücher mit benennen und den Satz des Thales anwenden,
Dieses Feld ist erforderlich.
Wir benennen die Höhe der Bücher mit und wenden den Satz des Thales an
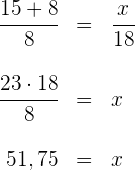
Berechne die Länge des Seils, das die Sprossen der Leiter mit der Rückseite der Leiter verbindet, wenn du die Leiter in der Zeichnung betrachtest.
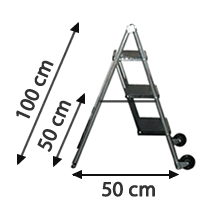
cm
Dieses Feld ist erforderlich.
Wir benennen die Länge der Sehne mit 
und wenden den Satz des Thales an
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
