Was ist ein Vieleck?
Ein Vieleck ist eine ebene Figur, die durch eine endliche Anzahl von geraden Liniensegmenten beschrieben wird, die miteinander verbunden sind, um eine geschlossene polygonale Kette oder einen polygonalen Kreis zu bilden. Der Bereich der Volumenebene, der Begrenzungskreis oder beides zusammen kann als Vieleck bezeichnet werden.
Merkmale eines Vielecks
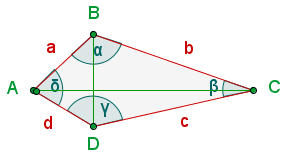
Seiten
Die Seiten eines Vielecks sind die Segmente, die es begrenzen.
Scheitelpunkte
Scheitelpunkte sind die Punkte, an denen sich zwei Seiten treffen. In der obigen Abbildung sind die Scheitelpunkte die Punkte 
, 
, 
und 
.
Innenwinkel
Die Innenwinkel werden durch zwei aufeinanderfolgende Seiten bestimmt.
In der obigen Abbildung hast du die Winkel 
, 
, , und 
.
Um die Innenwinkel eines Vielecks zu addieren - 
steht für die Anzahl der Seiten - gibt es die folgende Formel:
Summe der Innenwinkel eines Vielecks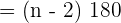 
Diagonale
Die Diagonalen sind die Segmente, die zwei nicht aufeinanderfolgende Scheitelpunkte verbinden. In der vorhergehenden Abbildung hast du zwei Diagonalen, das Segment, das die Scheitelpunkte und verbindet, und das Segment, das die Scheitelpunkte und verbindet.
Um die Anzahl der Diagonalen eines Vielecks zu ermitteln - steht für die Anzahl der Seiten - kannst du die folgende Formel verwenden:
Anzahl der Diagonalen eines Vielecks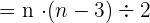 
Beispiele für die Berechnung von Diagonalen
1 Berechne die Anzahl der Diagonalen des folgenden 
-seitigen Vielecks.
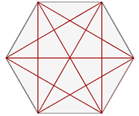
2 Berechne die Anzahl der Diagonalen des folgenden 
-seitigen Vielecks.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
