Kapitel
- Zusammenfassung zu Flächen und Umfängen geometrischer Figuren in der Ebene
- Fläche, Umfang und Diagonale eines Quadrats
- Fläche, Umfang und Diagonale eines Rechtecks
- Fläche und Umfang einer Raute
- Fläche und Umfang eines Parallelogramms
- Fläche und Umfang eines Trapezes
- Fläche und Umfang eines Dreiecks
- Fläche eines Vielecks
- Fläche und Umfang eines regelmäßigen Vielecks

Zusammenfassung zu Flächen und Umfängen geometrischer Figuren in der Ebene
Umfang eines Vielecks:
Sie ist die Summe der Seitenlängen eines Vielecks.
Fläche eines Vielecks:
Sie ist das Maß für den Bereich oder die Fläche, die von einer ebenen Figur umschlossen wird.
Fläche, Umfang und Diagonale eines Quadrats

Fläche eines Quadrats: Ist gleich dem Quadrat der Länge einer seiner Seiten.

Umfang eines Quadrats: Ist gleich der Summe seiner Seiten; da diese gleich sind, ist der Umfang gleich.

Diagonale eines Quadrats: Ist gleich der Seite multipliziert mit 

Beispiel
Berechne die Fläche, den Umfang und die Diagonale eines Quadrats mit einer Seitenlänge von  .
.

Die Seite 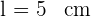 . Wir berechnen den Umfang
. Wir berechnen den Umfang
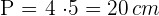
Wir berechnen die Fläche
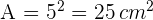
Wir berechnen die Diagonale

Fläche, Umfang und Diagonale eines Rechtecks
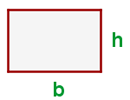
Fläche eines Rechtecks: Entspricht dem Produkt aus Grundseite und Höhe
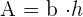
Umfang eines Rechtecks: Entspricht der Summe der Seiten; da die parallelen Seiten gleich sind, gilt

Diagonale eines Rechtecks: Entspricht der Quadratwurtel der Summe des Quadrats aus Grundseite und Höhe zum Quadrat

Beispiel
Berechne die Fläche, den Umfang und die Diagonale eines Rechtecks mit einer Grundseite von 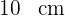 und einer Höhe von
und einer Höhe von  .
.
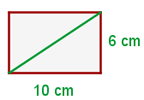
Wir berechnen den Umfang
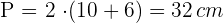
Wir berechnen die Fläche

Wir berechnen die Diagonale
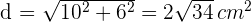
Fläche und Umfang einer Raute
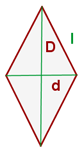
Fläche einer Raute: Entspricht der Hälfte des Produkts der Diagonalen

Umfang einer Raute: Entspricht der Summe der vier Seiten; da diese gleich sind, gilt

Beispiel
Berechne die Fläche einer Raute, deren Diagonalen  und
und 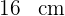 sind. Eine Seite misst
sind. Eine Seite misst  .
.
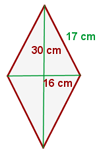
Wir berechnen den Umfang

Wir berechnen die Fläche

Fläche und Umfang eines Parallelogramms
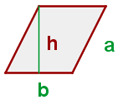
Fläche eines Parallelogramms: Entspricht dem Produkt aus Grundseite und Höhe
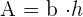
Unfang eines Parallelogramms: Entspricht der doppelten Summe zweier aufeinanderfolgender Seiten
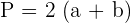
Beispiel
Berechne die Fläche eines Parallelogramms mit einer Seitenlänge von  und
und 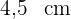 und einer Höhe von
und einer Höhe von  .
.
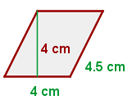
Wir berechnen den Umfang
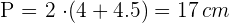
Wir berechnen die Fläche
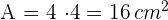
Fläche und Umfang eines Trapezes
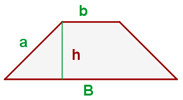
Fläche eines Trapezes: Entspricht der Hälfte des Produkts aus der Summe der Grundseiten und der Höhe

Umfang eines Trapezes: Entspricht der Summe der vier Seiten
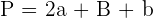
Beispiel
Ermittle den Flächeninhalt des folgenden Trapezes
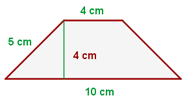
Wir berechnen den Umfang

Wir berechnen die Fläche
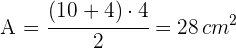
Fläche und Umfang eines Dreiecks
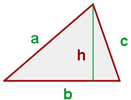
Fläche eines Dreiecks: Entspricht der Hälfte des Produkts aus seiner Grundfläche und seiner Höhe

Umfang eines Dreiecks: Entspricht der Summe der drei Seiten

Beispiel
Berechne die Fläche des folgenden Dreiecks
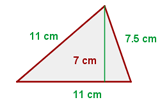
Es handelt sich um ein gleichschenkliges Dreieck, daher ist der Umfang
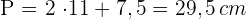
Die Grundseite misst  und die Höhe
und die Höhe 
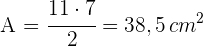
Fläche eines Vielecks
Fläche eines Vielecks: Erhält man durch die Einteilung des Vielecks in Dreiecke und die Addition der Flächen dieser Dreiecke.

Fläche und Umfang eines regelmäßigen Vielecks
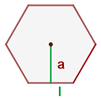
Fläche eines regelmäßigen Vielecks: Ist gleich der Hälfte seines Umfangs mal seinem Apothema

Umfang eines regelmäßigen Vielecks: Entspricht der Summe aller Seiten; da die Seiten gleich sind, gilt für 
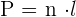
Beispiel
Berechne die Fläche eines regelmäßigen Fünfecks mit einer Seitenlänge von  und mit einem Abstand der Eckpunkte vom Mittelpunkt von
und mit einem Abstand der Eckpunkte vom Mittelpunkt von  .
.
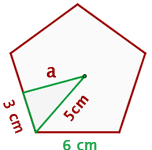
Wir berechnen den Umfang
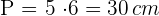
Wir berechnen den Flächeninhalt. Dazu wenden wir den Satz des Pythagoras an und erhalten den Wert des Apothemas
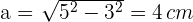
Wir setzen den Umfang und das Apothema in die Formel für den Flächeninhalt ein
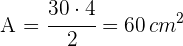
Mit KI zusammenfassen:












