Ein rechteckiges Feld hat eine Grundseite von  m und eine Höhe von
m und eine Höhe von  m. Berechne:
m. Berechne:
A Seine Größe in Hektar.
B Den Preis des Feldes, wenn der Quadratmeter  € kostet.
€ kostet.
A Wir berechnen die Fläche des Rechtecks, indem wir die Grundseite mit der Höhe multiplizieren
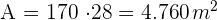
Wir wissen, dass ein Hektar 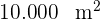 entspricht, sodass die Anzahl der Hektar des Rechtecks wie folgt ist
entspricht, sodass die Anzahl der Hektar des Rechtecks wie folgt ist
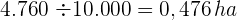
B Um den Preis des Feldes zu berechnen, wenn der Quadratmeter  € kostet, berechnen wir wie folgt
€ kostet, berechnen wir wie folgt
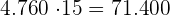 €
€
Berechne die Anzahl der quadratischen Fliesen mit einer Seitenlänge von  cm, die benötigt werden, um eine rechteckige Fläche von
cm, die benötigt werden, um eine rechteckige Fläche von  m Grundseite und
m Grundseite und  m Höhe zu fliesen.
m Höhe zu fliesen.
1 Wir berechnen die Fläche des Rechtecks, indem wir die Grundseite mit der Höhe multiplizieren
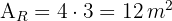
2 Wir wissen, dass 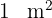 gleich
gleich 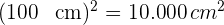 ist, also ist die Fläche des Rechtecks in Quadratzentimetern
ist, also ist die Fläche des Rechtecks in Quadratzentimetern
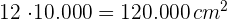
3 Wir berechnen die Fläche einer Fliese
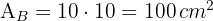
4 Um die Anzahl der benötigten Fliesen zu berechnen, wird die Fläche des Rechtecks durch die Fläche einer Fliese geteilt
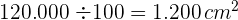
Es werden also 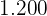 Fliesen benötigt.
Fliesen benötigt.
Ermittle den Flächeninhalt eines gleichschenkligen und rechtwinkligen Dreiecks, dessen Seiten jeweils  cm messen.
cm messen.
1 Wir zeichnen das gleichschenklige, rechtwinklige Dreieck
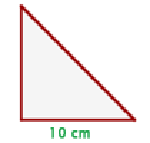
2 Wir stellen fest, dass die gleichen Seiten der Grundseite und der Höhe des Dreiecks 3 Wir berechnen den Flächeninhalt des Dreiecks, der gleich dem Produkt aus der Grundseite und der Höhe geteilt durch 2 ist
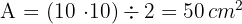
Der Umfang eines gleichseitigen Dreiecks beträgt  dm und die Höhe beträgt
dm und die Höhe beträgt 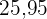 cm. Berechne den Flächeninhalt des Dreiecks.
cm. Berechne den Flächeninhalt des Dreiecks.
1 Wir zeichnen das gleichseitige Dreieck
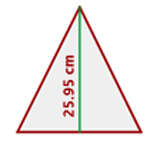
2 Wir stellen fest, dass der Umfang in  und die Höhe in
und die Höhe in  angegeben ist. Wir rechnen den Umfang in Zentimeter um
angegeben ist. Wir rechnen den Umfang in Zentimeter um
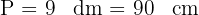
3 Um die Fläche des Dreiecks zu berechnen, müssen wir seine Grundseite und seine Höhe kennen. Da das Dreieck gleichseitig ist, sind seine drei Seiten gleich lang, so dass man eine Seite erhält, indem man den Umfang durch drei teilt
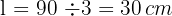
4 Wir berechnen den Flächeninhalt des Dreiecks, der gleich dem Produkt aus der Grundseite mal der Höhe geteilt durch 2 ist
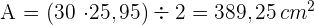
Berechne die Anzahl der Bäume, die auf einer rechteckigen Fläche von  Länge und
Länge und  Breite gepflanzt werden können, wenn jede Pflanze
Breite gepflanzt werden können, wenn jede Pflanze 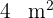 zum Wachsen benötigt.
zum Wachsen benötigt.
1 Wir berechnen den Flächeninhalt der rechteckigen Fläche, der gleich dem Produkt aus Länge und Breite ist
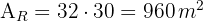
2 Da jeder Baum 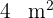 benötigt, dividieren wir die Fläche durch 4
benötigt, dividieren wir die Fläche durch 4
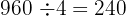
Somit können  Bäume gepflanzt werden
Bäume gepflanzt werden
Der Flächeninhalt eines Trapezes ist 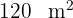 , die Höhe
, die Höhe  und die kleinere Grundseite misst
und die kleinere Grundseite misst  . Wie lang ist die andere Grundseite?
. Wie lang ist die andere Grundseite?
1 Wir schreiben die Formel für die Fläche eines Trapezes, die gleich der Hälfte des Produkts aus Höhe und Summe der Grundseiten ist

2 Wir setzen die uns bekannten Werte ein
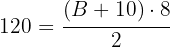
3 Wir vereinfachen die rechte Seite, indem wir durch 2 teilen

4 Nun möchten wir  bestimmen. Wir teilen also beide Seiten durch 4 und erhalten
bestimmen. Wir teilen also beide Seiten durch 4 und erhalten

5 Wir substrahieren 10 auf beiden Seiten und erhalten
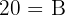
Die andere Grundseite misst also 
Berechne den Flächeninhalt eines Parallelogramms, dessen Höhe  cm und dessen Grundseite das
cm und dessen Grundseite das  -Fache seiner Höhe beträgt.
-Fache seiner Höhe beträgt.
1 Um die Fläche zu berechnen, müssen wir die Grundseite und die Höhe kennen. Die Höhe beträgt 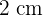 und die Grundseite ist das 3-Fache ihrer Höhe, also ist der Wert der Grundseite
und die Grundseite ist das 3-Fache ihrer Höhe, also ist der Wert der Grundseite
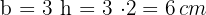
2 Wir berechnen die Fläche, die gleich dem Produkt aus Grundseite und Höhe ist.
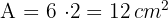
Berechne den Flächeninhalt eines Rhombus, dessen längste Diagonale  cm misst und dessen kürzeste Diagonale die Hälfte der längsten Diagonale ist.
cm misst und dessen kürzeste Diagonale die Hälfte der längsten Diagonale ist.
1 Um die Fläche zu berechnen, müssen wir die Hauptdiagonale und die Nebendiagonale des Rhombus kennen. Die Hauptdiagonale misst  und die Nebendiagonale misst die Hälfte der Hauptdiagonale, also ist der Wert der Nebendiagonale
und die Nebendiagonale misst die Hälfte der Hauptdiagonale, also ist der Wert der Nebendiagonale

2 Wir berechnen die Fläche, die gleich dem halben Produkt der Diagonalen ist

In der Mitte eines quadratischen Gartens von  m Seitenlänge befindet sich ein quadratischer Pool von ebenfalls
m Seitenlänge befindet sich ein quadratischer Pool von ebenfalls  m Länge.
m Länge.
1 Wir stellen die Aufgabe grafisch dar und stellen fest, dass die Gesamtfläche gleich der Fläche des Gartens plus der Fläche des Pools ist

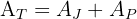
2 Wir berechnen die Gesamtfläche, die gleich dem Produkt der Seiten des Quadrats ist
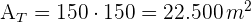
3 Wir berechnen die Fläche des Pools, die gleich dem Produkt der Seiten des Quadrats ist
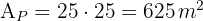
4 Die Fläche des Gartens ist also gleich der Gesamtfläche abzüglich der Fläche des Pools.
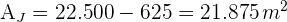
Berechne den Flächeninhalt des Vierecks, das sich aus der Verbindung der Mittelpunkte der Seiten eines Rechtecks ergibt, dessen Grundseite und Höhe  und
und  cm betragen.
cm betragen.
1 Wir stellen die Aufgabe grafisch dar und stellen fest, dass die Gesamtfläche gleich vier rechtwinkligen Dreiecken mit der Grundseite  und der Höhe
und der Höhe 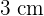 ist
ist

2 Wir berechnen die Fläche des Dreiecks
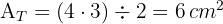
3 Wir berechnen den Flächeninhalt des Vierecks

Wie groß ist die Fläche des hervorgehobenen Teils der Abbildung, wenn die Fläche des Sechsecks 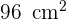 beträgt.
beträgt.
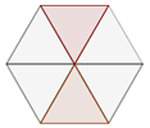
1 Wir sehen, dass das Sechseck aus 6 gleichen Dreiecken zusammengesetzt ist
2 Wir berechnen den Flächeninhalt eines Dreiecks

3 Wir berechnen die hervorgehobene Fläche
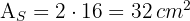
Eine bewaldete Fläche hat die Form eines Trapezes, dessen Grundseiten  m und
m und  m messen. Die Breite der Fläche beträgt
m messen. Die Breite der Fläche beträgt  m. Ein
m. Ein  m breiter Weg wird rechtwinklig zu den beiden Grundflächen angelegt. Berechne die Fläche der verbleibenden bewaldeten Fläche.
m breiter Weg wird rechtwinklig zu den beiden Grundflächen angelegt. Berechne die Fläche der verbleibenden bewaldeten Fläche.
1 Wir stellen die Aufgabe grafisch dar und stellen fest, dass die Fläche des Trapezes gleich der Summe aus der Fläche des Waldes und der Fläche des Weges ist

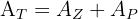
2 Wir berechnen den Flächeninhalt des Trapezes
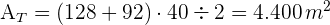
3 Wir berechnen die Fläche des Weges

4 Wir berechnen die Fläche des bewaldeten Bereichs
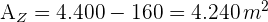
Ein rechteckiger Garten hat die Maße  m und
m und  m. Der Garten wird von zwei senkrecht zueinander verlaufenden Wegen durchquert, die ein Kreuz bilden. Der eine hat eine Breite von
m. Der Garten wird von zwei senkrecht zueinander verlaufenden Wegen durchquert, die ein Kreuz bilden. Der eine hat eine Breite von  dm und der andere von
dm und der andere von  dm. Berechne die Fläche des Gartens.
dm. Berechne die Fläche des Gartens.
1 Wir stellen die Aufgabe grafisch dar und stellen fest, dass die Fläche des Gartens gleich der Fläche des Rechtecks minus der Fläche der Wege plus der Fläche der Überschneidung der Wege ist
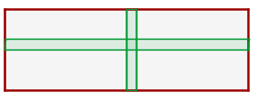

2 Wir berechnen den Flächeninhalt des Rechtecks

3 Wir berechnen die Fläche des ersten Weges
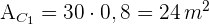
4 Wir berechnen die Fläche des zweiten Weges
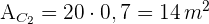
5 Wir berechnen die Fläche der Überschneidung der Wege
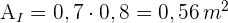
6 Wir berechnen die Fläche des Gartens
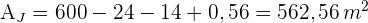
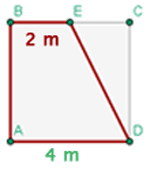
Das Quadrat  mit der Seitenlänge
mit der Seitenlänge  m verbindet
m verbindet  , den Mittelpunkt der Strecke
, den Mittelpunkt der Strecke  , mit dem Scheitelpunkt
, mit dem Scheitelpunkt  . Berechne den Flächeninhalt des gebildeten Trapezes.
. Berechne den Flächeninhalt des gebildeten Trapezes.
1 Wir stellen die Aufgabe grafisch dar und stellen fest, dass die Fläche des Trapezes gleich der Fläche des Quadrats minus der Fläche des rechtwinkligen Dreiecks ist

2 Wir berechnen die Fläche des Quadrats

3 Wir berechnen den Flächeninhalt des Dreiecks
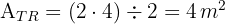
4 Wir berechnen den Flächeninhalt des Trapezes
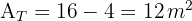
Berechne die Menge an Farbe, die für den Anstrich der Fassade dieses Gebäudes benötigt wird, wobei  kg Farbe pro
kg Farbe pro  verwendet werden.
verwendet werden.
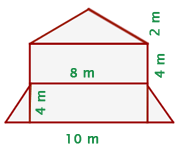
1 Wir stellen fest, dass die Fläche des Gebäudes durch ein Dreieck mit der Grundseite  und der Höhe
und der Höhe 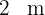 , zwei Rechtecke mit der Grundseite
, zwei Rechtecke mit der Grundseite  und der Höhe
und der Höhe 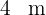 und zwei Rechtecke mit der Grundseite
und zwei Rechtecke mit der Grundseite 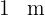 und der Höhe
und der Höhe 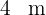 gebildet wird:
gebildet wird:

2 Wir berechnen den Flächeninhalt des Dreiecks
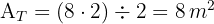
3 Wir berechnen den Flächeninhalt des Rechtecks

4 Wir berechnen den Flächeninhalt des rechtwinkligen Dreiecks

5 Wir berechnen die Fläche des Gebäudes

6 Wir berechnen die für den Anstrich des Gebäudes benötigten Kilogramm Farbe
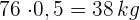
Ermittle den Umfang und die Fläche der Figur:

1 Wir stellen fest, dass die Figur ein Parallelogramm mit der Grundseite  und der Höhe
und der Höhe 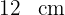 bildet; ein rechtwinkliges Dreieck mit der Grundseite
bildet; ein rechtwinkliges Dreieck mit der Grundseite  und der Höhe
und der Höhe 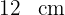 , sodass sein Flächeninhalt beträgt
, sodass sein Flächeninhalt beträgt

2 Wir berechnen den Flächeninhalt des Dreiecks

3 Wir berechnen die Fläche des Parallelogramms
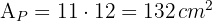
4 Wir berechnen den Flächeninhalt der Figur
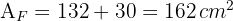
5 Wir berechnen den Umfang
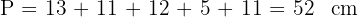
Mit KI zusammenfassen:



