
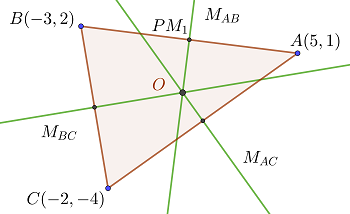
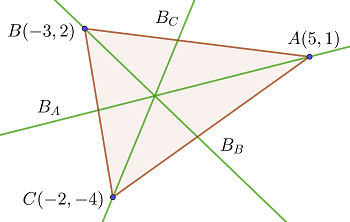
Grundlegende Elemente eines Dreiecks
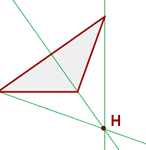
Höhen eines Dreiecks
Die Höhe ist jede der senkrechten Linien, die von einem Eckpunkt zur gegenüberliegenden Seite (oder ihrer Verlängerung) gezogen wird.
Höhenschnittpunkt/Orthozentrum
Der Schnittpunkt der drei Höhen.
Seitenhalbierende eines Dreiecks
Die Seitenhalbierende ist jede der Linien, die den Mittelpunkt einer Seite mit dem gegenüberliegenden Eckpunkt verbindet.
Schwerpunkt
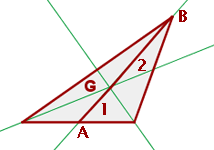
Der Schnittpunkt der drei Seitenhalbierenden.
Der Schwerpunkt, auch Baryzentrum genannt, teilt jede Seitenhalbierende in zwei Segmente, wobei das Segment, das den Schwerpunkt mit dem Eckpunkt verbindet, doppelt so lang ist wie das Segment, das den Schwerpunkt mit dem Mittelpunkt der gegenüberliegenden Seite verbindet.
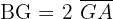
Mittelsenkrechten eines Dreiecks
Die Mittelsenkrechte ist jede der senkrechten Linien, die durch den Mittelpunkt einer Seite gezogen wird.
Umkreismittelpunkt
Der Schnittpunkt der drei Mittelsenkrechten.
Es ist der Mittelpunkt eines Kreises, der das Dreieck umschreibt.
Winkelhalbierende eines Dreiecks
Die Winkelhalbierende ist jede der Geraden, die einen Winkel in zwei gleiche Winkel teilt.
Inkreis
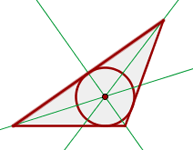
Der Schnittpunkt der drei Winkelhabierenden.
Es ist der Mittelpunkt eines in das Dreieck eingeschriebenen Kreises.
Eulersche Gerade
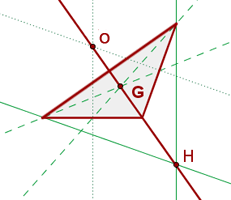
Der Höhenschnittpunkt, der Schwerpunkt und der Umkreismittelpunkt eines unregelmäßigen Dreiecks sind zueinander ausgerichtet, d.h. sie gehören zur selben Linie, die Eulersche Gerade genannt wird.
Aufgaben mit Lösungen
Gegeben ist ein Dreieck mit den Eckpunkten 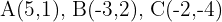 . Berechne:
. Berechne:
die Höhen
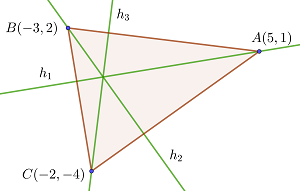
1 Gesucht ist die Gleichung der Höhe 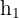 , die durch den Eckpunkt
, die durch den Eckpunkt  und die ihm gegenüberliegende Seite verläuft.
und die ihm gegenüberliegende Seite verläuft.
Da die Höhe senkrecht auf der gegenüberliegenden Seite steht, berechnen wir die Steigung  der Seite
der Seite  .
.
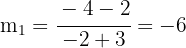
Die Steigung 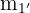 der Höhe ist
der Höhe ist
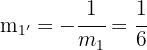
Die Höhe 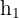 hat die Steigung
hat die Steigung 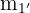 und verläuft durch den Punkt
und verläuft durch den Punkt  . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung
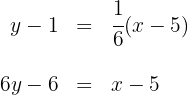
Somit lautet die Gleichung der Höhe 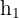 es
es 
2 Gesucht ist die Gleichung der Höhe 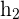 , die durch den Eckpunkt
, die durch den Eckpunkt  und die ihm gegenüberliegende Seite verläuft.
und die ihm gegenüberliegende Seite verläuft.
Da die Höhe senkrecht auf der gegenüberliegenden Seite steht, berechnen wir die Steigung  der Seite
der Seite 

Die Steigung 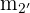 der Höhe ist
der Höhe ist
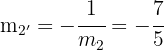
Die Höhe 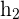 hat die Steigung
hat die Steigung 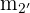 und verläuft durch den Punkt
und verläuft durch den Punkt  . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung
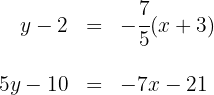
Die Gleichung der Höhe 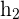 ist also
ist also 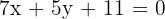
3 Gesucht ist die Gleichung der Höhe 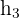 , die durch den Eckpunkt
, die durch den Eckpunkt  und die ihm gegenüberliegende Seite verläuft.
und die ihm gegenüberliegende Seite verläuft.
Da die Höhe senkrecht auf der gegenüberliegenden Seite steht, berechnen wir die Steigung 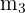 der Seite
der Seite 

Die Steigung 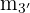 der Höhe lautet
der Höhe lautet
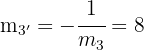
Die Höhe 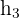 hat die Steigung
hat die Steigung 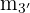 und verläuft durch den Punkt
und verläuft durch den Punkt  . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung
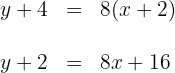
Somit lautet die Gleichung der Höhe 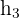 es
es 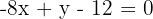
den Höhenschnittpunkt
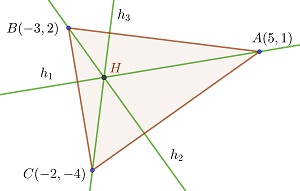
1 Gesucht ist der Schnittpunkt der Höhen  . Hierfür multiplizieren wir die 1. Höhe mit 7 und addieren die 2. Höhe, um die 2. Koordinate des Höhenschnittpunkts zu erhalten
. Hierfür multiplizieren wir die 1. Höhe mit 7 und addieren die 2. Höhe, um die 2. Koordinate des Höhenschnittpunkts zu erhalten

2 Wir setzen den Wert der 2. Koordinate des Höhenschnittpunkts in die Gleichung der 1. Höhe ein und lösen, um die 1. Koordinate des Höhenschnittpunktes zu berechnen
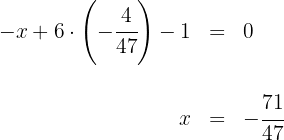
3 Wir überprüfen, ob der Höhenschnittpunkt zur Höhe 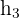 gehört
gehört

die Gleichheit ist erfüllt, weshalb der Höhenschnittpunkt 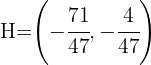 der Schnittpunkt der drei Höhen ist
der Schnittpunkt der drei Höhen ist
die Seitenhalbierenden
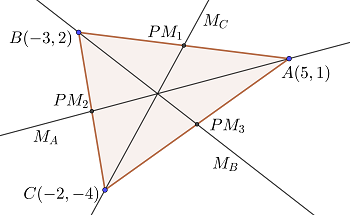
1 Gesucht sind die Mittelpunkte der Seiten des Dreiecks
Der Mittelpunkt 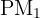 der Seite
der Seite  ist
ist
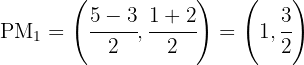
Der Mittelpunkt  der Seite
der Seite  ist
ist

Der Mittelpunkt 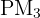 der Seite
der Seite  ist
ist

2 Gesucht ist die Gleichung der Seitenhalbierenden 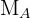 , die durch den Eckpunkt
, die durch den Eckpunkt  und den Mittelpunkt der gegenüberliegenden Seite verläuft
und den Mittelpunkt der gegenüberliegenden Seite verläuft
Wir berechnen die Steigung, die durch  und
und  verläuft
verläuft

Die Seitenhalbierende 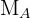 hat die Steigung
hat die Steigung  und verläuft durch den Punkt
und verläuft durch den Punkt  . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung
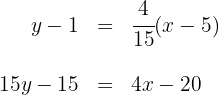
Die Gleichung der Seitenhalbierenden 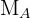 ist also
ist also 
3 Gesucht ist die Gleichung der Seitenhalbierenden  , die durch den Eckpunkt
, die durch den Eckpunkt  und den Mittelpunkt der gegenüberliegenden Seite verläuft
und den Mittelpunkt der gegenüberliegenden Seite verläuft
Wir berechnen die Steigung, die durch  und
und 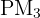 verläuft
verläuft
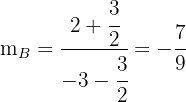
Die Seitenhalbierende  hat die Steigung
hat die Steigung 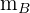 und verläuft durch den Punkt
und verläuft durch den Punkt  . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung
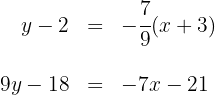
Die Gleichung der Seitenhalbierenden  ist also
ist also 
4 Gesucht ist die Gleichung der Seitenhalbierenden  , die durch den Eckpunkt
, die durch den Eckpunkt  und den Mittelpunkt der gegenüberliegenden Seite verläuft
und den Mittelpunkt der gegenüberliegenden Seite verläuft
Wir berechnen die Steigung, die durch  und
und  verläuft
verläuft

Die Seitenhalbierende  hat die Steigung
hat die Steigung  und verläuft durch den Punkt
und verläuft durch den Punkt  . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung
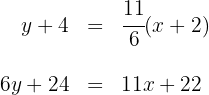
Die Gleichung der Seitenhalbierenden  ist also
ist also 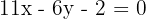
den Schwerpunkt
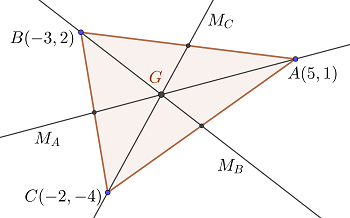
1 Gesucht ist der Schnittpunkt der Seitenhalbierenden  . Hierfür multiplizieren wir die 1. Seitenhalbierende mit
. Hierfür multiplizieren wir die 1. Seitenhalbierende mit  , die 2. Seitenhalbierende mit
, die 2. Seitenhalbierende mit  und addieren die beiden Seitenhalbierenden, um die 2. Koordinate des Schwerpunktes zu erhalten
und addieren die beiden Seitenhalbierenden, um die 2. Koordinate des Schwerpunktes zu erhalten

2 Wir setzen den Wert der 2. Koordinate des Schwerpunktes in die Gleichung der 2. Seitenhalbierenden ein und berechnen, um die 1. Koordinate des Schwerpunktes zu erhalten
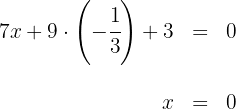
3 Wir überprüfen, ob der Schwerpunkt zur Seitenhalbierenden  gehört
gehört
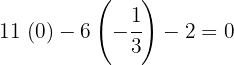
die Gleichheit ist erfüllt, weshalb der Schwerpunkt 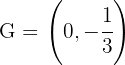 der Schnittpunkt der drei Seitenhalbierenden ist
der Schnittpunkt der drei Seitenhalbierenden ist
die Mittelsenkrechten
1 Gesucht sind die Mittelpunkt der Seiten des Dreiecks
Der Mittelpunkt 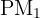 der Seite
der Seite  ist
ist
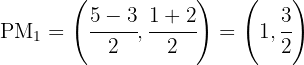
Der Mittelpunkt  der Seite
der Seite  ist
ist

Der Mittelpunkt 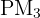 der Seite
der Seite  ist
ist

2 Gesucht ist die Gleichung der Mittelsenkrechten  , die durch den Mittelpunkt von
, die durch den Mittelpunkt von  verläuft und darauf senkrecht steht.
verläuft und darauf senkrecht steht.
Wir berechnen die Steigung  der Seite
der Seite 
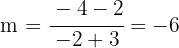
Die Steigung 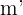 der Mittelsenkrechten ist
der Mittelsenkrechten ist

Die Mittelsenkrechte  hat die Steigung
hat die Steigung  und verläuft durch den Punkt
und verläuft durch den Punkt  . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung
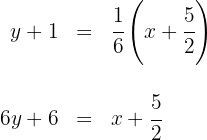
Die Gleichung der Mittelsenkrechten  ist
ist 
3 Gesucht ist die Gleichung der Mittelsenkrechten  , die durch den Mittelpunkt von
, die durch den Mittelpunkt von  verläuft und darauf senkrecht steht.
verläuft und darauf senkrecht steht.
Wir berechnen die Steigung  der Seite
der Seite 

Die Steigung 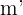 der Mittelsenkrechten ist
der Mittelsenkrechten ist
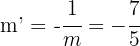
Die Mittelsenkrechte  hat die Steigung
hat die Steigung 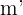 und verläuft durch den Punkt
und verläuft durch den Punkt 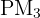 . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung
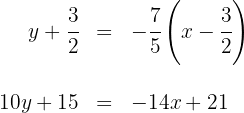
Die Gleichung der Mittelsenkrechten  ist
ist 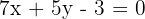
4 Gesucht ist die Gleichung der Mittelsenkrechten  , die durch den Mittelpunkt von
, die durch den Mittelpunkt von  verläuft und darauf senkrecht steht.
verläuft und darauf senkrecht steht.
Wir berechnen die Steigung  der Seite
der Seite 

Die Steigung 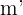 der Mittelsenkrechten ist
der Mittelsenkrechten ist

Die Mittelsenkrechte  hat die Steigung
hat die Steigung 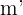 und verläuft durch den Punkt
und verläuft durch den Punkt 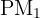 . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung

Die Gleichung der Höhe  ist
ist 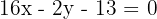
den Umkreis
1 Wir suchen den Schnittpunkt der Mittelsenkrechten 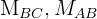 . Hierfür multiplizieren wir die 1. Mittelsenkrechte mit
. Hierfür multiplizieren wir die 1. Mittelsenkrechte mit  und addieren die beiden Mittelsenkrechten, um die 2. Koordinate des Umkreismittelpunktes zu erhalten
und addieren die beiden Mittelsenkrechten, um die 2. Koordinate des Umkreismittelpunktes zu erhalten
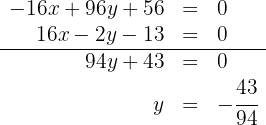
2 Wir setzen den Wert der 2. Koordinate des Umkreismittelpunktes in die Gleichung der 2. Mittelsenkrechten ein und berechnen, um die 1. Koordinate des Umkreismittelpunktes zu erhalten
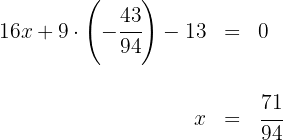
3 Wir überprüfen, ob der Umkreismittelpunkt zur Mittelsenkrechten  gehört
gehört
7x + 5y - 3
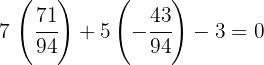
die Gleichheit ist erfüllt, weshalb der Umkreismittelpunkt  der Schnittpunkt der drei Mittelsenkrechten ist
der Schnittpunkt der drei Mittelsenkrechten ist
die Winkelhalbierenden
1 Um die Gleichung einer Winkelhalbierenden zu finden, genügt es, den Abstand der Punkte der Winkelhalbierenden mit den Seiten des betreffenden Winkels gleichzusetzen, d. h., wenn die Seiten, die die Winkel bilden, wie folgt sind:
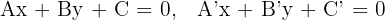
somit erhält man die Winkelhalbierende:

2 Gesucht ist die Gleichung der Winkelhalbierenden von  . Hierfür müssen wir die Gleichungen der Seiten
. Hierfür müssen wir die Gleichungen der Seiten  und
und  ermitteln. Mit der Gleichung der Geraden durch zwei Punkte erhalten wir:
ermitteln. Mit der Gleichung der Geraden durch zwei Punkte erhalten wir:
die Gerade 

die Gleichung lautet
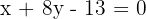
die Gerade 
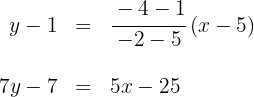
die Gleichung lautet

Wir wenden die Formel an, um die Winkelhalbierende zu ermitteln

Die Gleichung der Winkelhalbierenden 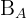 ist
ist
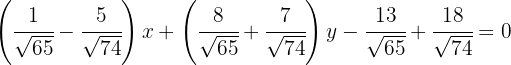
3 Gesucht ist die Gleichung der Winkelhalbierenden von  . Hierfür müssen wir die Gleichungen der Seiten
. Hierfür müssen wir die Gleichungen der Seiten  und
und  ermitteln. Mit der Gleichung der Geraden durch zwei Punkte erhalten wir:
ermitteln. Mit der Gleichung der Geraden durch zwei Punkte erhalten wir:
die Gerade 

die Gleichung lautet
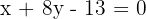
die Gerade 

die Gleichung lautet
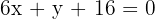
Wir wenden die Formel an, um die Winkelhalbierende zu ermitteln

Die Gleichung der Winkelhalbierenden 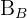 ist
ist

4 Gesucht ist die Gleichung der Winkelhalbierenden von  . Hierfür müssen wir die Gleichungen der Seiten
. Hierfür müssen wir die Gleichungen der Seiten  und
und  . Mit der Gleichung der Geraden durch zwei Punkte erhalten wir:
. Mit der Gleichung der Geraden durch zwei Punkte erhalten wir:
die Gerade 
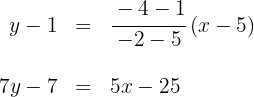
die Gleichung lautet

die Gerade 

die Gleichung lautet
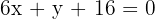
Wir wenden die Formel an, um die Winkelhalbierende zu ermitteln
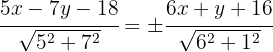
Die Gleichung der Winkelhalbierenden 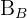 ist
ist
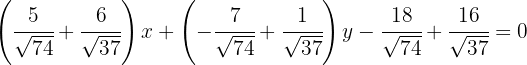
den Inkreismittelpunkt
1 Gesucht ist der Schnittpunkt der Winkelhalbierenden 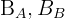 . Hierfür multiplizieren wir die 1. Winkelhalbierende mit
. Hierfür multiplizieren wir die 1. Winkelhalbierende mit 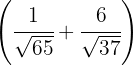 , mit
, mit 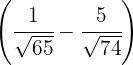 und addieren die beiden Winkelhalbierenden, um die 2. Koordinate des Inkreismittelpunktes zu erhalten
und addieren die beiden Winkelhalbierenden, um die 2. Koordinate des Inkreismittelpunktes zu erhalten

2 Wir setzen den Wert der 2. Koordinate des Inkreismittelpunktes in die 1. Gleichung der Winkelhalbierenden ein und berechnen, um die 1. Koordinate des Inkreismittelpunktes zu erhalten
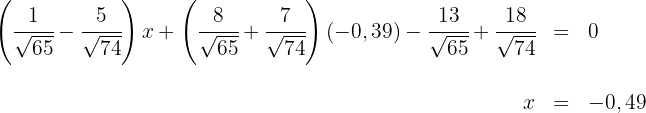
die Eulersche Gerade
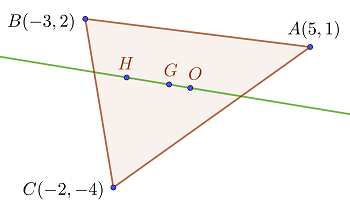
1 Gesucht ist die Gerade, die durch den Höhenschnittpunkt 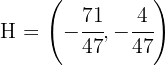 , den Schwerpunkt
, den Schwerpunkt 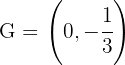 und den Umkreismittelpunkt
und den Umkreismittelpunkt  verläuft
verläuft
2Wir berechnen die Steigung  für den Höhenschnittpunkt und den Schwerpunkt
für den Höhenschnittpunkt und den Schwerpunkt
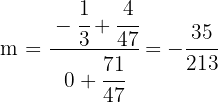
Die Eulersche Gerade hat die Steigung  und verläuft durch den Punkt
und verläuft durch den Punkt 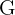 . Wir berechnen ihre Gleichung
. Wir berechnen ihre Gleichung

Somit lautet die Eulersche Gerade 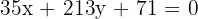
Zeige, dass der Inkreismittelpunkt nicht auf der Eulerschen Geraden liegt
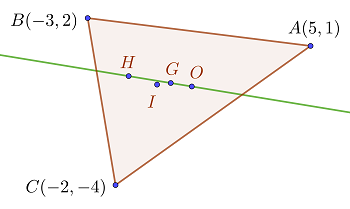
1 Es genügt, den Inkreismittelpunkt sustituir el incentro 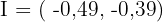 in die Eulersche Gerade einzusetzen und zu zeigen, dass diese nicht erfüllt ist
in die Eulersche Gerade einzusetzen und zu zeigen, dass diese nicht erfüllt ist
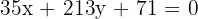
Wir setzen ein
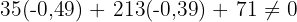
Da der Inkreismittelpunkt die Gleichung der Eulerschen Geraden nicht erfüllt, kann man daraus schließen, dass der Inkreismittelpunkt nicht auf der Eulerschen Geraden liegt.
Mit KI zusammenfassen:












