Kapitel
Ein Vieleck ist ein Bereich in der Ebene, der durch drei oder mehr Segmente begrenzt wird.

Elemente eines Vielecks
1 Seiten: Segmente, die es beschränken.
2 Eckpunkte: Punkte, an denen die Seiten zusammentreffen.
3 Innenwinkel eines Vielecks: Winkel, die durch zwei aufeinanderfolgende Seiten bestimmt werden.
4 Diagonale: Segmente, die zwei nicht aufeinanderfolgende Eckpunkte bestimmen.
Anzahl der Diagonalen eines Vielecks
Wenn  die Anzahl der Seiten eines Vielecks ist:
die Anzahl der Seiten eines Vielecks ist:
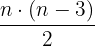
Regelmäßige Vieleck
Ein regelmäßiges Vieleck ist ein Vieleck mit gleichen Winkeln und gleichen Seiten.
Elemente eines regelmäßigen Vielecks
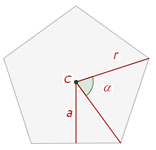
1 Mittelpunkt: Punkt im Inneren, der gleich weit von jedem Eckpunkt entfernt ist.
2 Radius: Das Segment vom Mittelpunkt zu jedem Eckpunkt.
3 Apothema: Strecke zwischen Mittelpunkt und Mittelpunkt einer Seite.
4 Winkel: gebildet durch zwei aufeinanderfolgende Radien
Beispiel:
Wenn  die Anzahl der Seiten eines Vielecks ist:
die Anzahl der Seiten eines Vielecks ist:
Mittelpunktswinkel 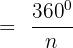
Innenwinkel 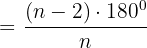
Eingeschriebenes Vieleck
Ein Vieleck ist in einen Kreis eingeschrieben, wenn alle seine Eckpunkte in ihm enthalten sind.
1 Umkreis
Berührt jeden Eckpunk des Vielecks.
Sein Mittelpunkt ist von allen Eckpunkten gleich weit entfernt.
Sein Radius ist der Radius des Vielecks.
2 Inkreis
Berührt das Vieleck am Mittelpunkt jeder Seite.
Sein Mittelpunkt ist von allen Seiten gleich weit entfernt.
Sei Radius ist das Apothema des Vielecks.
Dreiecke
Ein Dreieck ist ein Vieleck mit drei Seiten.
Eigenschaften von Dreiecken
1 Eine Seite eines Dreiecks ist kleiner als die Summe der beiden anderen und größer als deren Differenz.
2 Die Summe der Innenwinkel eines Dreiecks beträgt 180°.
3 Der Wert eines Außenwinkels ist gleich der Summe der beiden nicht benachbarten Innenwinkel.
Klassifizierung von Dreiecken nach ihren Seiten
1 Gleichseitiges Dreieck - Drei gleiche Seiten.

2 Gleichschenkliges Dreieck - Zwei gleiche Seiten.

3 Unregelmäßiges Dreieck - Drei ungleiche Seiten.
Klassifizierung von Dreiecken nach ihren Winkeln
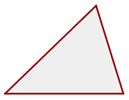
1 Spitzwinkliges Dreieck - Drei spitze Winkel
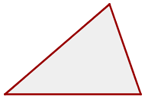
2 Rechtwinkliges Dreieck - Ein rechter Winkel. Die längste Seite ist die Hypotenuse. Die kürzeren Seiten sind die Katheten.
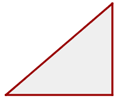
3 Stumpfwinkliges Dreieck - Ein stumpfer Winkel.
Elemente eines Dreiecks
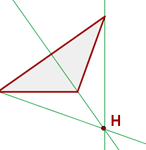
1 Die Höhe ist jede der senkrechten Geraden, die von einem Eckpunkt zur gegenüberliegenden Seite (oder ihrer Verlängerung) gezogen wird.
2 Das Orthozentrum ist der Schnittpunkt der drei Höhen.
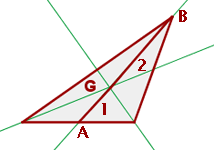
3 Die Seitenhalbierende ist jede der Geraden, die den Mittelpunkt einer Seite mit dem gegenüberliegenden Eckpunkt verbindet.
4 Der Schwerpunkt ist der Schnittpunkt der drei Seitenhalbierenden. Er teilt jede Seitenhalbierende in zwei Segmente.
Das Segment, das den Schwerpunkt mit dem Eckpunkt verbindet, ist doppelt so lang wie das Segment, das den Schwerpunkt mit dem Mittelpunkt der gegenüberliegenden Seite verbindet.
5 Die Mittelsenkrechte ist jede der senkrechten Geraden, die zu einer Seite durch ihren Mittelpunkt gezogen wird.
6 Der Umkreismittelpunkt ist der Schnittpunkt der drei Mittelsenkrechten. Er ist der Mittelpunkt eines Kreises, der das Dreieck umschreibt.
7 Die Winkelhalbierende ist jede der Geraden, die einen Winkel in zwei gleiche Winkel teilt.
8 Der Inkreismittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden. Er ist der Mittelpunkt eines in das Dreieck eingeschriebenen Kreises.
Eulersche Gerade
Das Orthozentrum, der Schwerpunkt und der Kreismittelpunkt eines nicht gleichseitigen Dreiecks liegen auf einer Geraden, der sogenannten Eulerschen Geraden.
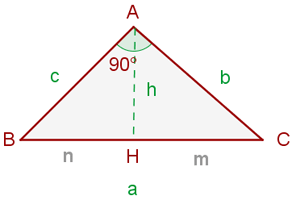
Kathetensatz
In jedem rechtwinkligen Dreieck ist eine Kathete ein halbes Größenverhältnis zwischen der Hypotenuse und ihrer Projektion auf die Hypotenuse.
Höhensatz
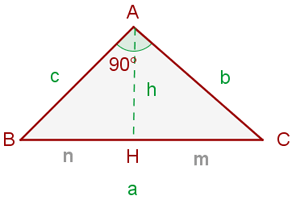
In einem rechtwinkligen Dreieck ist die Höhe in Bezug auf die Hypotenuse halb so groß wie die Höhe zwischen den beiden Segmenten, die die Hypotenuse teilen.
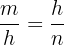
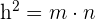
Satz des Pythagoras
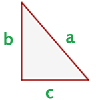
In einem rechtwinkligen Dreieck ist die Hypotenuse zum Quadrat gleich der Summe der Katheten zum Quadrat.

Um den Wert der Katheten oder der Hypotenuse zu ermitteln, werden die folgenden Formeln verwendet:
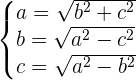
Der Kreis
Ein Kreis ist eine ebene Figur im Inneren eines Kreises.
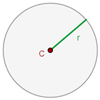
Elemente eines Kreises
Kreissegment - Der Teil eines Kreises, der durch eine Sehne und den entsprechenden Bogen begrenzt wird.

Halbkreis - Der Teil des Kreises, der durch einen Durchmesser und den entsprechenden Bogen begrenzt wird. Entspricht der Hälfte des Kreises.
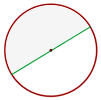
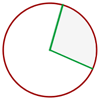
Kreiszone - Teil eines Kreises, der durch zwei Sehnen begrenzt wird.

Kreissektor - Teil eines Kreises, der durch zwei Radien begrenzt wird.
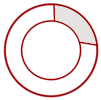
Kreisring - Der Teil eines Kreises, der von zwei konzentrischen Kreisen begrenzt wird.

Kreisring-Trapez - Teil eines Kreises, der von zwei Radien und einem Kreisring begrenzt wird.
Formeln für Flächen und Segmente des Kreises
Fläche eines Kreises
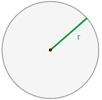
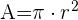
Beispiel:
Der Umfang eines Kreises beträgt 43,96 cm. Wie groß ist der Flächeninhalt des Kreises?
Wir haben 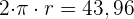 und bestimmen
und bestimmen 
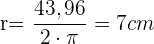
Nun setzen wir in die Formel für den Flächeninhalt des Kreises ein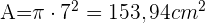
Fläche eines Kreissektors
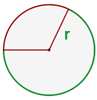
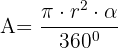
Beispiel
Finde die Fläche des Kreissektors, dessen Sehne die Seite des eingeschriebenen Quadrats ist, wobei 4 cm der Radius des Umfangs ist.
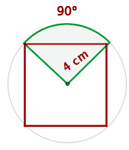
Wir haben  und
und  und wenden somit die Formel
und wenden somit die Formel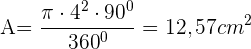 an
an
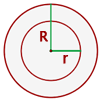
Fläche eines Kreisrings
Sie ist gleich der Fläche des größeren Kreises minus der Fläche des kleineren Kreises.
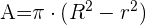
Beispiel:
In einem kreisförmigen Park mit einem Radius von 700 m befindet sich in der Mitte ein ebenfalls kreisförmiger Springbrunnen mit einem Radius von 5 m. Berechne die Fläche des begehbaren Bereichs.

Wir haben  und
und 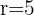 . Wir wenden die folgende Formel an
. Wir wenden die folgende Formel an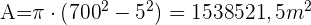
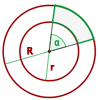
Fläche eines Kreisring-Trapezes
Sie ist gleich der Fläche des größeren Kreissektors minus der Fläche des kleineren Kreissektors.
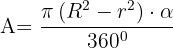
Beispiel:
Gegeben sind zwei konzentrische Kreise mit Radius 8 und 5 cm. Es werden die Radien OA und OB eingezeichnet, die einen Winkel von 60° bilden. Berechne die Fläche des Kreisring-Trapezes, das dadurch entsteht.
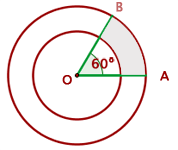
Wir haben 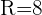 ,
, 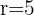 und
und 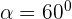 . Nun wenden wir folgende Formel an:
. Nun wenden wir folgende Formel an: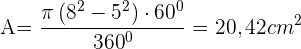 an
an
Fläche eines Kreissegments
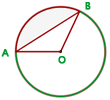
Fläche des Kreissegments AB = Fläche des Kreissektors AOB − Fläche des Dreiecks AOB
Beispiel:
In einen Kreis von 4 cm wird ein Mittelpunktswinkel von 60°eingezeichnet. Berechne die Fläche des Kreissegments zwischen der Sehne, die die Enden der beiden Radien verbindet, und dem entsprechenden Bogen.
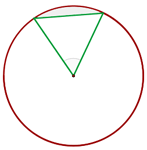
Zunächst berechnen wir die Fläche des Kreissektors mit der Formel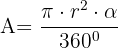 ,
,
wobei  und
und 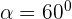 . Wir setzen ein:
. Wir setzen ein: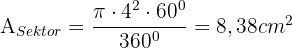
Jetzt berechnen wir die Fläche des gleichseitigen Dreiecks, also berechnen wir zuerst die Höhe. Wenn wir eine Höhe einzeichnen, erhalten wir zwei rechtwinklige Dreiecke und können den Satz des Pythagoras anwenden: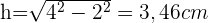
Der Flächeninhalt des Dreiecks ist dann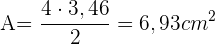
Die Fläche des Kreissegments ist schließlich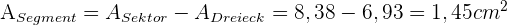
Der Kreisumfang
Der Kreisumfang ist eine geschlossene gekrümmte Linie, deren Punkte alle den gleichen Abstand zu einem festen Punkt, dem Mittelpunkt, haben.
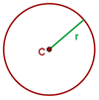
Der Mittelpunkt des Kreisumfangs ist der Punkt, von dem alle Punkte des Kreises gleich weit entfernt sind.
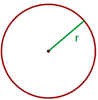
Der Radius des Kreisumfangs ist die Strecke, die den Kreismittelpunkt mit einem beliebigen Punkt des Kreises verbindet.
Elemente des Kreisumfangs
Sehne - Ein Segment, das zwei Punkte auf dem Kreisumfang verbindet.

Durchmesser - Sehne, die durch den Mittelpunkt verläuft.
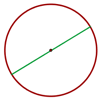
Bogen - Jeder der Teile, in die eine Sehne den Umfang unterteilt. Jede Sehne ist in der Regel mit dem kleinsten Bogen verbunden, den sie abgrenzt.
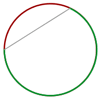
Halbkreisumfang - Der halbe Umfang des Kreises.
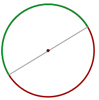
Winkel des Kreisumfangs
1 Mittelpunktswinkel
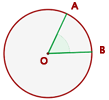
Der Mittelpunktswinkel hat seinen Scheitelpunkt in der Mitte des Kreises und seine Seiten sind zwei Radien.
Das Maß eines Bogens ist das Maß des entsprechenden Mittelpunktswinkels.

2 Umfangswinkel
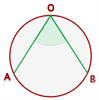
Der Umfangswinkel hat seinen Scheitelpunkt auf dem Kreisumfang und seine Seiten sind Sekanten.
Er misst die Hälfte des Bogens, den er umspannt.
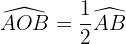
3 Sehnentangentenwinkel
Der Scheitelpunkt des Sehnentangentenwinkels liegt auf dem Kreisumfang, eine Seite ist eine Sekante und die andere eine Tangente an den Kreisumfang.
Er misst die Hälfte des Bogens, den er umspannt.
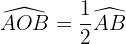
4 Innenwinkel
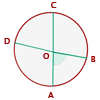
Sein Scheitelpunkt liegt innerhalb des Kreisumfangs und seine Seiten sind Sekanten.
Er misst die Hälfte der Summe der Maße der Bögen, die seine Seiten umspannen, und der Verlängerungen seiner Seiten.
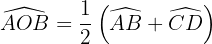
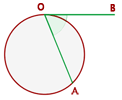
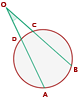
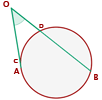
5 Außenwinkel
Sein Scheitelpunkt ist ein Punkt außerhalb des Kreisumfangs. Die Seiten seiner Winkel sind entweder Sekanten oder eine Tangente und eine Sekante oder Tangenten:
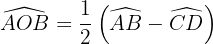

Fläche und Länge des Kreisumfangs
Länge eines Kreisumfangs
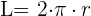
Beispiel:
Berechne den Umfang eines Rades, das einen Durchmesser von 180 cm hat.
L = 2 · π · r
r= 1/2 · D = 180:2=90
L= 2 · π · 90 = 565,47 cm
Wir haben die Formel 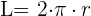
Außerdem ist 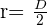 , wobei
, wobei  der Durchmesser ist. Somit
der Durchmesser ist. Somit
Mit dem Radius können wir nun die Formel anwenden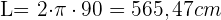
Länge eines Kreisbogens
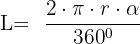
Beispiel:
Die Arme einer Schaukel sind 1,80 m lang und können einen maximalen Winkel von 146° beschreiben. Berechne den Raum, den der Sitz der Schaukel einnimmt, wenn der beschriebene Winkel der Schaukel maximal ist.
Wir haben 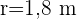 und
und  . Nun wenden wir unsere Formel an:
. Nun wenden wir unsere Formel an: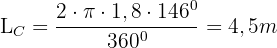
Sternpolygone
Ein regelmäßiger Stern wird konstruiert, indem die nicht aufeinanderfolgenden Eckpunkte eines regelmäßigen konvexen Vielecks fortlaufend verbunden werden.
Sie werden mit p/q angegeben, wobei p die Anzahl der Eckpunkte des regelmäßigen konvexen Vielecks ist und q der Sprung zwischen den Eckpunkten ist.
p/q muss ein nicht kürzbarer Bruch sein.
Das Vieleck p/q ist dasselbe wie p/(p-q), da das sternförmige Vieleck, das durch die Verbindung von Eckpunkten in einer Richtung und in der entgegengesetzten Richtung entsteht, dasselbe ist.
Umfang eines Vielecks: Die Summe der Längen der Seiten eines Vielecks.
Fläche: Sie ist das Maß für den Bereich oder die Fläche, die von einer ebenen Figur umschlossen wird.
1 Fläche eines Quadrats:

Diagonale
Umfang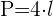
Fläche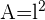
2 Fläche eines Rechtecks:
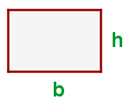
Diagonale
Umfang
Fläche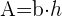
3 Fläche einer Raute:
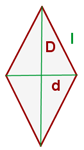
Umfang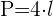
Fläche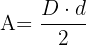
4 Fläche eines Parallelogramms:
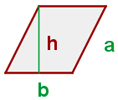
Umfang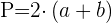
Fläche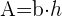
5 Fläche eines Trapezes:
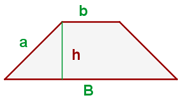
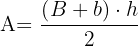
6 Fläche eines Dreiecks:
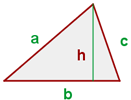
Umfang
Fläche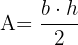
7 Fläche eines Vielecks:
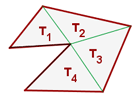
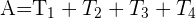 ,
,
wobei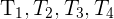 die Flächen der Dreiecke sind.
die Flächen der Dreiecke sind.
Den Flächeninhalt erhält man, indem man das Vieleck in Dreiecke zerlegt und die Flächeninhalte dieser Dreiecke addiert.
Beispiel:
Berechne die Fläche des folgenden Vielecks:
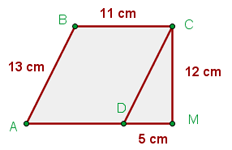
Wir haben 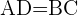 ;
; 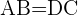 ist somit ein Parallelogramm und zur Berechnung seiner Fläche verwenden wir folgenden Ausdruck:
ist somit ein Parallelogramm und zur Berechnung seiner Fläche verwenden wir folgenden Ausdruck: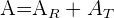 ,
,
wobei 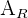 die Fläche des Rechtecks und
die Fläche des Rechtecks und 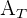 die Fläche des Dreiecks ist.
die Fläche des Dreiecks ist.
Wenn also die Höhe  , die Basis des Rechtecks
, die Basis des Rechtecks  und die Basis des Dreiecks
und die Basis des Dreiecks  ist, wenden wir folgende Formeln an
ist, wenden wir folgende Formeln an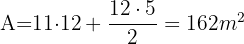
8 Fläche eines regelmäßigen Vielecks:
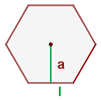
Umfang
Fläche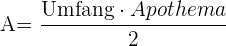
Beispiel:
Berechne die Fläche eines regelmäßigen Fünfecks mit einer Seitenlänge von 6 cm.
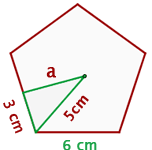
Wie aus der Abbildung ersichtlich ist, müssen wir das Apothema mithilfe des Satzes des Pythagoras berechnen.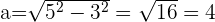
Da 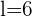 und es sich um ein Fünfeck handelt, ist der Umfang
und es sich um ein Fünfeck handelt, ist der Umfang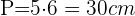
Schließlich ist die Fläche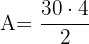
Berechne die Fläche eines regelmäßigen Sechsecks, das in einen Kreis mit einem Radius von 4 cm eingeschrieben ist.
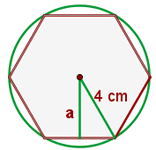
Wir haben 
Wie aus der Abbildung ersichtlich ist, müssen wir das Apothema mithilfe des Satzes des Pythagoras berechnen.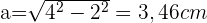
Da 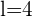 und es ein Sechseck ist, beträgt der Umfang
und es ein Sechseck ist, beträgt der Umfang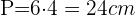
Somit ist die Fläche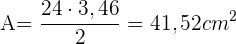
Mit KI zusammenfassen:












