Kapitel
Elemente eines Vielecks
Ein Vieleck ist der Bereich der Ebene, der durch drei oder mehr Segmente begrenzt wird. Die Elemente eines Vielecks sind:
1 Seiten: Die Segmente, die es begrenzen.
2 Eckpunkte: Punkte, an denen die Seiten zusammentreffen.
3 Innenwinkel: Werden durch zwei aufeinanderfolgende Seiten bestimmt.
Eine interessante Eigenschaft der Innenwinkel eines Vielecks mit 
Seiten besteht darin, dass man, wenn man im Inneren des Vielecks Dreiecke bildet, die Summe aller Innenwinkel dieser Dreiecke durch folgende Formel berechnen kann
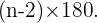
Bei dieser Formel steht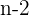 
für die Anzahl der Dreiecke, die wir bilden können, und wir fügen den Faktor 
hinzu, da wir wissen, dass dies die Summe der Innenwinkel eines Dreiecks ist.
4 Diagonale: Ein beliebiges Segment, das durch zwei nicht aufeinanderfolgende Eckpunkte bestimmt wird.
Die Anzahl der Diagonalen eines Vielecks mit un polígono de Seiten kann mit folgender Formel berechnet werden
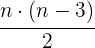
Es gibt mehrere Möglichkeiten, Vielecke zu klassifizieren. Die erste, die wir untersuchen werden, ist die Klassifizierung, die sich aus der Berücksichtigung der Anzahl der Seiten ergibt.
Klassifizierung von Vielecken nach Anzahl der Seiten
Dreiecke
Haben 3 Seiten.
Vierecke
Haben 4 Seiten.
Fünfeck
Haben 5 Seiten.
Sechsecke
Haben 6 Seiten.
Siebenecke
Haben 7 Seiten.
Achtecke
Haben 8 Seiten.
Neunecke
Haben 9 Seiten.
Zehnecke
Haben 10 Seiten.
Elfecke
Haben 11 Seiten.
Zwölfecke
Haben 12 Seiten.
Dreizehnecke
Haben 13 Seiten.
Vierzehnecke
Haben 14 Seiten.
Fünfzehnecke
Haben 15 Seiten.
Sechzehnecke
Haben 16 Seiten.
Siebzehnecke
Haben 17 Seiten.
Achtzehnecke
Haben 18 Seiten.
Neunzehnecke
Haben 19 Seiten.
Zwanzigecke
Haben 20 Seiten.
Klassifizierung von Vielecken nach ihren Winkeln
Die Klassifizierung von Vielecken nach ihren Winkeln bezieht sich auf die Größe der Innenwinkel.
Konvex
Konvexe Vielecke sind solche, bei denen das Maß jedes Innenwinkels kleiner als 180° ist und alle ihre Diagonalen innen liegen.
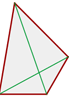
Konkav
Ein Vieleck wird als konvex bezeichnet, wenn das Maß eines Innenwinkels größer als 180° ist oder wenn eine der Diagonalen außen liegt.
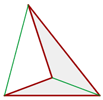
Regelmäßige Vielecke
Ein regelmäßiges Vieleck ist ein Vieleck, dessen Innenwinkel gleich sind und dessen Seiten gleich lang sind.
Elemente eines regelmäßigen Vielecks
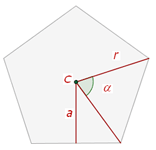
1 Mittelpunkt: Der innere Punkt, der von jedem Punkt gleich weit entfernt ist.
2 Radius: Segment, das vom Mittelpunkt zu jedem Punkt verläuft.
3 Apothema: Abstand vom Mittelpunkt zum Mittelpunkt einer Seite.
4 Mittelpunktswinkel: Winkel, der von zwei aufeinanderfolgenden Radien gebildet wird.
Für ein regelmäßiges Vieleck mit Seiten gelten folgende Formeln
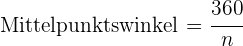
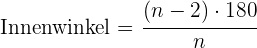
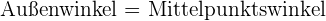
Eingeschriebene Vielecke
Ein Vieleck ist in einen Kreis eingeschrieben, wenn alle seine Eckpunkte in ihm enthalten sind.
Umkreis
Wir nennen den Umkreis den einzigen Kreis, der alle Eckpunkte des Vielecks berührt, dessen Mittelpunkt von allen Eckpunkten gleich weit entfernt ist und dessen Radius mit dem Radius des Vielecks übereinstimmt.
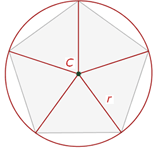
Inkreis
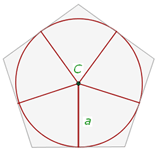
Als Inkreis bezeichnen wir den einzigen Kreis, der den Mittelpunkt jeder Seite des Vielecks berührt, dessen Mittelpunkt von allen Seiten gleich weit entfernt ist und dessen Radius mit der Apothema des Vielecks übereinstimmt.
Arten von Dreiecken
Wie bereits zu Beginn des Artikels erwähnt, ist ein Dreieck ein Vieleck mit drei Seiten. Für diese Art von Vielecken gelten die folgenden Aussagen.
1 Eine Seite eines Dreiecks ist kleiner als die Summe der beiden anderen und größer als deren Differenz.
2 Die Summe der Innenwinkel eines Dreiecks beträgt 180°.
3 Der Wert eines Außenwinkels ist gleich der Summe der beiden nicht benachbarten Innenwinkel.
Wir können Dreiecke nach dem Verhältnis ihrer Seiten zueinander klassifizieren.
Gleichseitiges Dreieck
Ein gleichseitiges Dreieck ist ein Dreieck, dessen drei Seiten gleich lang sind.
Gleichschenkliges Dreieck
Ein Dreieck mit nur zwei gleich langen Seiten wird als gleichseitiges Dreieck bezeichnet.
Unregelmäßiges Dreieck
Ein unregelmäßiges Dreieck ist ein Dreieck, bei dem alle Seiten unterschiedlich lang sind.
Die folgende Klassifizierung wird durch ihre Winkel definiert.
Spitzwinkliges Dreieck
Dreieck mit drei spitzen Winkeln.
Rechtwinkliges Dreieck
Dreieck mit rechtem Winkel. Bei dieser Art von Dreieck gilt der Satz des Pythagoras und in diesem Zusammenhang ist die Hypotenuse die längere Seite, während die kürzeren Seiten die Katheten sind.
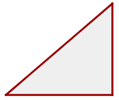
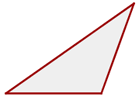
Stumpfwinkliges Dreieck
Ein Dreieck mit mindestens einem stumpfen Winkel wird als stumpfwinklig bezeichnet.
Wichtige geometrische Stellen im Dreieck
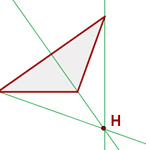
Höhen eines Dreiecks
Jede der senkrechten Geraden, die von einem Eckpunkt zur gegenüberliegenden Seite (oder ihrer Verlängerung) verläuft, wird als Höhe bezeichnet.
Höhenschnittpunkt
Schnittpunkt der drei Höhen.
Seitenhalbierende eines Dreiecks
Die Seitenhalbierende ist jede der Geraden, die den Mittelpunkt einer Seite mit dem gegenüberliegenden Eckpunkt verbindet.
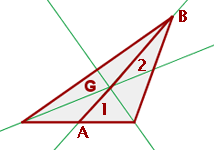
Schwerpunkt
Der Schnittpunkt der drei Seitenhalbierenden wird als Schwerpunkt bezeichnet. Dieser Punkt teilt jede Seitenhalbierende in zwei Segmente mit der folgenden Eigenschaft: Das Segment, das den Schwerpunkt mit dem Eckpunkt verbindet, ist doppelt so lang wie das Segment, das den Schwerpunkt mit dem Mittelpunkt der gegenüberliegenden Seite verbindet. Im Zusammenhang mit der nachstehenden Abbildung bedeutet dies Folgendes
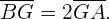
Mittelsenkrechte eines Dreiecks
Die Mittelsenkrechte ist jede der senkrechten Geraden, die zu einer Seite durch ihren Mittelpunkt gezogen wird.
Umkreismittelpunkt
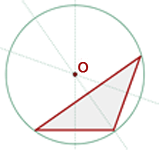
Er ist der Schnittpunkt der drei Mittelsenkrechten. Er ist außerdem der Mittelpunkt eines Kreises, der das Dreieck umschreibt.
Winkelhalbierende eines Dreiecks
Die Winkelhalbierende ist jede der Geraden, die einen Innenwinkel in zwei gleiche Winkel teilt.
Inkreismittelpunkt
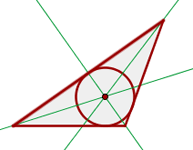
Er ist der Schnittpunkt der drei Winkelhalbierenden und der Mittelpunkt eines in das Dreieck eingeschriebenen Kreises.
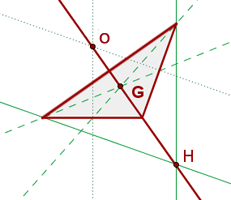
Eulersche Gerade
Bei einem nicht gleichseitigen Dreieck sind der Höhenschnittpunkt, der Schwerpunkt und der Umkreismittelpunkt kollinear; Das heißt, es gibt eine Gerade, zu der alle drei Punkte gehören. Diese Gerade wird als Eulersche Gerade bezeichnet.
Klassifizierung von Vierecken
Als Vierecke bezeichnet man Vielecke, die vier Seiten haben. Für diese Vielecke gilt, dass die Summe ihrer Innenwinkel 360° ist.
Parallelogramme
Bei diesen Vielecken handelt es sich um Vierecke, deren Seiten paarweise parallel sind und die wie folgt klassifiziert werden:
Quadrat
Vier gleiche Seiten und 4 rechte Innenwinkel.
Rechteck
Zwei gleiche Seiten und 4 rechte Innenwinkel.
Raute
Hat 4 gleiche Seiten.
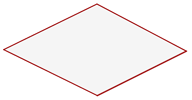
Parallelogramm
Jeweils 2 Seiten sind gleich.
Trapeze
Vierecke, die nur zwei parallele Seiten haben. Diese werden wie folgt klassifiziert:
Rechtwinkliges Trapez
Trapez mit einem rechten Innenwinkel.
Gleichschenkliges Trapez
Trapez mit zwei gleichen, nicht parallelen Seiten.
Unregelmäßiges Trapez
Es hat keine gleichen Seiten oder rechten Winkel.
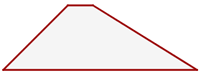
Trapezoid
Vierecke, die weder gleiche noch parallele Seiten haben.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
