Kapitel
In diesem Artikel erfährst du, wie du das Apothema von regelmäßigen zweidimensionalen Vielecken, sowie von Pyramiden und anderen dreidimensionalen geometrischen Figuren berechnest.
Erinnere dich daran, dass das Apothema eines regelmäßigen Vielecks der Abstand zwischen seinem Mittelpunkt und dem Mittelpunkt einer Seite ist.

Apothema eines gleichseitigen Dreiecks
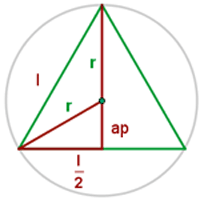
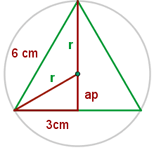
Finde zuerst den Wert einer Seite des Dreiecks in Bezug auf den Radius des Kreises, der sie umschreibt. Beachte in der Abbildung, dass die Höhe gleich des Apothemas plus dem Radius ist, d. h

Außerdem erhältst du unter Verwendung vom Satz des Pythagoras, dass
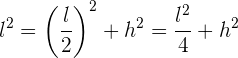
dies mit Hilfe des rechtwinkligen Dreiecks, das durch die Seite, die Höhe und die Hälfte der Grundseite (die gleich der Hälfte der Seite ist) gebildet wird. Wenn du nun 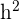 verrechnest, erhältst du
verrechnest, erhältst du

Durch Lösen der Wurzel
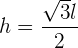
Wenn du 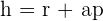 einsetzt, erhältst du
einsetzt, erhältst du
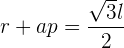
oder auch
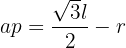
Quadriere
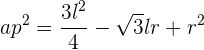
Beachte außerdem, dass du ein weiteres rechtwinkliges Dreieck hast, das durch das Apothema, den Radius und die Hälfte einer Seite gebildet wird. Aus diesem rechtwinkligen Dreieck folgt
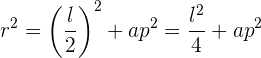
nach Verrechnung des Apothemas zum Quadrat ergibt sich
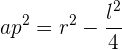
Gleiche nun die beiden erhaltenen Ergebnisse für 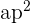 aus und löse eine Seite auf, d. h
aus und löse eine Seite auf, d. h
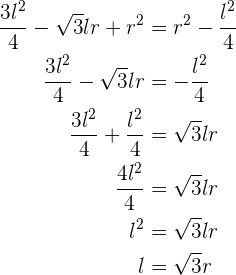
dies bedeutet auch, dass

Rationalisiere den Nenner
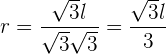
Setze diesen Wert in die Gleichung 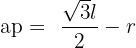 ein, die du zuvor erhalten hast
ein, die du zuvor erhalten hast
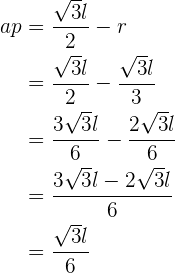
Somit ist das Apothema gleich 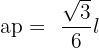 .
.
Beachte, dass du hier sowohl den Radius als auch das Apothema in Bezug auf die Seite des Dreiecks erhalten hast. Betrachte jetzt das folgende Beispiel
Berechne das Apothema eines gleichseitigen Dreiecks der Seite 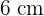 .
.
Du weißt, dass die Formel folgendermaßen lautet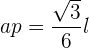
wenn du den Wert der Seite substituierst, erhältst du
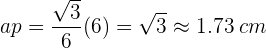
Apothema eines Quadrats
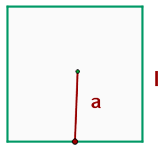
Das Apothema eines Quadrats ist gleich der Hälfte der Seite, also:
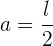
Betrachte das folgende Beispiel
Berechne das Apothema eines Quadrats mit 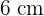 Seitenlänge.
Seitenlänge.
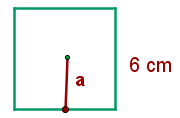
Du weißt, dass die Formel folgendermaßen lautet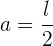
wenn du den Wert der Seite substituierst, erhältst du
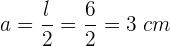
Apothema eines Fünfecks
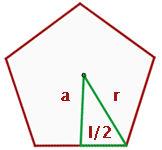
Erinnere dich zunächst daran, dass der zentrale Winkel eines Fünfecks im Bogenmaß 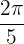 beschrieben wird. Daher ist der Winkel zwischen dem Scheitelpunkt und dem Radius die Hälfte, also
beschrieben wird. Daher ist der Winkel zwischen dem Scheitelpunkt und dem Radius die Hälfte, also 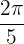 . Der Sinus dieses Winkels ist die Gegenkathete der Hypotenuse, also
. Der Sinus dieses Winkels ist die Gegenkathete der Hypotenuse, also
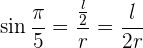
nach Abzug von  ergibt sich, dass
ergibt sich, dass
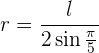
dann kannst du den Radius direkt von einer Seite erhalten, da du den Sinus direkt mit dem Taschenrechner berechnen kannst.
Mit Hilfe des Satzes von Pythagoras ergibt sich folgendes:
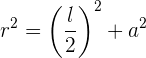
durch Auflösen des Apothemas und Ziehen der Wurzel
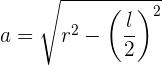
diese Formel kann direkt verwendet werden, wenn du bereits den Wert des Radius und einer Seite hast. Wenn du nur den Wert einer Seite hast, dann ersetzt du den Wert des Radius in Bezug auf die Seite
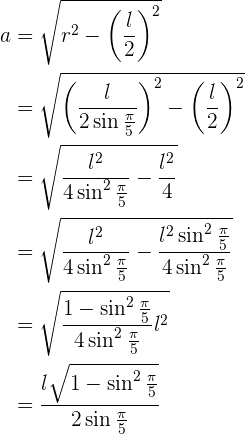
Beachte, dass hier das Apothema nur von der Seite abhängt - du musst aber mehr Operationen durchführen. Daher ist es bequemer, die Seite und den Radius zu haben.
Betrachte das folgende Beispiel
Berechne das Apothema eines Fünfecks mit 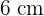 Seitenlänge und
Seitenlänge und 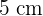 Radius.
Radius.
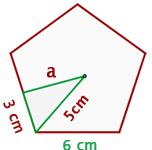
Du weißt, dass die Formel folgendermaßen lautet: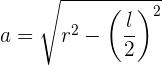
wenn du den Wert der Seite und des Radius einsetzt, erhältst du
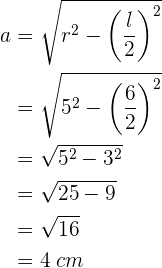
Apothema eines Sechsecks
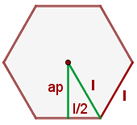
Erinnere dich zunächst daran, dass der zentrale Winkel eines Fünfecks im Bogenmaß 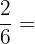 beschrieben wird. Daher ist der Winkel zwischen dem Apothema und dem Radius halb so groß, also
beschrieben wird. Daher ist der Winkel zwischen dem Apothema und dem Radius halb so groß, also  . Der Sinus dieses Winkels ist die Gegenkathete der Hypotenuse, also
. Der Sinus dieses Winkels ist die Gegenkathete der Hypotenuse, also
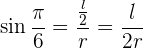
Du musst aber auch
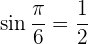
woraus folgt, dass
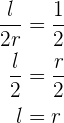
dann weißt du, dass in einem Sechseck der Radius das Gleiche misst wie eine Seite.
Mit Hilfe vom Satz des Pythagoras ergibt sich, dass
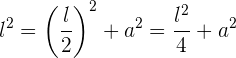
oder auch

Durch Ziehen der Wurzel
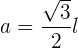
Betrachte das folgende Beispiel
Berechne das Apothema eines Fünfecks mit  Seitenlänge.
Seitenlänge.
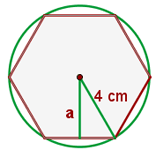
Du weißt, dass deine Formel folgendermaßen lautet: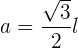
wenn du den Wert der Seite und des Radius einsetzt, erhältst du
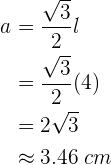
Apothema einer Pyramide
Das seitliche Apothema einer regelmäßigen Pyramide ist die Höhe einer beliebigen ihrer Seitenflächen.
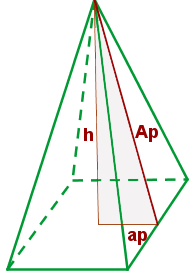
Berechne das seitliche Apothema der Pyramide (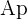 ), wenn du die Höhe (
), wenn du die Höhe ( ) und das Apothema der Grundseite (
) und das Apothema der Grundseite ( ) kennst und wende den Satz des Pythagoras im schraffierten Dreieck an. Daher ist das Quadrat des seitlichen Apothemas gegeben durch
) kennst und wende den Satz des Pythagoras im schraffierten Dreieck an. Daher ist das Quadrat des seitlichen Apothemas gegeben durch

oder, das seitliche Apothema ist gegeben durch
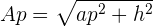
Apothema eines Pyramidenstamms
Ein regelmäßiger Pyramidenstamm wird durch zwei Grundflächen gebildet, die ähnliche regelmäßige Vielecke sind, und mehrere Seitenflächen, die gleichschenklige Trapeze sind. Die Apothemata sind die Höhen dieser Trapeze.
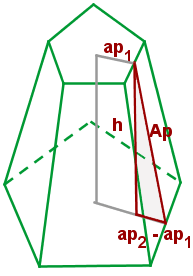
Du berechnest das seitliche Apothema des Pyramidenstamms (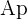 ) bei Kenntnis der Höhe (
) bei Kenntnis der Höhe ( ), das Apothema der Grundfläche (
), das Apothema der Grundfläche (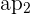 ) und das Apothema der Nebenfläche (
) und das Apothema der Nebenfläche (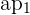 ) unter Anwendung vom Satz des Pythagoras im schattierten Dreieck im Bild.
) unter Anwendung vom Satz des Pythagoras im schattierten Dreieck im Bild.
Beachte, dass in diesem Dreieck eine der Katheten die Höhe ist, während die andere die Differenz aus dem Apothema der Grundfläche minus dem Apothema der Nebenfläche ist. Daher wäre das Quadrat des seitlichen Apothemas
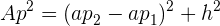
oder, das seitliche Apothema wäre
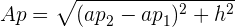
Mit KI zusammenfassen:













