Kapitel
- Definition eines Dreiecks
- Eigenschaften von Dreiecken
- Gleiche Dreiecke
- Klassifizierung von Dreiecken nach ihren Seiten und Umfangsformeln
- Klassifizierung von Dreiecken nach ihren Winkeln
- Klassifizierung von Dreiecken nach ihren Winkeln
- Wichtige Elemente in Dreiecken
- Flächeninhalt eines Dreiecks
- Sätze und Formeln

Definition eines Dreiecks
Ein Dreieck ist ein Polygon, das durch drei Liniensegmente, genannt Seiten, oder durch drei nicht ausgerichtete Punkte, genannt Scheitelpunkte, bestimmt wird.
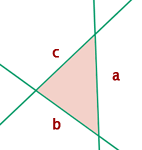
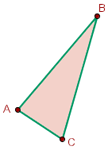
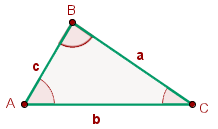
Die Eckpunkte eines Dreiecks werden in Großbuchstaben geschrieben.
Die Seiten eines Dreiecks werden kleingeschrieben, mit den gleichen Buchstaben wie die gegenüberliegenden Eckpunkte.
Die Winkel eines Dreiecks werden auf die gleiche Weise geschrieben wie die Scheitelpunkte.
Eigenschaften von Dreiecken
1 Eine Seite eines Dreiecks ist kleiner als die Summe der beiden anderen und größer als deren Differenz.
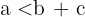
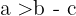
2 Die Summe der drei Winkel eines Dreiecks beträgt  .
.
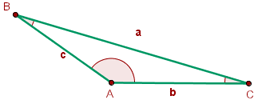
3 In einem Dreieck gilt: Je größer die Seite, desto größer der Winkel.
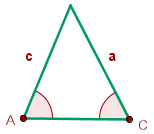
4 Der Wert eines Außenwinkels ist gleich der Summe der beiden nicht benachbarten Innenwinkel. Wenn ein Dreieck zwei gleiche Seiten hat, sind auch seine gegenüberliegenden Winkel gleich.
Gleiche Dreiecke
1 Zwei Dreiecke sind gleich, wenn sie eine Seite haben und ihre beiden benachbarten Winkel gleich sind.
2 Zwei Dreiecke sind gleich, wenn sie zwei gleiche Seiten und einen eingeschlossenen Winkel haben.
3 Zwei Dreiecke sind gleich, wenn sie drei gleiche Seiten haben.
Klassifizierung von Dreiecken nach ihren Seiten und Umfangsformeln
| Gleichseitiges Dreieck | Gleichschenkliges Dreieck | Ungleichseitiges Dreieck |
|---|---|---|
| U = 3 x l | U = 2 x l + b | U = a + b + c |
 |  |  |
Klassifizierung von Dreiecken nach ihren Winkeln
Spitzwinkliges Dreieck
Es hat drei spitzen Winkel
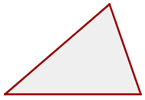
Rechtwinkliges Dreieck
Es hat einen rechten Winkel.
Die größere Seite ist die Hypotenuse.
Die Nebenseiten sind die Katheten.
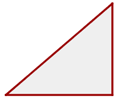
Stumpfwinkliges Dreieck
Es hat einen stumpfen Winkel.
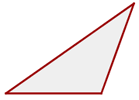
Klassifizierung von Dreiecken nach ihren Winkeln
Gleichseitiges Dreieck: ein Dreieck mit drei gleichen Seiten

Gleichschenkliges Dreieck: ein Dreieck mit zwei gleichen Seiten

Unregelmäßiges Dreieck: ein Dreieck mit drei ungleichen Seiten
Wichtige Elemente in Dreiecken
Höhen eines Dreiecks:
Die Höhe ist jede der senkrechten Linien, die von einem Scheitelpunkt zur gegenüberliegenden Seite (oder deren Verlängerung) gezogen werden.
Höhenschnittpunkt
Er ist der Schnittpunkt der drei Höhen.
Mediane eines Dreiecks
Der Median ist jede der Geraden, die den Mittelpunkt einer Seite mit dem gegenüberliegenden Scheitelpunkt verbindet.
Schwerpunkt
Er ist der Schnittpunkt der drei Seitenhalbierenden.
Der Schwerpunkt teilt jede Seitenhalbierende in zwei Segmente, wobei das Segment, das den Schwerpunkt mit dem Scheitelpunkt verbindet, doppelt so lang ist wie das Segment, das den Schwerpunkt mit dem Mittelpunkt der gegenüberliegenden Seite verbindet.
Mittelsenkrechte eines Dreiecks
Die Mittelsenkrechte ist jede der senkrechten Linien, die zu einer Seite durch ihren Mittelpunkt gezogen wird.
Umkreis
Er ist der Schnittpunkt der drei Mittelsenkrechten.
Er ist der Mittelpunkt eines Kreises, der das Dreieck umschreibt.
Winkelhalbierende eines Dreiecks
Die Winkelhalbierende ist jede der Geraden, die einen Winkel in zwei gleiche Winkel teilt.
Inkreis
Er ist der Schnittpunkt der drei Winkelhalbierenden.
Er ist der Mittelpunkt eines in das Dreieck eingeschriebenen Kreises.
Eulersche Gerade
Der Höhenschnittpunkt, das Baryzentrum und der Umkreis eines unregelmäßigen Dreiecks sind zueinander ausgerichtet, d.h. sie gehören zur selben Linie, die Eulersche Linie genannt wird.
Flächeninhalt eines Dreiecks
Der Flächeninhalt eines Dreiecks ist gleich der Hälfte des Produkts aus seiner Grundseite und seiner Höhe.
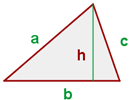

Beispiel: Finde den Flächeninhalt des folgenden Dreiecks
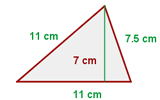
Die Grundseite beträgt  und die Höhe
und die Höhe  , also ist der Flächeninhalt
, also ist der Flächeninhalt
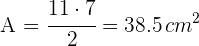
Flächeninhalt eines rechtwinkligen Dreiecks
Der Flächeninhalt eines rechtwinkligen Dreiecks ist gleich der Hälfte des Produkts der Schenkel.
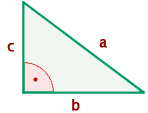

Beispiel: Finde den Flächeninhalt des rechtwinkligen Dreiecks, dessen Schenkel  und
und  messen.
messen.
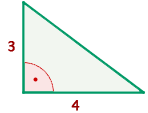
Die Schenkel sind  und
und  lang, also ist ihre Fläche
lang, also ist ihre Fläche
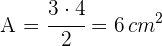
Halbumfang
Der Halbumfang eines Dreiecks ist gleich der Summe seiner Seiten geteilt durch 2. Er wird mit dem Buchstaben  bezeichnet
bezeichnet

Zwei Seiten und deren Winkel sind bekannt
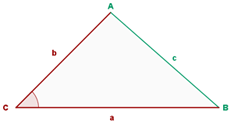

Kreisumfang eines Dreiecks
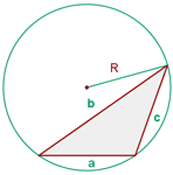

wobei  der Radius des umschriebenen Kreises ist
der Radius des umschriebenen Kreises ist
In ein Dreieck eingeschriebener Kreisumfang
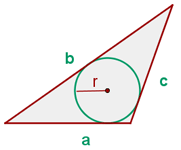
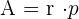
wobei  der Radius des eingeschriebenen Kreises ist
der Radius des eingeschriebenen Kreises ist
Sätze und Formeln
Kathetensatz
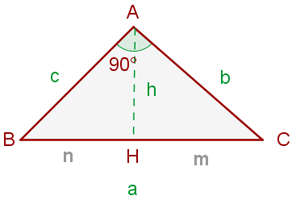
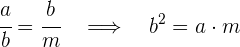

Höhensatz
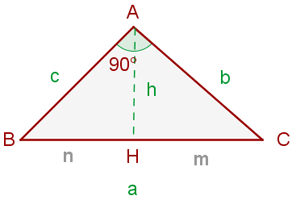

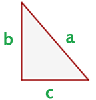
Satz des Pythagoras

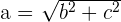
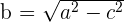
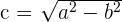
Satz des Heron
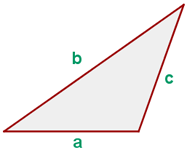

wobei  der Halbumfang ist.
der Halbumfang ist.
Beispiel: Finde den Flächeninhalt des Dreiecks, dessen Seiten 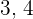 und
und  messen.
messen.
Berechne den Halbumfang
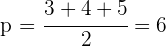
Wende den Satz des Heron an
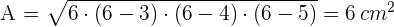
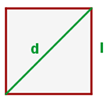
Diagonale des Quadrats
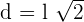
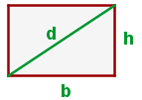
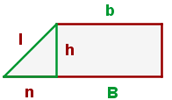
Diagonale des Rechtecks

Schräge Seite eines rechteckigen Trapezes

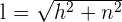
Höhe eines gleichschenkligen Trapezes
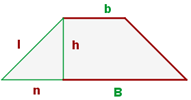


Höhe eines gleichseitigen Dreiecks
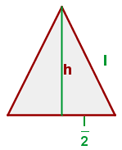
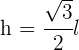
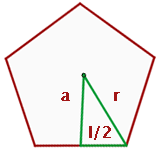
Apothema eines regelmäßigen Vielecks

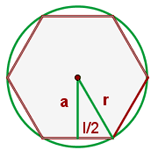
Apothema eines eingeschriebenen Sechsecks

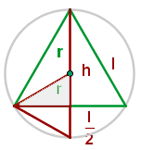
Seite eines eingeschriebenen gleichseitigen Dreiecks

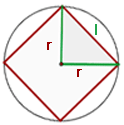
Seite eines eingeschriebenen Quadrats
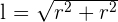
Mit KI zusammenfassen:













