
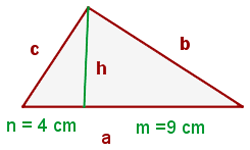
Kathetensatz
In jedem rechtwinkligen Dreieck ist eine Kathete zur Hälfte proportional zur Hypotenuse und ihrer Projektion auf diese.
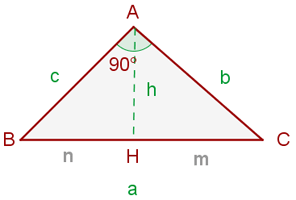
 ist die Hypotenuse
ist die Hypotenuse und
und  sind die Katheten
sind die Katheten ist die Projektion der Kathete
ist die Projektion der Kathete  auf die Hypotenuse
auf die Hypotenuse ist die Projektion der Kathete
ist die Projektion der Kathete  auf die Hypotenuse
auf die Hypotenuse


Beispiel
Die Hypotenuse eines rechtwinkligen Dreiecks misst  cm und die Projektion einer Kathete auf sie
cm und die Projektion einer Kathete auf sie 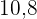 cm. Ermittle die andere Kathete.
cm. Ermittle die andere Kathete.


Höhensatz
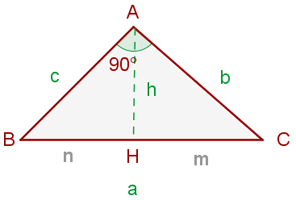
In einem rechtwinkligen Dreieck ist die Höhe in Bezug auf die Hypotenuse halb proportional zwischen den beiden Segmenten, die die Hypotenuse unterteilen.

Beispiel
In einem rechtwinkligen Dreieck messen die Projektionen der Katheten auf die Hypotenuse  und
und  Zentimeter. Berechne die Höhe bezogen auf die Hypotenuse.
Zentimeter. Berechne die Höhe bezogen auf die Hypotenuse.


Satz des Pythagoras
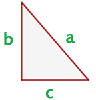
In allen rechtwinkligen Dreiecken ist die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates.
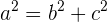
Anwendungsbeispiele für den Satz des Pythagoras
Berechne unter Kenntnis der beiden Katheten die Hypotenuse

Beispiel:
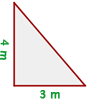
1 Die Katheten eines rechtwinkligen Dreiecks messen  m bzw.
m bzw.  m. Wie lang ist die Hypotenuse?
m. Wie lang ist die Hypotenuse?

Du kennst bereits die Hypotenuse und eine Kathete und berechnest nun die andere Kathete.

2 Die Hypotenuse eines rechtwinkligen Dreiecks misst  m und eine seiner Katheten
m und eine seiner Katheten  m. Wie viel misst die andere Kathete?
m. Wie viel misst die andere Kathete?

Du kennst bereits zwei Seiten. Überprüfe nun, ob es rechtwinklig ist
Um rechtwinklig zu sein, muss das Quadrat der größeren Seite gleich der Summe der Quadrate der beiden kleineren Seiten sein.
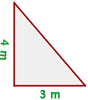
3 Bestimme, ob das Dreieck rechtwinklig ist.
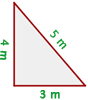

Berechne die Diagonale des Quadrats
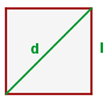
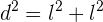
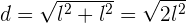
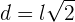
Berechne die Diagonale des Rechtecks
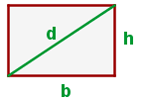
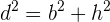
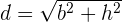
Berechne die schräge Seite des rechteckigen Trapezes
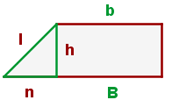
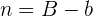
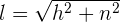
Berechne die Höhe des gleichschenkligen Trapezes
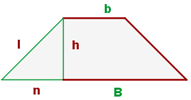
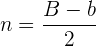
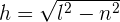
Berechne die Höhe des gleichseitigen Dreiecks
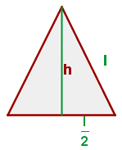


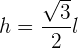
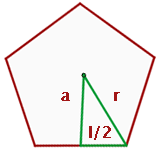
Berechne das Apothema eines regelmäßigen Fünfecks
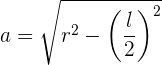
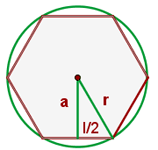
Berechne das Apothema eines eingeschriebenen Sechsecks
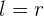
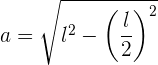
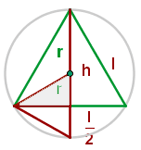
Berechne die Seite eines eingeschriebenen gleichseitigen Dreieckes



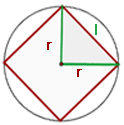
Berechne die Seite eines eingeschriebenen Quadrats
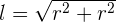
Mit KI zusammenfassen:













