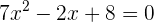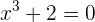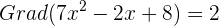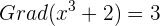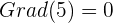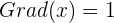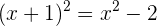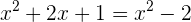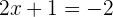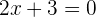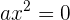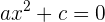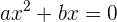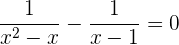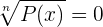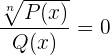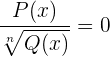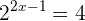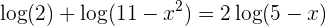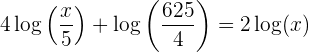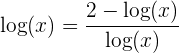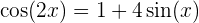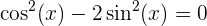Kapitel
Polynomgleichungen haben die Form 
, wobei 
ein Polynom ist.
Zum Beispiel:
Der Grad einer Gleichung ist der höchste Grad der Grade der Monome, die das Polynom bilden.
Zum Beispiel:
Arten von Polynomgleichungen:
1Gleichungen 1. Grades oder lineare Gleichungen
Diese Gleichungen haben die Form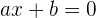 
, wobei 
, oder es handelt sich um eine beliebige andere Gleichung, die durch das Durchführen von Rechenschritten, Umstellen der Terme oder durch Vereinfachung diesen Ausdruck annehmen.
2 Gleichungen 2. Grades oder quadratische Gleichungen
Diese Gleichungen haben die Form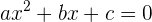 
, wobei . Wenn hierbei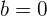 
oder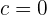 
, heißen diese Gleichungen unvollständige quadratische Gleichungen.
3Gleichungen 3. Grades
Gleichungen vom Typ 
, mit .
4Gleichungen 4. Grades
Dies sind Gleichungen vom Typ 
mit .
5Biquadratische Gleichungen
Hierbei handelt es sich um Gleichungen 4. Grades, bei denen keine Terme mit ungeradem Grad vorkommen 
, wobei .
6Gleichungen vom Grad 
Im Allgemeinen haben Gleichungen vom Grad n folgende Form: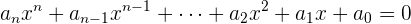 
Rationale Polynomgleichungen
Rationale Polynomgleichungen haben folgende Form
,
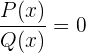wobei und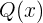 
Polynome sind.
Zum Beispiel:
Irrationale Polynomgleichungen
Irrationale Gleichungen sind Gleichungen, bei denen mindestens ein Polynom unter dem Radikal steht.
Zum Beispiel:
Gleichungen ohne Polynome
1Exponentialgleichungen
Dabei handelt es sich um Gleichungen, bei denen die Unbekannte im Exponenten steht, zum Beispiel:
2Logarithmusgleichungen
Hierbei handelt es sich um Gleichungen, bei denen die Variable im Numerus des Logarithmus steht. Zum Beispiel:
3Trigonometrische Gleichungen
Dies sind Gleichungen, bei denen die zu bestimmende Variable im Argument von tigonometrischen Funktionen vorkommt. Da diese periodisch sind, gibt es im Allgemeinen unendlich viele Lösungen, zum Beispiel:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
