1Löse die folgenden Gleichungen:

1 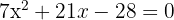
Diese können mit der abc-Formel oder durch Faktorisierung gelöst werden. Wir wenden die Faktorisierung an:
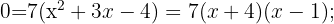

2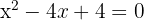
Wir faktorisieren:
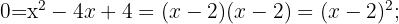
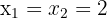
3
Wir faktorisieren:


4
Wir faktorisieren:


2Löse die folgenden Gleichungen: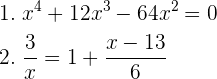
1 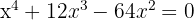
Wir faktorisieren:

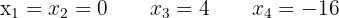
2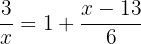
Das zweite Glied schreiben wir mit einem gemeinsamen Nenner und zwischen den einzelnen Gliedern wird abwechselnd ein Produkt aus den Nennern gebildet. Im Anschluss faktorisieren wir:
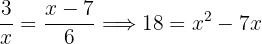


3Löse die folgenden Gleichungen:
1
Wir faktorisieren:
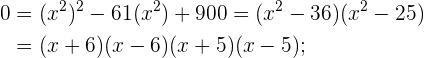

2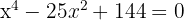
Wir faktorisieren:
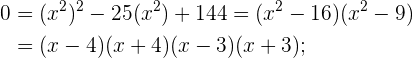

4Löse die folgenden Gleichungen: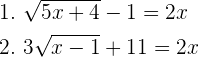
1
Als Erstes sehen wir uns die Wurzel der Gleichung an. Danach quadrieren wir beide Glieder und führen alle nötigen Berechnungen durch.

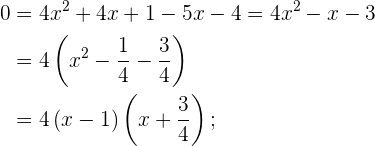

2 
Wir rechnen die Wurzel der Gleichung aus. Danach quadrieren wir beide Glieder und führen alle nötigen Berechnungen durch. Wir lösen mit der abc-Formel:

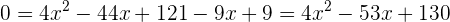

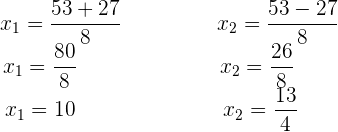
5Bestimme die Nullstellen von: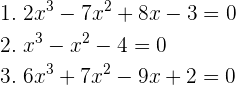
1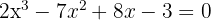
Wir wenden das Horner-Schema an, da es sich um eine Gleichung 3. Grades handelt. Die Divisoren von  sind
sind 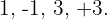 Somit:
Somit:
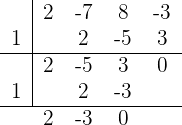
Die Faktorisierung ist also 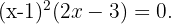 Deshalb:
Deshalb:
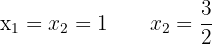
2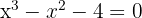
Wir wenden das Horner-Schema an, da es sich um eine Gleichung 3. Grades handelt. Die Divisoren von  sind
sind 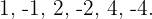 Somit:
Somit:
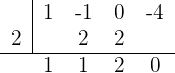
Die Faktorisierung ist also 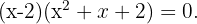 Bei der Berechnung der Diskriminante des Trinoms stellen wir fest, dass das Trinom keine Nullstellen hat, da das Ergebnis negativ ist. Es gibt also nur eine Lösung.
Bei der Berechnung der Diskriminante des Trinoms stellen wir fest, dass das Trinom keine Nullstellen hat, da das Ergebnis negativ ist. Es gibt also nur eine Lösung.
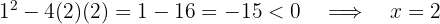
3
Wir wenden das Horner-Schema an, da es sich um eine Gleichung 3. Grades handelt. Die Divisoren von  sind
sind  Somit:
Somit:

Die Faktorisierung ist also  Wir lösen die quadratische Gleichung mit der abc-Formel:
Wir lösen die quadratische Gleichung mit der abc-Formel:
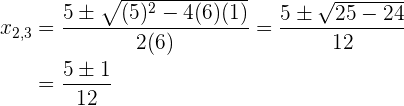
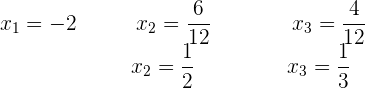
6Löse die folgenden Gleichungssysteme: 
1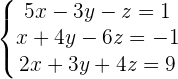
Wir bilden die zum System gehörende Koeffizientenmatrix und lösen.
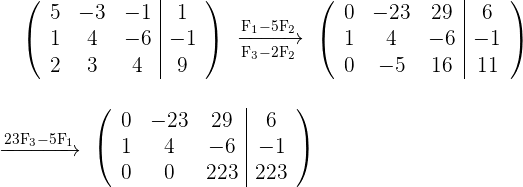
Somit ist 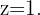 Übertragen wir die letzte Matrix in das dazugehörige Gleichungssystem, erhalten wir
Übertragen wir die letzte Matrix in das dazugehörige Gleichungssystem, erhalten wir  und somit:
und somit:
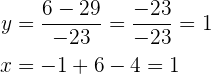
2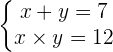
Wir bestimmen eine Unbekannte der ersten Gleichung und setzen den resultierenden Ausdruck in die zweite ein. Danach lösen wir die quadratische Gleichung.
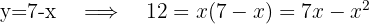
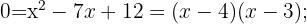

3
Wir bestimmen eine Unbekannte der ersten Gleichung und setzen den resultierenden Ausdruck in die zweite ein. Danach lösen wir die quadratische Gleichung.
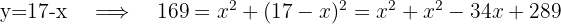


4
Wir setzen den Ausdruck, der für  steht, in die zweite Gleichung ein. Danach quadrieren wir beide Glieder der Gleichung und lösen.
steht, in die zweite Gleichung ein. Danach quadrieren wir beide Glieder der Gleichung und lösen.
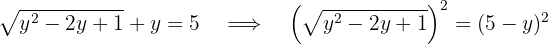


7Bestimme den Wert für  , sodass die Lösungen der Gleichung
, sodass die Lösungen der Gleichung  denselben Wert haben.
denselben Wert haben.
Wir berechnen die Diskriminante und setzen gleich null. Wir erhalten somit eine doppelte Nullstelle.
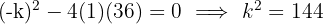
Die möglichen Werte für den Koeffizienten des linearen Terms sind 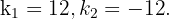
8Bestimme den Wert von zwei Zahlen, deren Summe fünf, und das Produkt dieser Zahlen 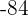 ist.
ist.

Die Zahlenpaare sind  und
und  .
.
9Bestimme das Alter von Peter, wobei du weißt, dass er in  Jahren die Hälfte des Quadrats seines Alters von vor
Jahren die Hälfte des Quadrats seines Alters von vor  Jahren alt sein wird.
Jahren alt sein wird.
 ist sein tatsächliches Alter. Vor
ist sein tatsächliches Alter. Vor  Jahren war er
Jahren war er 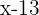 Jahre alt und in
Jahre alt und in  wird der
wird der  Jahre alt sein:
Jahre alt sein: 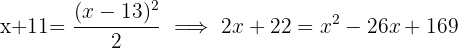

Peter ist  Jahre alt.
Jahre alt.
10Um ein rechteckiges Grundstück mit  einzuzäunen, wurden
einzuzäunen, wurden 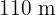 Maschendrahtzaun verwendet. Berechne die Maße des Grundstücks.
Maschendrahtzaun verwendet. Berechne die Maße des Grundstücks.
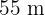 . Hierzu können wir das Problem mit einer Zeichnung wie folgt darstellen:
. Hierzu können wir das Problem mit einer Zeichnung wie folgt darstellen: 

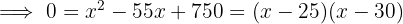
Das Grundstück hat die Maße 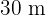 und
und 
11Die drei Seiten eines rechtwinkligen Dreiecks sind proportional zu den Zahlen 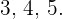 Berechne die Länge jeder Seite des Dreiecks, wenn du weißt, dass es eine Fläche von
Berechne die Länge jeder Seite des Dreiecks, wenn du weißt, dass es eine Fläche von 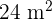 hat.
hat.
 . Mithilfe der Formel zur Berechnung der Fläche kann dieser Faktor ermittelt werden.
. Mithilfe der Formel zur Berechnung der Fläche kann dieser Faktor ermittelt werden. 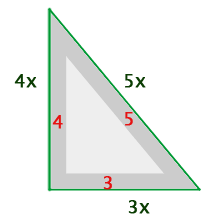
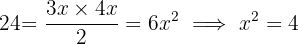
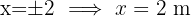
Die Seiten des Dreiecks sind 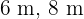 und
und 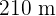 lang.
lang.
12Ein rechteckiger Garten ist 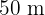 lang und
lang und  breit. Er ist von einem Sandweg mit einer einheitlichen Breite umgeben. Berechne die Breite des Weges, wenn du weißt, dass er eine Fläche von
breit. Er ist von einem Sandweg mit einer einheitlichen Breite umgeben. Berechne die Breite des Weges, wenn du weißt, dass er eine Fläche von 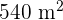 hat.
hat.
 des Sandweges, ergibt sich ein größeres Rechteck mit den Maßen
des Sandweges, ergibt sich ein größeres Rechteck mit den Maßen 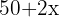 mal
mal  , wie in der Abbildung zu sehen ist. Wir erhalten die Fläche des Sandweges.
, wie in der Abbildung zu sehen ist. Wir erhalten die Fläche des Sandweges. 

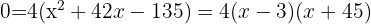
Der Weg ist also 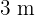 breit.
breit.
13Berechne die Maße eines Rechtecks, dessen Diagonale 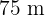 misst, wobei du weißt, dass es ähnlich zu einem Rechteck mit den Maßen
misst, wobei du weißt, dass es ähnlich zu einem Rechteck mit den Maßen 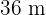 mal
mal 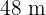 ist.
ist.
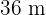 mal
mal 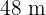 ähnlich ist zu dem Rechteck mit den Maßen
ähnlich ist zu dem Rechteck mit den Maßen 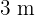 mal
mal 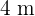 , gilt dies auch für das Rechteck, dessen Diagonale
, gilt dies auch für das Rechteck, dessen Diagonale 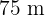 misst. Wir nehmen also an, dass seine Seiten proportional mal einen Faktor
misst. Wir nehmen also an, dass seine Seiten proportional mal einen Faktor  sind, wie die Abbildung zeigt. Wir wenden den Satz des Pythagoras an und berechnen den Wert der Variable.
sind, wie die Abbildung zeigt. Wir wenden den Satz des Pythagoras an und berechnen den Wert der Variable. 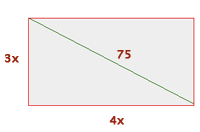
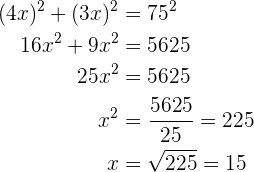
Das Rechteck ist also 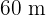 lang und
lang und 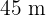 breit.
breit.
14Bestimme eine ganze Zahl, wobei du weißt, dass die Summe mit ihrem Kehrwert 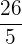 ist.
ist.


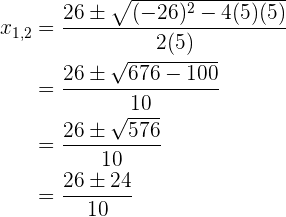
Die Zahl ist 5, da die zweite Wurzel einen Bruch ergibt.
15Berechne zwei natürliche Zahlen, deren Differenz zwei ist und deren Summe der Quadrate 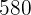 ist.
ist.
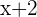 , wenn
, wenn  für eine Zahl steht.
für eine Zahl steht. 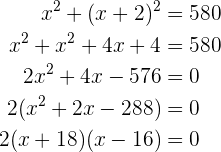
Die Zahlen sind  und
und 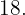
16Zwei Schläuche A und B füllen zusammen einen Pool in 2 Stunden. A schafft es allein in 3 Stunden weniger als B. Berechne, wie viele Stunden jeder von ihnen braucht, um das Becken zu füllen.
 Stunden zum Befüllen des Pools benötigt, benötigt Schlauch B
Stunden zum Befüllen des Pools benötigt, benötigt Schlauch B  Stunden. Somit befüllt A pro Stunde
Stunden. Somit befüllt A pro Stunde  des Pools und B befüllt
des Pools und B befüllt 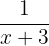 . Da zur vollständigen Befüllung beide Schläuche verwendet werden, gilt:
. Da zur vollständigen Befüllung beide Schläuche verwendet werden, gilt: 
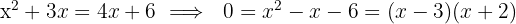
Schlauch A benötigt  Stunden und Schlauch B
Stunden und Schlauch B  Stunden.
Stunden.
17Finde zwei Zahlen, deren Produkt 4 und die Summe ihrer Quadrate 17 ist.
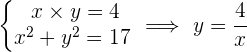

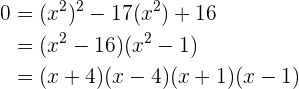
Die möglichen Zahlenpaare sind 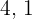 und
und 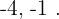
18Bestimme einen Bruch, der  entspricht und dessen Terme zum Quadrat die Summe
entspricht und dessen Terme zum Quadrat die Summe 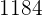 ergeben.
ergeben.
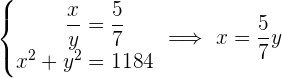
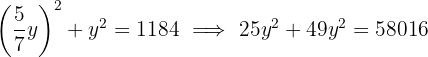

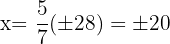
Der Bruch, der die Bedingungen erfüllt, ist  , da die negativen Vorzeichen bei
, da die negativen Vorzeichen bei 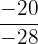 wegfallen und wir den ersten Bruch erhalten.
wegfallen und wir den ersten Bruch erhalten.
19Ein Kunde bezahlt in einem Supermarkt ingesamt 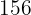 Euro für
Euro für  l Milch,
l Milch,  kg Schinken und
kg Schinken und  l Olivenöl. Berechne den Preis jedes Artikels, wenn du weißt, dass ein Liter Olivenöl dreimal so viel kostet wie ein Liter Milch. Ein kg Schinken kostet genauso viel wie
l Olivenöl. Berechne den Preis jedes Artikels, wenn du weißt, dass ein Liter Olivenöl dreimal so viel kostet wie ein Liter Milch. Ein kg Schinken kostet genauso viel wie  l Olivenöl plus
l Olivenöl plus  l Milch.
l Milch.
 sind der jeweilige Preis für Milch, Schinken und Ölivenöl. Wir stellen ein entsprechendes Gleichungssystem auf und lösen.
sind der jeweilige Preis für Milch, Schinken und Ölivenöl. Wir stellen ein entsprechendes Gleichungssystem auf und lösen. 
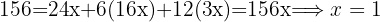

Die Milch kostet 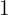 Euro pro Liter, der Schinken
Euro pro Liter, der Schinken  Euro pro kg und das Olivenöl
Euro pro kg und das Olivenöl  Euro pro Liter.
Euro pro Liter.
20Eine Videothek ist auf drei Arten von Filmen spezialisiert: Kinderfilme, amerikanische Western und Horror. Es ist bekannt, dass:
 der Kinderfilme plus
der Kinderfilme plus 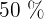 der Westernfilme machen
der Westernfilme machen  der gesamten Filme aus.
der gesamten Filme aus.
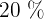 der Kinderfilme plus
der Kinderfilme plus  der Westernfilme plus
der Westernfilme plus  der Horrorfilme machen die Hälfte der gesamten Filme aus.
der Horrorfilme machen die Hälfte der gesamten Filme aus.
Bestimme die Anzal der Filme des jeweiligen Genres, wobei bekannt ist, dass es  mehr Westernfilme als Kinderfilme gibt.
mehr Westernfilme als Kinderfilme gibt.
 sind jeweils die Kinderfilme, die Westernfilme und die Horrorfilme. Wir bilden das entsprechende Gleichungssystem und lösen.
sind jeweils die Kinderfilme, die Westernfilme und die Horrorfilme. Wir bilden das entsprechende Gleichungssystem und lösen. 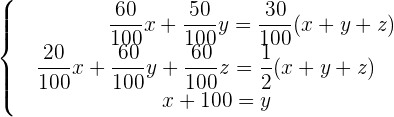
Wir vereinfachen das Gleichungssystem
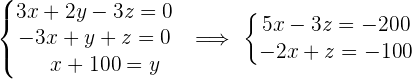
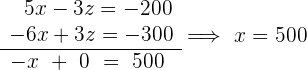
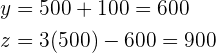
Die Videothek hat  Kinderfilme,
Kinderfilme,  Westernfilme und
Westernfilme und 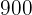 Horrorfilme.
Horrorfilme.
Mit KI zusammenfassen:



