Kapitel

Problemstellung bei der Bewegung von Fahrzeugen
Um Aufgaben zu lösen, bei denen sich Fahrzeuge mit konstanter Geschwindigkeit fortbewegen, werden die Formeln der gleichförmigen Bewegung angewendet:
Strecke = Geschwindigkeit × Zeit
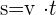
Hierbei gibt es 3 unterschiedliche Problemstellungen:
1. Die Fahrzeuge bewegen sich in die entgegengesetzte Richtung

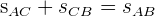
Die vom ersten Fahrzeug bis zum Treffpunkt zurückgelegte Strecke plus der vom zweiten Fahrzeug zurückgelegten Strecke ist gleich deren Entfernung zueinander.
Beispiel:
Zwei Städte  und
und  liegen
liegen 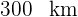 voneinander entfernt. Um 09:00 Uhr morgens verlässt ein Auto die Stadt
voneinander entfernt. Um 09:00 Uhr morgens verlässt ein Auto die Stadt  in Richtung Stadt
in Richtung Stadt  mit einer Geschwindigkeit von
mit einer Geschwindigkeit von  . Von der Stadt
. Von der Stadt  fährt ein anderes Auto in Richtung Stadt
fährt ein anderes Auto in Richtung Stadt  mit einer Geschwindigkeit von
mit einer Geschwindigkeit von  . Ermittle die Zeit, die sie brauchen, bis sie aufeinandertreffen sowie die Uhrzeit des Zusammentreffens und die jeweils zurückgelegte Strecke.
. Ermittle die Zeit, die sie brauchen, bis sie aufeinandertreffen sowie die Uhrzeit des Zusammentreffens und die jeweils zurückgelegte Strecke.
Zeit bis zum Aufeinandertreffen
1 Wir wissen, mit welcher Geschwindigkeit jedes Auto fährt. Wir setzen in die Formel ein und erhalten
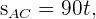
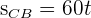
2 Wir wissen, dass die vom ersten Auto zurückgelegte Strecke plus die vom zweiten Auto zurückgelegte Strecke gleich 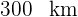 ist
ist
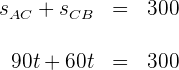
3 Wir lösen die vorhergehende Gleichung
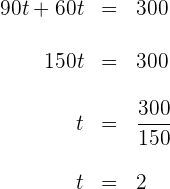
Die Autos treffen nach 2 Stunden aufeinander.
Die Uhrzeit des Aufeinandertreffens
Sie werden um 11:00 Uhr aufeinandertreffen, da sie um 09:00 Uhr losfahren und nach 2 Stunden aufeinandertreffen.
Strecke, die jedes Fahrzeug zurücklegt
Um die Strecke, die jedes Auto zurücklegt, berechnen zu können, setzen wir die Zeit 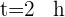 in die Formel ein
in die Formel ein
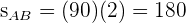
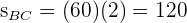
So erfahren wir, dass das erste Auto 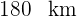 zurücklegt und das zweite Auto
zurücklegt und das zweite Auto 
2. Die Fahrzeuge bewegen sich in dieselbe Richtung

Die vom ersten Fahrzeug zurückgelegte Strecke abzüglich der vom zweiten Fahrzeug zurückgelegten Strecke ist gleich der Distanz zwischen ihnen.
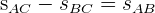
Beispiel:
Zwei Städte  und
und  liegen
liegen 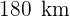 voneinander entfernt. Um 09:00 Uhr morgens verlässt ein Auto jede Stadt und beide Autos fahren in dieselbe Richtung. Das Auto, das Stadt
voneinander entfernt. Um 09:00 Uhr morgens verlässt ein Auto jede Stadt und beide Autos fahren in dieselbe Richtung. Das Auto, das Stadt  verlässt, fährt mit
verlässt, fährt mit  und das Auto, das Stadt
und das Auto, das Stadt  verlässt, fährt mit
verlässt, fährt mit  . Ermittle die Zeit, die sie brauchen, bis sie aufeinandertreffen sowie die Uhrzeit des Zusammentreffens und die jeweils zurückgelegte Strecke.
. Ermittle die Zeit, die sie brauchen, bis sie aufeinandertreffen sowie die Uhrzeit des Zusammentreffens und die jeweils zurückgelegte Strecke.
Zeit bis zum Aufeinandertreffen
1 Wir wissen, mit welcher Geschwindigkeit jedes Auto fährt. Wir setzen in die Formel ein und erhalten
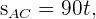
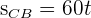
2 Wir wissen, dass die vom ersten Auto zurückgelegte Strecke minus die vom zweiten Auto zurückgelegte Strecke gleich 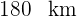 ist
ist
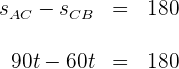
3 Wir lösen die vorhergehende Gleichung
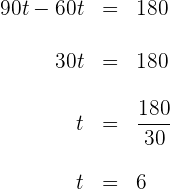
Es dauert 6 Stunden, bis sie aufeinandertreffen.
Die Uhrzeit des Aufeinandertreffens
Sie treffen um 15:00 Uhr aufeinander, da sie um 09:00 Uhr losfahren und es 6 Stunden bis zum Aufeinandertreffen dauert.
Die von jedem Auto zurückgelegte Strecke
Um die von jedem Auto zurückgelegte Strecke zu ermitteln, setzen wir die Zeit 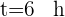 in die Formel ein:
in die Formel ein: 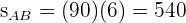 ,
, 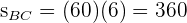 . So ermitteln wir, dass das erste Auto
. So ermitteln wir, dass das erste Auto 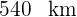 und das zweite
und das zweite 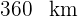 zurücklegt
zurücklegt
3. Die Fahrzeuge starten am selben Punkt und fahren in dieselbe Richtung
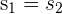
Die vom ersten Fahrzeug zurückgelegte Strecke ist gleich der vom zweiten Fahrzeug zurückgelegten Strecke.
Beispiel:
Ein Auto verlässt die Stadt  mit einer Geschwindigkeit von
mit einer Geschwindigkeit von 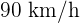 . Drei Stunden später verlässt ein anderes Auto dieselbe Stadt und verfolgt das erste Auto mit einer Geschwindgkeit von
. Drei Stunden später verlässt ein anderes Auto dieselbe Stadt und verfolgt das erste Auto mit einer Geschwindgkeit von 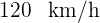 . Ermittle, wie lange das zweite Auto benötigt, bis es das erste Auto einholt sowie die Entfernung, in der das Aufeinandertreffen stattfindet.
. Ermittle, wie lange das zweite Auto benötigt, bis es das erste Auto einholt sowie die Entfernung, in der das Aufeinandertreffen stattfindet.
Die Zeit, bis das zweite Auto das erste Auto einholt.
1 Wenn die Zeit, die das erste Auto benötigt  ist, ist
ist, ist  die Zeit, die das Auto benötigt, das drei Stunden später losfährt.
die Zeit, die das Auto benötigt, das drei Stunden später losfährt.
Wir setzen in die Formel ein und erhalten
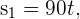
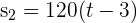
2 Wir wissen, dass beide Autos dieselbe Strecke zurücklegen
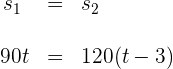
3 Wir lösen die vorhergehende Gleichung
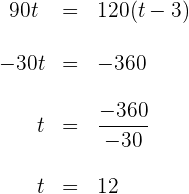
Das erste Auto benötigt  .
.
Das zweite Auto benötigt 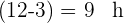 .
.
Die Entfernung, in der sie aufeinandertreffen.
Wir berechnen die von einem der beiden Autos zurückgelegte Strecke
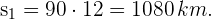
Mit KI zusammenfassen:













