Das Gauß-Verfahren (auch: Gaußsches Eliminationsverfahren) ist ein Additionsverfahren, bei dem mehrere Variablen eliminiert werden, sodass ein LGS in Stufenform (Dreiecksform) entsteht. Dabei bleibt die erste Gleichung unverändert stehen. Alle darauffolgenden Gleichungen enthalten jeweils eine Variable weniger als die vorhergehende.
Im Folgenden lösen wir ein LGS mit drei Gleichungen und drei Variablen Schritt für Schritt nach dem Gauß-Verfahren.
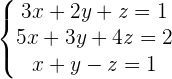
1 Als erste Gleichung nehmen wir die, deren Koeffizient von 
 oder
oder  beträgt. Sollte das nicht gehen, nehmen wir die mit
beträgt. Sollte das nicht gehen, nehmen wir die mit  oder
oder  und tauschen die Reihenfolge der Variablen aus.
und tauschen die Reihenfolge der Variablen aus.

2 Wir führen das Reduktionsverfahren mit der 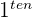 und
und 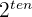 Gleichung durch, um den Term mit
Gleichung durch, um den Term mit  aus der
aus der 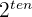 Gleichung zu entfernen. Als zweite Gleichung schreiben wir das Ergebnis aus der Reduktion auf:
Gleichung zu entfernen. Als zweite Gleichung schreiben wir das Ergebnis aus der Reduktion auf:
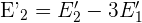
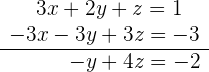
3 Dasselbe machen wir mit der 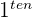 und
und 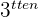 Gleichung, um den Term mit
Gleichung, um den Term mit  zu entfernen.
zu entfernen.
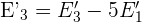


4 Nun nehmen wir die 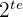 und
und 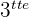 Gleichung in umgewandelter Form und vereinfachen sie, um so den Term mit
Gleichung in umgewandelter Form und vereinfachen sie, um so den Term mit  zu entfernen.
zu entfernen.
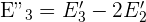
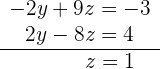
5 Wir erhalten ein LGS in Stufenform.
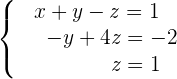
6 Als Lösungen erhalten wir:

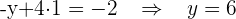
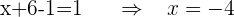
Mit KI zusammenfassen:



