
Überblick über die a-b-c-Formel
Um vorgegebene Aufgaben zu lösen, wird die a-b-c-Formel für Gleichungen zweiten Grades verwendet:

Diese Formel wird verwendet, um eine Gleichung zweiten Grades vom folgenden Typ zu lösen
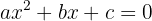 wobei
wobei 
Die Anwendung dieser Methode ist sehr einfach, da wir die Gleichungen nur null setzen müssen und die Werte für a, b, c in die a-b-c-Formel einsetzen müssen.
Beim Lösen einer Gleichung zweiten Grades können 3 Dinge auftreten:
- Es gibt 2 Werte für die Variable x, die die Gleichung erfüllen.
- Es gibt eine einzige Lösung.
- Die Lösung gehört nicht zum System der reellen Zahlen.
Übungsaufgaben zu quadratischen Gleichungen

1 Wir ermitteln die Werte für a, b und c

2 Wir setzen in die a-b-c-Formel ein und lösen





3 Die Gleichung hat zwei verschiedene reelle Lösungen


1 Wir ermitteln die Werte für a, b und c

2 Wir setzen in die a-b-c-Formel ein und lösen





3 Die Gleichung hat zwei verschiedene reelle Lösungen


1 Wir ermitteln die Werte für a, b und c

2 Wir setzen in die a-b-c-Formel ein und lösen





3 Die Gleichung hat zwei verschiedene reelle Lösungen

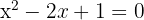
1 Wir ermitteln die Werte für a, b und c

2 Wir setzen in die a-b-c-Formel ein und lösen


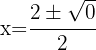


3 Die Gleichung hat nur eine reelle Lösung


1 Wir ermitteln die Werte für a, b und c

2 Wir setzen in die a-b-c-Formel ein und lösen




3 Die Gleichung hat keine reelle Zahl als Lösung.

1 Wir ermitteln die Werte für a, b und c

2 Wir setzen in die a-b-c-Formel ein und lösen





3 Die Gleichung hat nur eine reelle Lösung.


1 Wir bringen alle Terme auf eine Seite der Gleichung, um folgende Form zu erhalten 

2 Wir ermitteln die Werte für a, b und c

3 Wir setzen in die a-b-c-Formel ein und lösen





4 Die Gleichung hat nur eine reelle Lösung.


1 Wir lösen das Binom zum Quadrat

2 Wir bringen alle Terme auf eine Seite und ordnen sie, um die Gleichung in folgender Form darzustellen 

3 Wir ermitteln die Werte für a, b und c

4 Wir setzen in die a-b-c-Formel ein und lösen
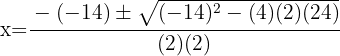




5 Die Gleichung hat zwei reelle Lösungen.


1 In diesem Fall können wir beide Seiten der Gleichung zur Vereinfachung durch 7 dividieren

2 Wir ermitteln die Werte für a, b und c

3 Wir setzen in die a-b-c-Formel ein und lösen





4 Die Gleichung hat zwei reelle Lösungen.


1 Wir multiplizieren beide Seiten mit -1, um eine Gleichung mit a > 0 zu erhalten


2 Die Gleichung hat keine reellen Lösungen

1 Wir wenden das Distributivgesetz an, um die Klammer aufzulösen und erhalten:

2 Wir bringen alle Terme auf die linke Seite der Gleichung

3 Wir ermitteln die Werte für a, b und c

4 Wir setzen in die a-b-c-Formel ein und lösen





5 Die Gleichung hat zwei reelle Lösungen.


1 Wir ermitteln die Werte für a, b und c

2 Wir setzen in die a-b-c-Formel ein und lösen





3 Die Gleichung hat zwei verschiedene reelle Lösungen
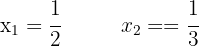

1 Wir lösen das Binom zum Quadrat

2 Wir bringen alle Terme auf eine Seite und ordnen sie, um die Gleichung wie folgt darzustellen 

3 Wir dividieren beide Seiten zur Vereinfachung durch 2

4 Wir ermitteln die Werte für a, b und c

5 Wir setzen in die a-b-c-Formel ein und lösen





6 Die Gleichung hat zwei reelle Lösungen.


1 Wir ermitteln die Werte für a, b und c

2 Wir setzen in die a-b-c-Formel ein und lösen





3 Die Gleichung hat zwei verschiedene reelle Lösungen


1 Wir ermitteln die Werte für a, b und c

2 Wir setzen in die a-b-c-Formel ein und lösen





3 Die Gleichung hat zwei verschiedene reelle Lösungen


1 Wir multiplizieren die linke Seite der Gleichung mit 6 und die rechte Seite der Gleichung mit 2, um den Nenner (6) zu entfernen und erhalten somit:

2 Wir ermitteln die Werte für a, b und c

3 Wir setzen in die a-b-c-Formel ein und lösen





4 Die Gleichung hat zwei reelle Lösungen.

Mit KI zusammenfassen:













