Kapitel
Eine Gleichung zweiten Grades hat folgende Form:
 mit
mit 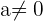
Man löst sie anhand der folgenden allgemeinen Formel:

Allgemeine Formel zur Berechnung von Gleichungen zweiten Grades
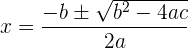
Der Teil innerhalb der Wurzel  ist die Diskriminante. Über sie erfahren wir wichtige Informationen zur Lösung unserer Gleichung.
ist die Diskriminante. Über sie erfahren wir wichtige Informationen zur Lösung unserer Gleichung.
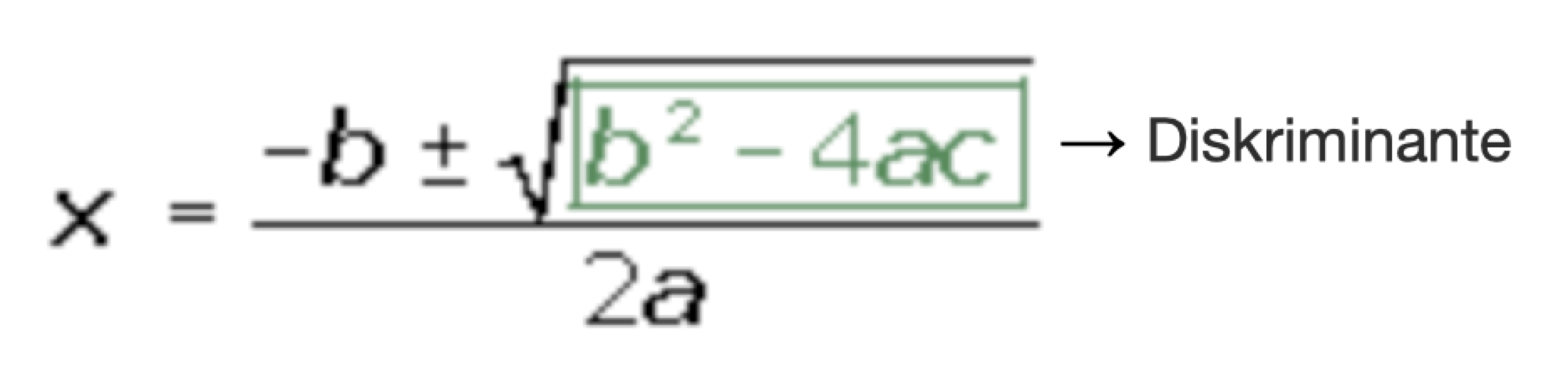
An der Diskriminante können wir die Nummer der Lösungen für jede Gleichung ablesen. Diese drei Fälle werden dabei unterschieden:
1
Wenn die Diskriminante positiv ist, d.h. wenn 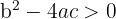 , besitzt die Gleichung zweiten Grades 2 mögliche Lösungen in Form von zwei unterschiedlichen reellen Zahlen.
, besitzt die Gleichung zweiten Grades 2 mögliche Lösungen in Form von zwei unterschiedlichen reellen Zahlen.
2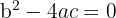
Wenn die Diskriminante gleich Null ist, d.h. wenn 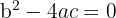 , besitzt die Gleichung zweiten Grades eine doppelte Lösung.
, besitzt die Gleichung zweiten Grades eine doppelte Lösung.
3
Wenn die Diskriminante negativ ist, d.h.  ,besitzt die Gleichung zweiten Grades keine reelle Zahl als Lösung.
,besitzt die Gleichung zweiten Grades keine reelle Zahl als Lösung.
Eigenschaften der Lösungen von Gleichungen zweiten Grades
Die Summe der Lösungen einer Gleichung zweiten Grades ist gleich:

Das Produkt der Lösungen einer Gleichung zweiten Grades ist gleich:

Gleichungen zweiten Grades auf Basis der Lösungen erstellen
Wenn uns die Wurzeln einer Gleichung zweiten Grades bekannt sind, können wir die Gleichung auf folgende Weise notieren:
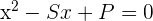
Dabei sind
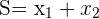
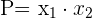
Beispiel:
Erstelle eine Gleichung zweiten Grades, deren Lösungen folgende sind:  und
und  .
.


Die Gleichung ist:
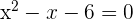
Faktorisierung eines Trinoms zweiten Grades
Gegeben sei eine vollständige Gleichung zweiten Grades:

Sie kann wie folgt in einzelne Faktoren zerlegt werden:
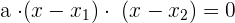
Beispiel

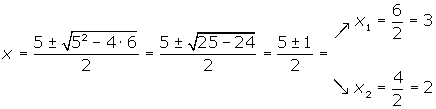

Beispielaufgaben zu Gleichungen zweiten Grades
1 
In diesem Fall können wir feststellen, dass:
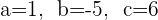
Wir wenden die Formel an:
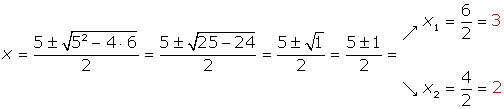
2 
In diesem Fall können wir feststellen, dass:
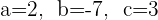
Wir wenden die Formel an:
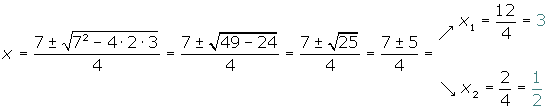
3 
Wenn  , multiplizieren wir beide Seiten mit
, multiplizieren wir beide Seiten mit  .
.


Wir stellen fest, dass:

Wir wenden die Formel an:
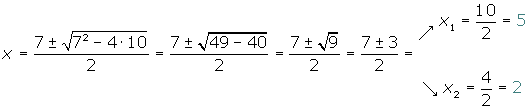
Mit KI zusammenfassen:













