Kapitel

Einsetzungsverfahren für LGS
Das Einsetzungsverfahren besteht, wie sein Name sagt, darin, den Wert einer der beiden Gleichungen eines linearen Gleichungssystems (LGS) die andere Gleichung einzusetzen.
ANMERKUNG
Wenn ein LGS mehr Variablen (Unbekannte) als Anzahl an Gleichungen enthält, besitzt es unendlich viele Lösungen, d.h. jede Variable kann unterschiedliche Werte annehmen, anhand derer die Gleichung aufgeht. Jede Variable kann unendlich viele Lösungen einnehmen. Beispiel:
Gegeben sei die Gleichung 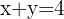 Es handelt sich um eine Gleichung mit zwei Variablen. Wir können schnell einige Werte erkennen, für welche die die Gleichung aufgeht:
Es handelt sich um eine Gleichung mit zwei Variablen. Wir können schnell einige Werte erkennen, für welche die die Gleichung aufgeht:
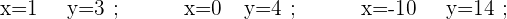

Man sieht, dass es unendlich viele Werte für  und
und  gibt, mit denen die Gleichung aufgeht.
gibt, mit denen die Gleichung aufgeht.
Wenn also anders herum ein LGS genauso viele Gleichungen wie Unbekannte besitzt, gibt es in der Regel eine einzige Lösung.
Einsetzungsverfahren - Beispiel: LGS mit 2 Gleichungen und 2 Unbekannten
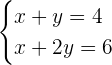
A 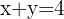 bezeichnen wir als "Gleichung I"
bezeichnen wir als "Gleichung I"
y  bezeichnen wir als "Gleichung II"
bezeichnen wir als "Gleichung II"
Löse nach einer beliebigen Variable in einer beliebigen Gleichung auf. Nimm dabei immer die Variable, die den geringsten Rechenaufwand verursacht. In diesem Fall bietet es sich an, nach  in Gleichung I aufzulösen:
in Gleichung I aufzulösen:
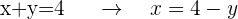
Du erhältst den "Wert von  in Bezug auf
in Bezug auf  "
"
Setze den erhaltenen Wert in die andere Gleichung ein. In diesem Fall setzt du also den Wert von  in die Gleichung II ein:
in die Gleichung II ein:
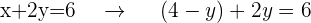
Die Gleichung enthält nun nur die Variable  . Vereinfache die Gleichung, sodass ein exakter Wert für
. Vereinfache die Gleichung, sodass ein exakter Wert für  dasteht.
dasteht.
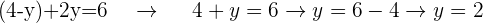
Sobald du den Wert für eine der Variablen ermittelt hast (in diesem Fall von  ), kannst du ihn in eine der beiden anderen Gleichungen einsetzen, um den Wert der anderen Variable zu ermitteln (in diesem Fall von
), kannst du ihn in eine der beiden anderen Gleichungen einsetzen, um den Wert der anderen Variable zu ermitteln (in diesem Fall von  ).
).
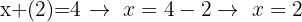
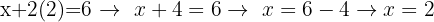
Du kannst dafür auch direkt die Gleichung verwenden, die du beim Auflösen nach x erhalten hast, da du so am schnellsten den Wert von x erhältst:
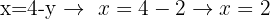
So kannst du die Werte von Variablen eines LGS mit einer einzigen Lösung einfach berechnen.
Rechenschritte zur Lösung von LGS mit 3 Unbekannten
1 Eine Variable auswählen und nach ihr in einer der Gleichungen auflösen:
In der Regel nimmt man die Variable mit dem kleinsten Koeffizienten aus der einfachsten Gleichung, um sich unnötige Rechenarbeit zu sparen.
2 Den Wert in die anderen Gleichungen einsetzen:
Nutze den Wert, den du beim Auflösen erhalten hast, um ihn in die anderen beiden Gleichungen einzusetzen. Die beiden neuen Gleichungen, die du beim Einsetzen erhältst, bilden ein neues LGS mit zwei Gleichungen.
3 LGS auflösen:
Wiederhole dafür den Vorgang:
- Wähle einer der beiden Variablen aus und löse nach ihr in einer der Gleichungen auf.
- Setze den erhaltenen Wert in die andere Gleichung des neuen LGS ein.
- Du erhältst eine lineare Gleichung mit einer Variablen und erhältst ihren Wert, indem du nach ihr auflöst.
- Setze den erhaltenen Wert in die andere Gleichung des neuen LGS ein, um den Wert der zweiten Variable zu erhalten.
4 Die noch fehlende Variable ermitteln:
Da du bei Schritt 3 die Werte von 2 der Variablen erhalten hast, setzt du diese nun in die Gleichung des ursprünglichen LGS ein, in dem du nach der ersten Variablen aufgelöst hast.
Gemischte Aufgaben


Um das Einsetzungsverfahren anzuwenden, wähle eine Gleichung und eine Variable aus, nach der du auflösen willst. Da das Auflösen so einfach wie möglich sein sollte, bietet es sich an, die dritte Gleichung zu nehmen, die den kleinsten Koeffizienten hat, und nach  aufzulösen
aufzulösen

Setze den Wert, den du beim Auflösen erhalten hast, in die anderen beiden Gleichungen ein.








Du erhältst ein neues LGS mit 2 Gleichungen

Hier muss wieder das Einsetzungsverfahren angewendet werden, d.h. nach einer Variablen in einer der Gleichungen aufgelöst werden. Diesmal bietet sich  als einfachste Option an.
als einfachste Option an.

Setze den erhaltenen Term in die andere Gleichung ein:




Da wir als Lösung z=1 haben, setze den Wert von z in die letzte Gleichung ein, die beim Auflösen nach y entstanden ist:

Nun fehlt nur noch der Wert von  . Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach x erhalten hast und setze dort die beiden bekannten Werte ein:
. Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach x erhalten hast und setze dort die beiden bekannten Werte ein:
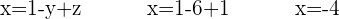


Um das Einsetzungsverfahren anzuwenden, wähle eine Gleichung und eine Variable aus, nach der du auflösen willst. Da das Auflösen so einfach wie möglich sein sollte, bietet es sich an, die zweite Gleichung zu nehmen, die den kleinsten Koeffizienten hat, und nach  aufzulösen
aufzulösen

Setze den Wert, den du beim Auflösen erhalten hast, in die anderen beiden Gleichungen ein.








Du erhältst ein neues LGS mit 2 Gleichungen
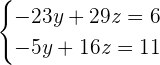
Hier muss wieder das Einsetzungsverfahren angewendet werden, d.h. nach einer Variablen in einer der Gleichungen aufgelöst werden. Diesmal bietet sich  als einfachste Option an.
als einfachste Option an.
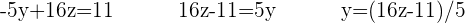
Setze den erhaltenen Term in die andere Gleichung ein: Um den Nenner zu entfernen, multipliziere die Gleichung mit 5:





Da wir als Lösung  haben, setze den Wert von z in die letzte Gleichung ein, die beim Auflösen nach y entstanden ist:
haben, setze den Wert von z in die letzte Gleichung ein, die beim Auflösen nach y entstanden ist:
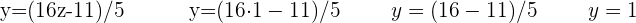
Nun fehlt nur noch der Wert von  . Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach x erhalten hast und setze dort die beiden bekannten Werte ein:
. Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach x erhalten hast und setze dort die beiden bekannten Werte ein:



Um das Einsetzungsverfahren anzuwenden, wähle eine Gleichung und eine Variable aus, nach der du auflösen willst. Da das Auflösen so einfach wie möglich sein sollte, bietet es sich an, die erste Gleichung zu nehmen, die den kleinsten Koeffizienten hat, und nach  aufzulösen
aufzulösen

Setze den Wert, den du beim Auflösen erhalten hast, in die anderen beiden Gleichungen ein.








Du erhältst ein neues LGS mit 2 Gleichungen
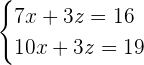
Hier muss wieder das Einsetzungsverfahren angewendet werden, d.h. nach einer Variablen in einer der Gleichungen aufgelöst werden. Diesmal bietet sich  als einfachste Option an.
als einfachste Option an.

Setze den erhaltenen Term in die andere Gleichung ein:







Da wir als Lösung  haben, setze den Wert in die letzte Gleichung ein, die beim Auflösen nach
haben, setze den Wert in die letzte Gleichung ein, die beim Auflösen nach  entstanden ist:
entstanden ist:

Nun fehlt nur noch der Wert von  . Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach y erhalten hast und setze dort die beiden bekannten Werte ein:
. Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach y erhalten hast und setze dort die beiden bekannten Werte ein:
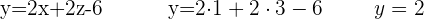
Der Kunde eines Supermarkts hat beim Einkauf  € für
€ für  Milch,
Milch,  Schinken und
Schinken und  Olivenöl bezahlt. Berechne den Preis jedes Produkts, wenn
Olivenöl bezahlt. Berechne den Preis jedes Produkts, wenn  Olivenöl dreimal so viel kostet wie
Olivenöl dreimal so viel kostet wie  Milch
Milch
und  Schinken das gleiche kostet wie
Schinken das gleiche kostet wie  Öl plus
Öl plus  Milch.
Milch.
Lege die Variablen fest:
Milch: 
Schinken: 
Olivenöl: 
Aus jedem Satz der Aufgabenstellung bilden wir nun eine Gleichung und erhalten dabei das folgende LGS:

In diesem Fall stehen die Terme für zwei der Variablen schon fest (Gleichung 2 und 3). Setze den Term von  der zweiten Gleichung in die dritte ein.
der zweiten Gleichung in die dritte ein.
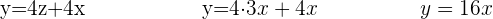
Setze die Werte von  und
und  in die erste Gleichung ein
in die erste Gleichung ein





Verwende die Gleichungen von  und
und  , um ihre Werte zu erhalten
, um ihre Werte zu erhalten

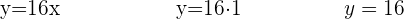
Die Variablen sind also:
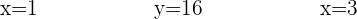
Das heißt, die Preise sind:
Milch 1 €
Schinken 16 €
Olivenöl 3 €
Ein Videoclub hat sich auf den Verleih dreier Arten von Filmen spezialisiert:
Kinderfilme
Wilder Westen
Horrorfilme
Es ist bekannt, dass:
 der Kinderfilme plus
der Kinderfilme plus  der Filme aus dem Wilden Westen
der Filme aus dem Wilden Westen der Filme insgesamt ausmachen.
der Filme insgesamt ausmachen.
 der Kinderfilme plus
der Kinderfilme plus  der Filme aus dem Wilden Westen plus
der Filme aus dem Wilden Westen plus  der
der
Horrorfilme stellen die Hälfte aller Filme im Club dar.
Es gibt  Filme aus dem Wilden Westen mehr als Kinderfilme.
Filme aus dem Wilden Westen mehr als Kinderfilme.
Wie viele Filme aus jedem Genre gibt es im Club?
Ordne jedem Element aus der Aufgabenstellung eine Variable zu.Kinderfilme: 
Wilder Westen: 
Horrorfilme: 
Aus der Aufgabenstellung erhält man das folgende LGS mit drei Gleichungen:

Schreibe die erste Gleichung um und vereinfache sie:

Multipliziere jede Gleichung mit 100, um den Nenner aufzulösen und vereinfache die Gleichung:



Teile durch  und du erhältst:
und du erhältst:

Nimm die zweite Gleichung und führe die folgenden Rechenschritte durch:

Um die Brüche auf denselben Nenner zu bringen, multipliziere den rechten Teil der Gleichung mit  und du erhältst:
und du erhältst:

Entferne den Nenner und vereinfache:


Teile die Gleichung durch  :
:

Verwende die vereinfachten Versionen der ersten und zweiten Gleichung und du erhältst das folgende LGS:

Da eine Variable bereits alleine steht, verwenden wir  für das Einsetzungsverfahren in die ersten ursprünglichen Gleichungen und multiplizieren letztere mit 3.
für das Einsetzungsverfahren in die ersten ursprünglichen Gleichungen und multiplizieren letztere mit 3.








Du erhältst ein neues LGS mit 2 Gleichungen

Hier muss wieder das Einsetzungsverfahren angewendet werden, d.h. nach einer Variablen in einer der Gleichungen aufgelöst werden. Diesmal bietet sich  als einfachste Option an.
als einfachste Option an.

Setze den erhaltenen Term in die andere Gleichung ein:





Da wir als Lösung  haben, setze den Wert in die letzte Gleichung ein, die beim Auflösen nach
haben, setze den Wert in die letzte Gleichung ein, die beim Auflösen nach  entstanden ist:
entstanden ist:

Nun fehlt nur noch der Wert von  . Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach y erhalten hast und setze dort die beiden bekannten Werte ein:
. Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach y erhalten hast und setze dort die beiden bekannten Werte ein:
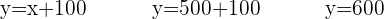
Es gibt also:
Kinderfilme 500
Wilder Westen 600
Horrorfilme 900
Die Seiten eines Dreiecks sind  ,
,  und
und  lang.
lang.
Von den Scheitelpunkten aus wird jeweils ein Umkreis gezeichnet. Jeder Umkreis tangiert die beiden anderen Umkreise.
Berechne die Radien der drei Umkreise.
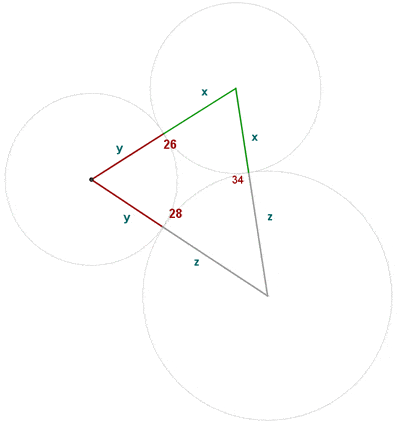
Aus der Skizze der Figur ergibt sich folgendes LGS, wenn man eine Variable für jeden Radius verwendet:
Um das Einsetzungsverfahren anzuwenden, wähle eine Gleichung und eine Variable aus, nach der du auflösen willst. In diesem Fall bietet sich  aus der ersten Gleichung an:
aus der ersten Gleichung an:

Setze den Wert, den du beim Auflösen erhalten hast, in die anderen beiden Gleichungen ein.





In diesem Fall enthält die Gleichung keine Variable x, daher lassen wir sie so stehen.
Man erhält ein neues LGS mit zwei Gleichungen:

Hier muss wieder das Einsetzungsverfahren angewendet werden, d.h. nach einer Variablen in einer der Gleichungen aufgelöst werden. Diesmal bietet sich  als einfachste Option an:
als einfachste Option an:

Setze den erhaltenen Term in die andere Gleichung ein:






Da wir als Lösung  haben, setze den Wert in die letzte Gleichung ein, die beim Auflösen nach
haben, setze den Wert in die letzte Gleichung ein, die beim Auflösen nach  entstanden ist:
entstanden ist:
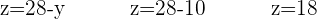
Nun fehlt nur noch der Wert von  . Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach x erhalten hast und setze dort die beiden bekannten Werte ein:
. Gehe dafür zurück zur ersten Gleichung, die du beim Auflösen nach x erhalten hast und setze dort die beiden bekannten Werte ein:
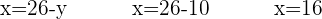
Mit KI zusammenfassen:













