Ein Gleichungssystem ist nichtlinear, wenn mindestens eine der Gleichungen nicht vom Grad 1 ist.
Beispiel:
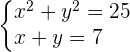
Schritte des Substitutionsverfahrens
Diese Gleichungssysteme werden normalerweise mit dem Substitutionsverfahren gelöst. Hierzu führen wir folgende Schritte durch:
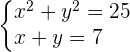
1 Wir bestimmen die Variable in einer der Gleichungen, vorzugweise in der Gleichung vom Grad 1.
2 Wir setzen den erhaltenen Wert in die andere Gleichung ein.
3 Wir lösen die resultierende Gleichung.
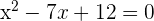
4 Wir setzen jeden der resultierenden Werte in die andere Gleichung ein. Daraus ergeben sich die entsprechenden Werte für die andere Variable.
Aufgaben mit Lösungen zu Gleichungssystemen
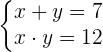
1 Wir bestimmen die Variable der Gleichung vom Grad 1
2 Wir setzen in die andere Gleichung ein
Wir gehen wie folgt vor:
Es handelt sich und eine quadratische Gleichung
3 Wir lösen
Aus der abc-Formel ergibt sich
4 Wir bestimmen den Wert der anderen Variablen
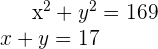
1 Wir bestimmen die Variable der Gleichung vom Grad 1 
2 Wir setzen in die andere Gleichung ein
Wir gehen wie folgt vor:
Es handelt sich um eine quadratische Gleichung
3 Wir lösen
Aus der abc-Formel ergibt sich
4 Wir bestimmen den Wert der anderen Variablen
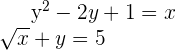
1 Wir bestimmen die Variable einer der Gleichungen
In diesem Fall gibt es keinen Grad 1, allerdings stellen wir fest, dass x bereits in der ersten Gleichung bestimmt ist.
2 Wir setzen in die andere Gleichung ein
Wir sehen uns die Wurzel an
Wir quadrieren
Wir gehen wie folgt vor:
3 Wir lösen
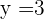
4 Wir bestimmen den Wert der anderen Variablen
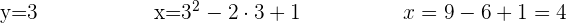
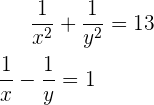
1 Variablentausch
Die ursprüngliche Gleichung sieht nun wie folgt aus
2 Wir bestimmen die Variable einer der Gleichungen
3 Wir setzen in die andere Gleichung ein
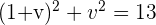
Wir gehen wie folgt vor:
4 Wir lösen
Aus der abc-Formel ergibt sich
5 Wir ermitteln den Wert der anderen Variablen
6 Wir betrachten den Variablentausch, den wir am Anfang durchgeführt haben
Mit der Lösung 
Mit der Lösung 
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
